Graficación
en dos y tres dimensiones.
Graficas
en dos dimensiones.
Suponga
que desea graficar un conjunto de puntos de datos [xi, yi],
i = 1,2,3, ..., n. En necesario hacer
dos arreglos, del mismo tamaño, para x y y que representen los valores que
deseamos graficar. Una manera de hacerlo es utilizando la instrucción plot.
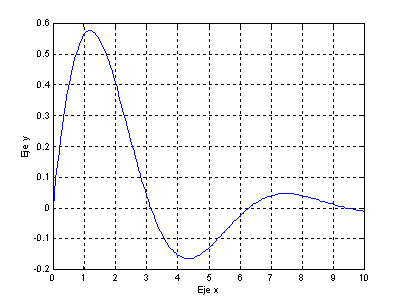
Ejemplo 1.
Graficar
la función f(x)=seno(x)e(-0.4x) para x = [0, 10].
x = 0: 0.05: 10;
y = sin(x).*exp(-0.4*x);
plot(x,y);
xlabel('Eje
x');
ylabel('Eje
y');
grid on;
Los
rótulos de los ejes de imprimen con los comando xlabel y ylabel.
También se
pueden utilizar vectores columna para realizar gráficas.
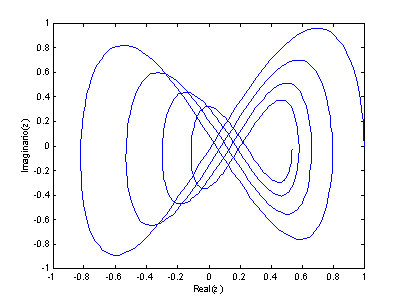
Ejemplo 2.
p= 0: 0.05: 8*pi;
z = (cos(p) +
i*sin(2*p)).*exp(-0.05*p) + 0.01*p;
plot(real(z),
imag(z));
xlabel('Real(z)');
ylabel('Imaginario(z)');
Graficación
utilizando únicamente marcas.
Los datos pueden graficarse solo con marcas sin estar
conectados por líneas. Se dispone de cinco tipos de marcas o letras.
|
Tipo de
marca |
Símbolo |
|
Punto |
. |
Mas |
+ |
|
Estrella |
* |
|
Circulo |
o |
Marca x |
x |
También se pueden utilizar líneas
|
Tipo de
línea |
Símbolo |
|
continua |
- |
|
guiones |
-- |
|
Punteada |
: |
|
Guiones
y puntos |
-. |
y colores.
|
Color de
línea |
Símbolo |
|
rojo |
r |
|
amarillo |
y |
|
magenta |
m |
|
turquesa |
c |
|
verde |
g |
|
azul |
b |
|
blanco |
w |
|
negro |
k |
Es posible
hacer combinaciones de colores y marcas así, por ejemplo:
plot(x,
y, ‘+g’); % grafica una curva utilizando cruces y
color verde.
plot(x,
y, ‘k’); %
grafica en color negro sin marcas
plot(x,
y, ‘-.b’); % grafica en color azul con linea punteda.
Graficación
de funciones con fplot.
Otra forma
de grafica funciones individuales es con fplot.
fplot(‘archivo’, [xmin, xmax]);
donde
archivo es el nombre del archivo que contiene los datos a graficar y [xmin y
xmax] los limites de la función a graficar.
Borrado de
Gráficas.
El comando
clf borra todo lo que haya en la ventana de gráficos, mientras cla borra las
curvas y redibuja los ejes.
Retículas
Se puede
agregar un conjunto de líneas paralelas a los ejes, para hacer mas legible la
lectura de datos en la gráfica, a este conjunto de líneas se le llama retícula.
La instrucción para ponerla es:
grid
on;
Graficas
polares.
Podemos
hacer gráficas en coordenadas polares utilizando la instrucción:
polar(t,
y);
Esta
instrucción es muy similar a plot, la diferencia estriba en que el sistema de
coordenadas ya no es un sistema cartesiano x, y, sino un sistema polar r,
q.
tetha = 0: 0.05: 4*pi+0.1;
r = sin(4*tetha);
polar(tetha, r);
title('Rosa
de ocho hojas');
grid on;
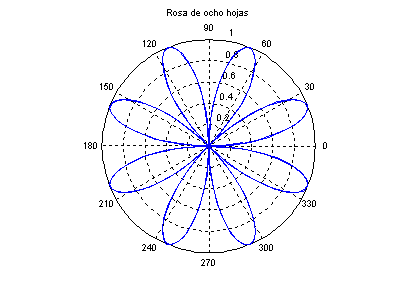
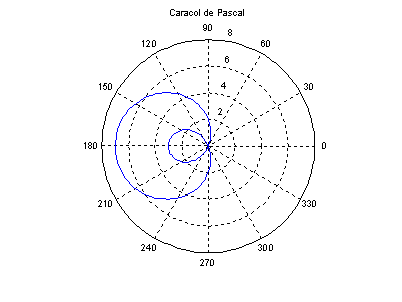
tetha = 0.01: 0.05: 2*pi+0.1;
r = 2-5*cos(tetha);
polar(tetha, r);
title('Caracol
de Pascal');
grid on;
Ejes.
El mínimo y el máximo de los ejes de coordenadas son determinados automáticamente, sin embargo, hay manera de ajustarlos automáticamente utilizando el comando axis.
axis(‘square’);
% redibuja en forma cuadrada.
axis(‘off’);
% cancela el efecto
axis([x_min,
x_max, y_min, ymax]) % establece los valores mínimos y máximos para cada eje.
Gráficas
Logarítmicas y semilogaritmicas.
Las
funciones pueden graficarse en una escala log-log utilizando el comando
loglog(x,y);
y también
podemos representar una curva en una escala semilogarítmica utilizando
semilogx(x,y);
% en la dirección de x
semilogy(x,y);
% en la dirección de y
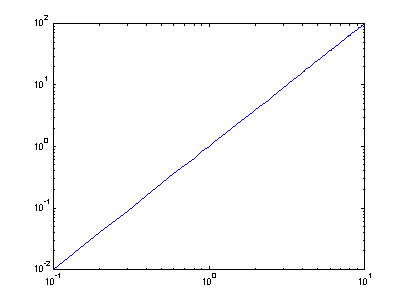
Ejemplo 3.
El
siguiente ejemplo muestra como trazar una función en una escala logarítmica-locarítmica.
x = 0:0.1:10;
y = x.^2;
loglog(x,y);
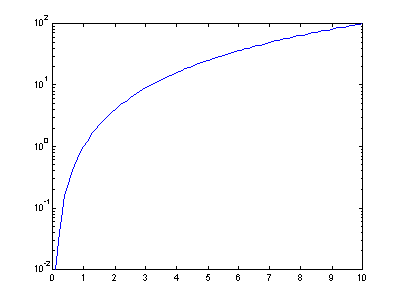
x = 0:0.1:10;
y = x.^2;
%loglog(x,y);
semilogy(x,y);
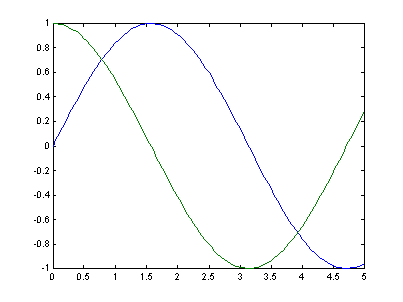
Graficación
de múltiples curvas.
Se uno
desea graficar mas de una curva entonces será necesario en la instrucción plot
poner mas de un par de termino a graficar tal como se muestra a continuación.
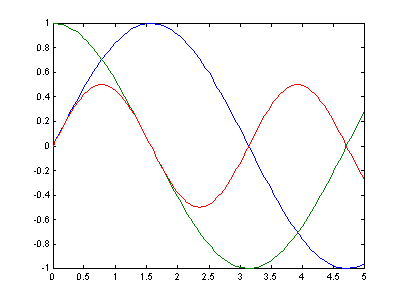
x = 0: 0.05:5;
y = sin(x);
z = cos(x);
plot(x, y, x, z);
Automáticamente se
seleccionaran los colores de cada grafica y si uno desea podrán cambiarse
haciendo
x = 0: 0.05:5;
y = sin(x);
z = cos(x);
plot(x, y, '--', x, z, '*');
En algunos casos
resulta útil mandar a graficar utilizando solo un par de argumentos en la
sentencia plot. En tal caso se procede :
clear;
x = 0: 0.05:5;
y(1, :) = sin(x);
y(2, :) = cos(x);
y(3, :) = sin(x).*cos(x);
plot(x, y);
Retención
(Sobre poner gráficas).
Hasta el
momento hemos realizado el trazado de
las curvas utilizando una sola operación. Pero si deseamos graficar sobre una
grafica ya realizada utilizaremos el comando hold on.
clear;
x = 0: 0.05:5;
y = sin(x);
plot(x, y, 'b*');
hold
on;
z =
cos(x);
plot(x,
z, 'r--');
yz = sin(x).*cos(x);
plot(x,
yz, 'k-.');
Títulos y Leyendas.
Podemos agregar títulos a nuestras gráficas
utilizando la instrucción
title
(‘texto para la grafica’);
y leyendas en cualquier posición con el comando
text(x,
y, ‘cadena’)
donde x y y representa las coordenadas de la gráfica
donde deseas que aparezca impresa la cadena.
Subgráficas.
Con el comando subplot podemos gráficar m por n gráficas
en una sola figura. La sintaxis del comando es
subplot(m, n, k)
donde m y n se refiere al arreglo de graficas y k al
número de grafica sobre al que se trabaja.
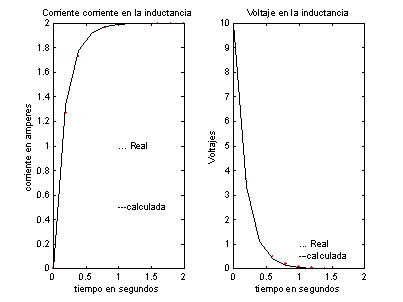
Ejemplo 4.
Calcular el voltaje y corriente transitoria que
circulan por la inductancia de un circuito RL serie. Para encontrar la solución
utilice el método de la regla trapezoidal y compare el resultado con la
solución real.
function y1 = RL1(Tf, inc)
global V R L H
V =
10;
R =
5;
L =
1;
H =
inc;
Ic(1)
= 0;
num_iter
= Tf/inc;
t = 0:inc:Tf;
Ir = (V/R)*(1-exp(-R*t/L));
for iter = 1: num_iter
Ic(iter+1) = f(Ic(iter));
end;
subplot(1,
2, 1);
plot(t,
Ir, '.r');
title('Corriente
corriente en la inductancia');
xlabel('tiempo
en segundos');
ylabel('corriente
en amperes');
hold
on;
plot(t,
Ic, 'k');
text(1,
1, '... Real');
text(1, 0.5, '---calculada');
Vr = V - R*Ir;
Vc =
V - R*Ic;
subplot(1,2,
2);
plot(t,
Vr, '.r');
title('Voltaje
en la inductancia');
xlabel('tiempo
en segundos');
ylabel('Voltajes');
hold
on;
plot(t,
Vc, 'k');
text(1,
1, '... Real');
text(1, 0.5, '---calculada');
hold
off;
function I1 = f(Io)
global V R L
H
I1 = (Io +
(2*V-R*Io)*H/(2*L))/(1+R*H/(2*L));
Gráficas en tres dimensiones.
Una función tridimensional puede ser definido como
una función z = z(x,y) . Una matriz es el mejor ejemplo de una función en
tres dimensiones donde x y y representan los índices del arreglo y z(x,y) el
contenido de la matriz.
Para gráficar una función en tres dimensiones
utilizamos el comando
mesh(z)
El comando mesh(z) desplegara la función contenida en
la matriz z.
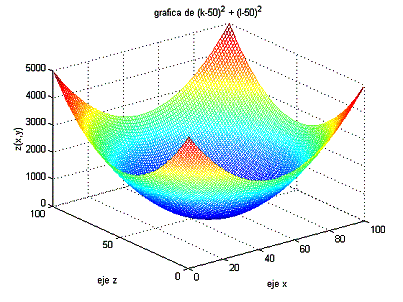
Ejemplo 5.
Trazar la curva de la función f(x,y) = (x-50)2
+ (y-50)2, en el rango x = [1,100] y y =[1,100].
clear;
for k=1:100;
for l=1:100;
z(k,l) = (k-50)^2 + (l-50)^2;
end;
end;
mesh(z);
title ('grafica
de (k-50)^2 + (l-50)^2');
xlabel ('eje x');
ylabel ('eje z');
zlabel ('z(x,y)');
Si deseas únicamente graficar las líneas de contorno se utiliza la
instrucción contour.

clear;
for k=1:100;
for l=1:100;
z(k,l) = (k-50)^2 + (l-50)^2;
end;
end;
contour(z);
title ('grafica
de (k-50)^2 + (l-50)^2');
xlabel ('eje x');
ylabel ('eje y');
zlabel ('z(x,y)');
Malla.
En algunos casos donde los puntos en la dirección de x
y de y no son valores enteros positivos, tenemos que hacer uso del comando
meshgrid.
Ejemplo 6.
Trazar la gráfica de la función z = x*exp(-x2-y2)
en el rango x=[-2,2] y y =[-2,2].
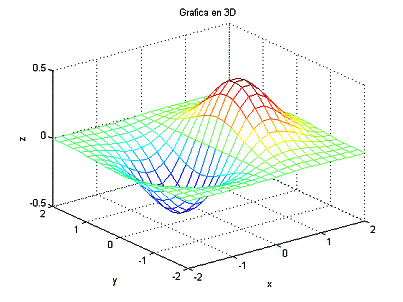
clear,
clf;
xa =
-2:0.2:2;
ya = -2:0.2:2;
[x y] = meshgrid(xa,ya);
z = x.*exp(-x.^2-y.^2);
mesh(x, y, z);
title ('Grafica
en 3D');
xlabel('x');
ylabel('y'); zlabel('z');
Gráfica
Vectorial.
En ocasiones, las cantidades correspondientes a
los puntos de una retícula se dan en forma vectorial. Por ejemplo la
distribución de la velocidad en un flujo, etc. Los vectores en estos puntos
pueden calcularse utilizando el comando quiver y requieren de dos vectores uno
en la dirección de x y otro en la dirección de y.
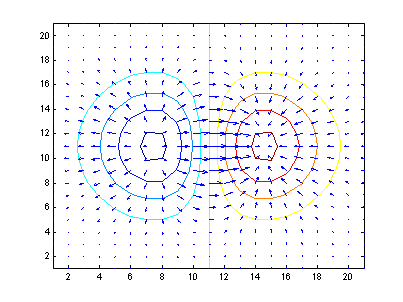
Ejemplo 7.
Graficar el vector gradiente correspondiente a la curva
z = x*exp(-x2-y2).
[x,y] = meshgrid(-2:.2:2,
-2:.2:2);
z = x .* exp(-x.^2 - y.^2);
[px,py]
= gradient(z,.2,.2);
contour(z),hold
on, quiver(px,py), hold off
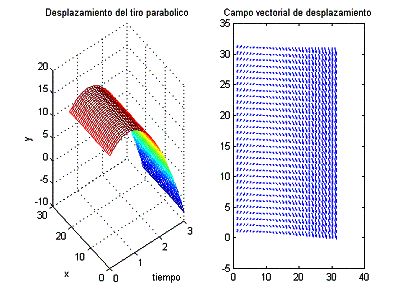
Ejemplo 8.
Determinar la gráfica correspondiente a un tiro parabólico.
clear;
Vo = 10;
tetha
=45*pi/180;
g =
9.81;
yo = 15;
t = 0:0.1:3;
x = Vo*cos(tetha)*t;
[tm
xm] = meshgrid(t,x);
ym = yo + Vo*sin(tetha)*tm-
g*tm.^2/2;
Vy = Vo*sin(tetha)- g*tm;
Vx =
ones(length(t))*Vo*cos(tetha);
[px,py]
= gradient(ym,.1,.1);
subplot(1,2,1);
mesh(tm,
xm, ym);
Title('Desplazamiento
del tiro parabolico');
xlabel('tiempo');
ylabel('x');
zlabel('y');
subplot(1,2,2);
quiver(Vx,Vy);
Title('Campo
vectorial de desplazamiento');
Ejemplo 9.
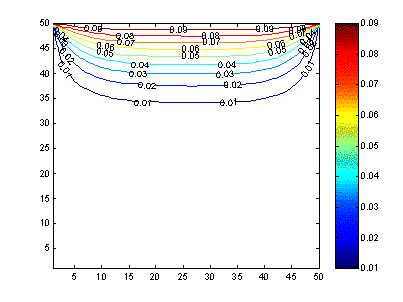
Determinar la distribución de potencial eléctrico en un
conductor cuadrado, utilizando diferencias finitas.
clear;
N =
50;
z =
zeros(N,N);
z(N,
:) = 0.1;
for iter = 1: 100
for n=2:N-1
for m=2:N-1
suma = 0;
suma = suma + z(n-1,m);
suma = suma + z(n+1,m);
suma = suma + z(n,m-1);
suma = suma + z(n,m+1);
z(n,m) = suma/4;
end;
end;
end;
[c,
h] = contour(z); clabel(c, h); colorbar;