Solución de ecuaciones lineales con MATLAB.

Consideremos un conjunto de n ecuaciones lineales con n variables, representado por:

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + ... + a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ + a₂₃x₃ + ... + a_2nx_n = b₂

a₃₁x₁ + a₃₂x₂ + a₃₃x₃ + ... + a_3nx_n = b₃

a_n1x₁ + a_n2x₂ + a_n3x₃ + ... + a_nnx_n = b_n

donde a_ij son los coeficientes, x_i son las variables a calcular y b_i los términos independietes.

El sistema anterior puede representarse de forma compacta por:

Ax=b

donde :

|a₁₁ a₁₂ a₁₃ ... a_1n |

|a₂₁ a₂₂ a₂₃ ... a_2n |

A = |a₃₁ a₃₂ a₃₃ ... a_3n |

| |

|a_n1 a_n2 a_n3 ... a_nn |

|b₁|

|b₂|

b= |b₃|

| |

|b_n|

|x₁|

|x₂|

x= |x₃|

| |

|x_n|

La solución de este sistema de ecuaciones esta dado por:

x = A\b

o de manera equivalente por

x = inv(A)*b

Ejemplo 1.

Para el circuito eléctrico mostrado en la figura calcular el valor de la corriente en cada una de las mallas.

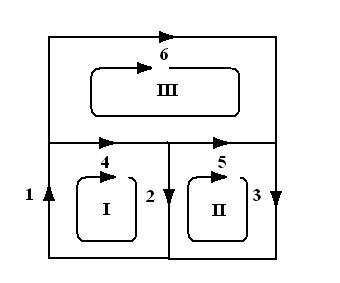
Los valores de resistencia y de fuentes de voltaje en cada elemento son

R = [1, 1, 1, 2, 3, 1] y E = [10, 0, 5, 0, 0, 0]

Solución:

A=[1,0,0; 1,-1,0; 0,-1,0; 1,0,-1; 0,1,-1; 0, 0, 1];

R=[1, 1, 1, 2, 3, 1]';

E=[10,0,5,0,0,0]';

n = 6;

Relem = zeros(n, n);

for i=1:6, Relem(i,i) = R(i), end;

Rmalla = A'*Relem*A

Emalla = A'*E

Imalla = Rmalla\Emalla

I = A*Imalla

Ejemplo 2.

Encontrar la línea recta que aproxima al conjunto de puntos dados por X =[1, 2, 3, 4, 5, 6, 7] y Y = [2.5, 4.5, 6, 10, 11.2, 12, 14.3].

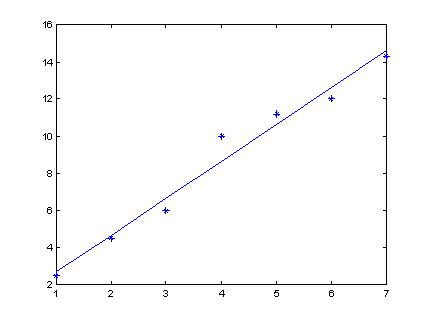
La ecuación de la línea recta esta dada por Y_i = mX_i + b, por lo tanto:

X₁ m + b = Y₁

X₂ m + b = Y₂

_...

X_N m + b = Y_N

En forma matricial podemos escribir:

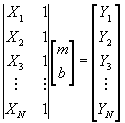
Lo cual es equivalente al sistema de ecuaciones Cp=y, donde :

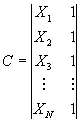
y

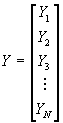
dado que tenemos un sistema de ecuaciones sobredeterminado, donde el número de ecuaciones es mayor que el número de incógnitas, no podemos calcular la solución exacta. Si multiplicamos ambos lados de la ecuación por C^T

C^TCp=C^Ty

Tenemos un sistema de ecuaciones que si podemos resolver. La solución la calculamos haciendo

p = [C^TC]^-1 C^Ty

La solución utilizando Matlab es:

% Valores iniciales

X =[1, 2, 3, 4, 5, 6, 7]';

Y = [2.5, 4.5, 6, 10, 11.2, 12, 14.3]';

% Grafica los puntos dados

plot(X, Y, '*')

% Calcula la matriz C

C = [X, ones(length(X),1)]

% Calculo de los parametros

p = inv(C'*C)*C'*Y

% Calcula los puntos de acuerdo con los parametros

Yc = C*p;

% Grafica la linea calculada

hold on;

plot(X, Yc)

Regresar.