Matemática Simbólica.
El toolbox de matemática
simbólica es una colección de herramientas para MATLAB que se usan para
manipular y resolver expresiones simbólicas.
Las expresiones simbólicas son
cadenas de caracteres, o arreglos de cadenas de caracteres que representan
números, funciones, operadores y variables.
Algunos ejemplos de
expresiones simbólicas son:
f1 =
'1/(2*x^2n)'
f2 =
'1/sqrt(2*x)'
f3 =
'cos(x^2) - sen(2*x)'
M =
sym('[a, b; c, d]')
f =
int('x^3/sqrt(1-x)', 'a', 'b')
Para efectuar la derivada de una función utilizamos
el comando diff.
diff('cos(x)')
como resultado tenemos
ans
= -sin(x)
Nota: Las expresiones simbólicas deberán ser escritas
sin espacios.
Para definir matrices hacemos:
M =
sym('[a, b; c, d]')
Y el cálculo
del determinante lo hacemos :
determ(M)
Después de la ejecución tenemos...
M =
[ a, b]
[ c, d]
ans =
a*d-b*c
Las expresiones simbólicas sin variables son llamadas
constantes simbólicas. Cuando se visualizan constantes simbólicas, a menudo son
difíciles de distinguir de los enteros.
f =
symop('(3*4-2)/5+1')
numeric(f)
Variables simbólicas.
El comando symvar, se utiliza para averiguar la variable
simbólica en la expresión.
symvar('a*x+y')
symvar('a*t+s/(u+3)')
symvar('sin(omega)')
symvar('3*i+4*j')
symvar('y+3*s', 't')
Muchos comandos dan la opción, si se desea, de
especificar las variables independientes:
diff('x^n')
diff('x^n', 'x')
diff('x^n', 'n')
ans = x^n*n/x
ans = x^n*n/x
ans = x^n*log(x)
Extracción de numeradores y denominadores.
El comando numden() se utiliza para determinar el
denominador y numerador de expresiones racionales.
clear;
a =
sym('a');
b =
sym('b');
x = sym('x');
f =
a*x^2/(b-x)
[n m] = numden(f)
Otro ejemplo es:
clear;
x =
sym('x');
f =
3/2*x^2+2/3*x-3/5
[n m] = numden(f)
Operaciones algebraicas estándar.
Las cuatro operaciones de suma, resta, multiplicación y división
se realizan de manera similar, como ejemplo consideremos:
clear;
x =
sym('x');
f =
2*x^2+3*x-5
g =
x^2-x+7
display('suma'); f+g
display('resta');f-g
display('multiplicacion');f*g
display('division'); f/g
La respuesta que produce es:
suma
3*x^2+2*x+2
resta
x^2+4*x-12
multiplicacion
(2*x^2+3*x-5)*(x^2-x+7)
division
(2*x^2+3*x-5)/(x^2-x+7)
Sustitución de variables.
Para remplazar el valor de una variable por otra variable
o número utilizamos el comando subs()
a =
sym('a');
b =
sym('b');
c =
sym('c');
x =
sym('x');
f =
a*x^2+b*x+ c
subs(f,
's', 'x')
subs(f,
'A', 'a')
Ejemplo 1.
Resolver x –
cos(x) =0 utilizando matemática simbólica y el método de Newton.
clear
;
p=
2.5;
x =
sym('x');
fx = x- cos(x);
h =
fx/diff(fx);
while abs(numeric(subs(fx, num2str (p), 'x'))) > 0.001
p = p - numeric(subs(h, num2str (p), 'x'))
end;
z =
p;
Ejemplo 2.
Calcular los ceros del conjunto de funciones
f1(x,y) = x2 - 2x – y + 0.5
f2(x,y) = x2 + 4y2 - 4
Utilice el método de Newton Raphson y considere como
punto inicial p=[1,1]
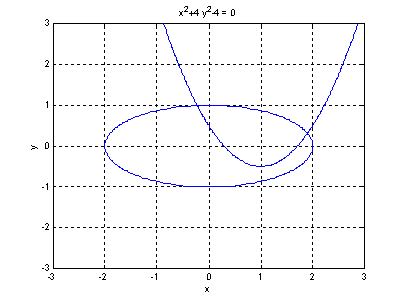
La implementación en MATLAB queda:
p =
[1; 1]
x =
sym('x');
y = sym('y');
f = [x^2-2*x-y+0.5;
x^2+4*y^2-4]
ezplot(f(1),[-3,3]);
hold
on;
ezplot(f(2),[-3,3]);
grid
on;
J = [diff(f(1),x),
diff(f(1), y); diff(f(2),x), diff(f(2), y)]
for k=1:100
k
Ji = subs(subs(J, x, num2str(p(1))), y,
num2str(p(2)))
fi = subs(subs(f, x, num2str(p(1))), y,
num2str(p(2)))
p = p - numeric(inv(Ji)*fi)
pause
if(max(abs(numeric(fi)))
< 0.001) break; end;
end;
Integración.
La función de integración int(f), donde f es una
función simbólica, intenta obtener otra expresión simbólica F tal que diff(F) =
f.
Cuando MATLAB no puede encontrar la antiderivada,
devuelve el comando sin evaluar.
Por ejemplo
int('log(x)/exp(x^2)')
Regresa.
Warning: Explicit integral could not be found.
> In C:\MATLABR11\toolbox\symbolic\@sym\int.m at
line 58
In
C:\MATLABR11\toolbox\symbolic\@char\int.m at line 9
In
C:\MATLABR11\work\eje133.m at line 1
ans =
int(log(x)/exp(x^2),x)
Cuando se realiza la derivada podemos decir respecto a
que variable deseamos hacer la integración, en el caso de no expresarlo, por
default se hará con respecto a x.
x =
sym('x');
s =
sym('s');
f =
sin(s + 2*x)
int(f)
int(f,s)
Regresara.
f =
sin(s+2*x)
ans =
-1/2*cos(s+2*x)
ans
=
-cos(s+2*x)
Ejemplo 3.
Bart ha salido de excursión con su clase a la cima del
edificio Skiley en el centro de Springfield. Coge un tomate maduro de la bolsa
de comida, se apoya en el borde del tejado, y lo lanza hacia arriba. El tomate
sale recto, con una velocidad inicial de v0 = 64 pies por
segundo. El tejado esta a y0 = 96 pies por encima del suelo. ¿Dónde
está el tomate t segundos más tarde?. ¿Cuándo alcaza su máxima altura?. ¿Qué altura
máxima sobre el suelo alcanza el tomate?. ¿Cuándo golpea el tomate el suelo?.
Suponer que no hay resistencia del aire y que la aceleración debida a la gravedad
es una constante g = -32 pies por segundo por segundo en Springfield.
clear;
g =
sym('g')
t =
sym('t')
g = -32 %
aceleracion de la gravedad.
v = int(g, t) %
calcula la velocida como función del tiempo
v = symadd(v, 64) % en t=0
la velocidad en 64
y = int(v, t) %integra
la velocidad respecto a t para calcular el desplazamiento
fprintf('El valor de desplazamiento en funcion de t es \n');
y = symadd(y, 96) % en t=0
la altura es 96 pies
fprintf('La pelota alcnza la altura máxima cuando\n');
t_max = solve(v) % calcula
v(t) = 0
fprintf('La altura máxima es \n');
y_max = subs(y, t_max)
fprintf('El tiempo para que el tomate golpe el suelo es\n')
t_fin = solve(y)
La solución que entrega MATLAB es:
g = -32
v = -32*t
v = -32*t+64
y = -16*t^2+64*t
El
valor de desplazamiento en funcion de t es
y = -16*t^2+64*t+96
La
pelota alcnza la altura máxima cuando
t_max
= 2
La
altura máxima es
y_max
= 160
El
tiempo para que el tomate golpe el suelo es
t_fin
= [ 2+10^(1/2)]
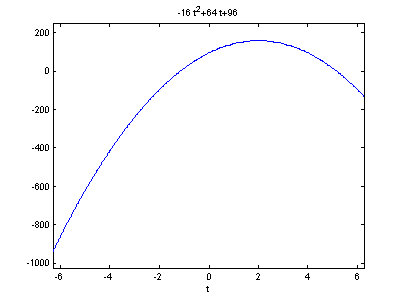
Para
tener una idea más clara de lo que le paso al tomate, vamos a dibujar el
resultado del lanzamiento del tomate. Para ello utilizamos el comando ezplot(y)
Simplificación
de expresiones.
Las expresiones simbólicas pueden ser presentadas de
muchas formas equivalentes. En situaciones diferentes algunas formas pueden ser
preferibles a otras. MATLAB usa un número de comandos para simplificar la forma
de las expresiones simbólicas.
» f = sym('(x^2-1)*(x-2)*(x-3)')
f =
(x^2-1)*(x-2)*(x-3)
»
collect(f)
ans =
x^4-5*x^3+5*x^2+5*x-6
» horner(ans)
ans =
-6+(5+(5+(-5+x)*x)*x)*x
» factor(ans)
ans =
(x-1)*(x-2)*(x-3)*(x+1)
» expand(f)
ans =
x^4-5*x^3+5*x^2+5*x-6
simplify es una herramienta potente, de propósito general,
que intenta simplificar una expresión mediante la aplicación de muchas clases
diferentes de identidades algebraicas involucrando sumas, integrales y
potencias fraccionales, así como trigonometría, fórmulas exponenciales,
funciones logarítmicas, etc.
Algunos de ejemplos de uso de este comando son
x =
sym('x')
y = sym('y')
f = log(2*x/y)
simplify(f)
La respuesta a estos comandos es:
f =
log(2*x/y)
ans =
log(2)+log(x/y)
Otro ejemplo es
x =
sym('x')
g = sin(x)^2+3*x+cos(x)^2-5
simplify(g)
La
respuesta en este caso es:
g =
sin(x)^2+3*x+cos(x)^2-5
ans =
-4+3*x
Otro es
x =
sym('x')
h =
(1/x^3+6/x^2+12/x+8)^(1/3)
simplify(h)
Solución de ecuaciones algebraicas simples.
Para calcular la solución de una ecuación algebraica
simple se utiliza el comando solve()
solve('a*x^2+b*x+c')
solve('x=cos(x)')
solve('exp(x)=tan(x)')
La respuesta a estos comandos es:
ans =
[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))]
[ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]
ans =
.73908513321516064165531208767387
ans =
1.3063269404230792361743566584407
Solución de ecuaciones diferenciales.
En la solución de ecuaciones diferenciales utilizamos el
comando dsolve así por ejemplo
![]()
se soluciona haciendo
dsolve('Dy=1+y^2')
ans =
tan(t+C1)
Vamos
a probar una ecuación diferencial de segundo orden.
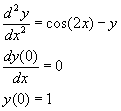
y = dsolve('D2y=cos(2*x)-y', 'Dy(0)=0',
'y(0)=1')
También el comando dsolve puede resolver sistemas de
dos ecuaciones diferenciales simultaneas.
[f,
g] = dsolve('Df=3*f+4*g', 'Dg=-4*f+3*g')