Análisis de
componentes principales
El Análisis de
Componentes Principales (ACP o PCA en inglés) es una técnica estadística de
síntesis de la información, o reducción de la dimensión (número de variables).
Es decir, ante un banco de datos con muchas variables, el objetivo será
reducirlas a un menor número perdiendo la menor cantidad de información
posible. Los nuevos componentes principales o factores serán una combinación
lineal de las variables originales, y además serán independientes entre sí. Un
aspecto clave en PCA es la interpretación de los factores, ya que ésta no viene
dada a priori, sino que será deducida tras observar la relación de los factores
con las variables iniciales (habrá, pues, que estudiar tanto el signo como la
magnitud de las correlaciones). Esto no siempre es fácil, y será de vital
importancia el conocimiento que el experto tenga sobre la materia de
investigación.
Objetivos
• Entender por
qué es importante reducir la dimensión en un problema estadístico.
• Saber aplicar
el análisis de componentes principales, con ayuda de Minitab.
• Conocer
pautas para elegir el modelo más adecuado para nuestro problema.
• Interpretar
los factores del modelo obtenido.
Motivación
Consideremos
un conjunto de datos en dos dimensiones dado por
|
|
1 |
1 |
|
|
2 |
2 |
|
X= |
3 |
3 |
|
|
4 |
4 |
|
|
5 |
5 |
Para
hacer el cálculo de la matriz de covarianza muestral, hacemos S = XTX/N (estimador sesgado de la
Covarianza ) donde N es el total de muestras. La matriz de covarianza resulta
ser
|
S = |
11 |
11 |
|
|
11 |
11 |
Para
la matriz de covarianza podemos notar que su determinante es cero (11*11 – 11*11
=0) lo que significa su inversa no existe. ¿A que se debe dicha condición?.
Veamos como lucen en una gráfica dichos puntos.
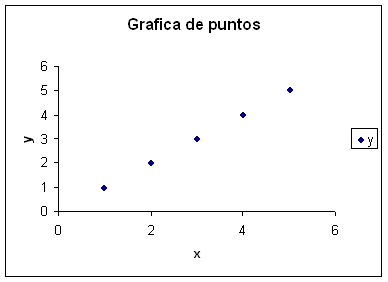
En
realidad podemos notar que solo existe variación en una dirección, dicha
dirección esta a 45 grados (q = atan (1/1) … q = atan (5/5) ) de acuerdo con los valores.
Ahora porque no podemos sacar la inversa. Sacar la inversa de una matriz es
equivalente a solucionar un sistema de ecuaciones así para nuestra matriz de
covarianza un sistema equivalente es
11 x + 11 y = b1
11 x + 11 y = b2
Note
que ambas ecuaciones son la misma y que por lo tanto no tengo un sistema
completo de ecuaciones. Ambas ecuaciones son paralelas y la solución gráfica es
el punto donde ambas ecuaciones se interceptan. Si embargo volviendo al
problema de la varianza, es necesario calcular la covarianza dado que vemos
variación en una dirección.
Descomposición en
valores singulares.
Consideremos
que nuestros datos pueden ser modelados por una distribución gausiana, como la
siguiente
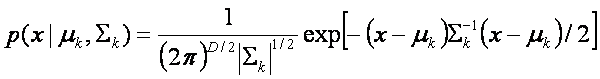
El término dentro de la exponencial
asumiendo que la media es cero, lo podemos usarlo para explicar el
procedimiento
xTS-1x
Si
aplicamos una matriz de rotación R a
los ejes coordenados y recordando que la transpuesta de una matriz de rotación
es equivalente a la inversa de esta, podemos escribir esta expresión como
xT(RTR)TS-1(RTR )x
(Rx)T(RS-1R)
Rx
yT(RS-1R)
y
Lo
interesante de esta transformación es tomar una matriz de rotación que haga a
la matriz de covarianza un matriz diagonal. Eso es precisamente lo que hace la
descomposición en valores singulares. Así dada un matriz la descomposición en
valores singulares la escribimos como A = UDV, donde U y V son matrices de
rotación de acuerdo a nuestro desarrollo anterior y D es una matriz diagonal a
la cual se le llama la matriz de eigenvalores D = diag[l1, l2, …, ln].
li es el i-esimo
eigenvalor o factor.
Para
los datos que hemos estado manejando tenemos que la descomposición en valores
singulares de a es A = UDV
|
A= |
|
-0.7071 |
-0.7071 |
|
22 |
0 |
|
-0.7071 |
-0.7071 |
|
|
|
-0.7071 |
0.7071 |
|
0 |
0 |
|
-0.7071 |
0.7071 |
Note que la matriz D es una diagonal y para
nuestro nuevo sistema de referencia podemos ver que el eigenvalor principal es
igual a 22 y en el segundo eigenvalor es cero. En este caso las matrices U y V
son iguales y cada columna de estas matrices es un eigenvector. Los
eigenvectores dan la dirección de las componentes principales. Note en este
caso que la dirección del eigenvector principal (columna 1) es 270 grados y del
segundo eigenvalor es 135 grados.
v1 = -0.7071 i - 0.7071j q = tg-1(-0.7071/-0.7071) = 270°
v2 = -0.7071 i + 0.7071j q = tg-1(0.7071/-0.7071) = 135°
Uno de los objetivos de hacer el análisis en
componentes principales (PCA), es resolver este tipo de problemas, reduciendo
la dimensionalidad de nuestros datos. Una vez que se aplica las matrices de
rotación a los puntos de entrada y se selecciona el número de factores de
nuestro análisis. En este caso el número de factores será uno dado que uno de
los eigenvalores o factores es cero
PCA
en MINITAB
Para llevar a cabo este procedimiento en
MINITAB hacemos:
Ir al menú Stat > Multivariate >
Principal Components…
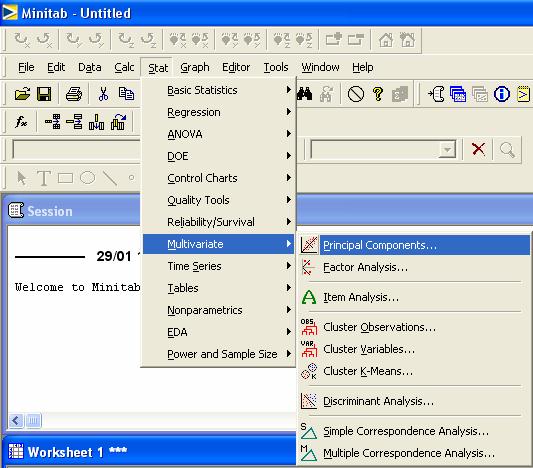
Al seleccionar la opción aparecerá
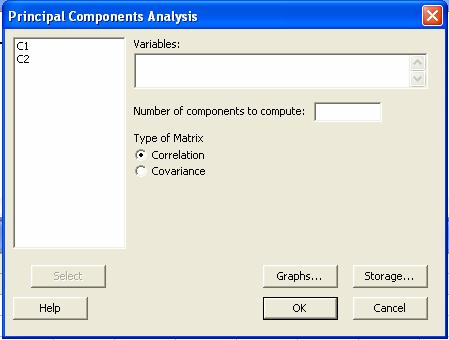
En la opción Storage damos los lugares donde guardaremos los valores
transformados
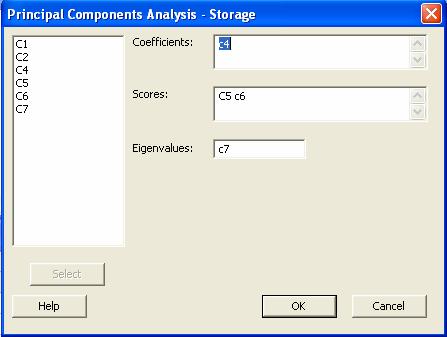
Selección de
los factores
La elección de
los factores se realiza de tal forma que el primero recoja la mayor proporción
posible de la variabilidad original; el segundo factor debe recoger la máxima
variabilidad posible no recogida por el primero, y así sucesivamente. Del total
de factores se elegirán aquéllos que recojan el porcentaje de variabilidad que
se considere suficiente. A éstos se les denominará componentes principales.
Ejemplo 1
Considere
los datos
|
|
1 |
1 |
|
|
2 |
2 |
|
X= |
3 |
3 |
|
|
4 |
4 |
|
|
5 |
5 |
Calcular
las eigenvalores, eigenvectores y datos transformados utilizando MINITAB
Principal
Component Analysis: C1, C2
Eigenanalysis of the Covariance Matrix
Eigenvalue 5.0000
0.0000
Proportion 1.000
0.000
Cumulative 1.000
1.000
Variable PC1
PC2
C1 0.707
0.707
C2 0.707
-0.707
Los
datos transformados son
1.41421 0
2.82843 0
4.24264 0
5.65685 0
7.07107 0
La
grafica correspondiente a los eigenvalores o valores principales es
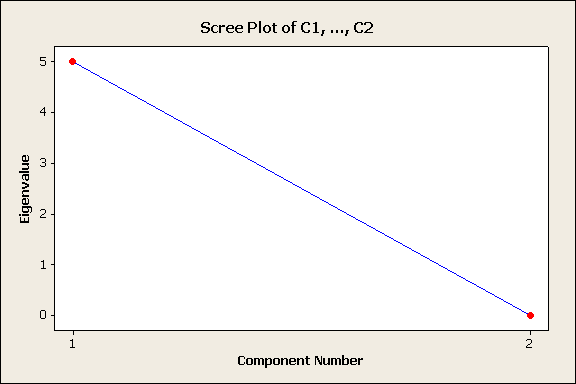
Ejemplo 2
Considere
los datos de la imagen y haga el análisis en componentes principales
Results
for: Imagen.MTW
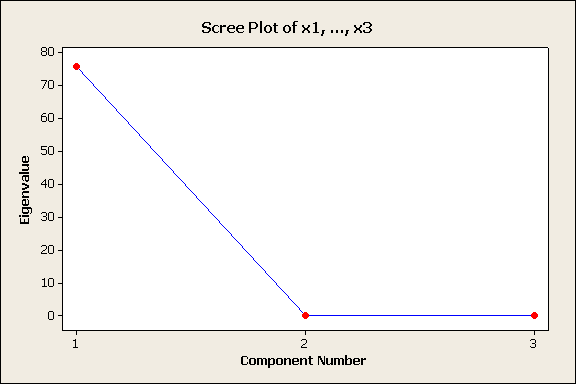
Principal
Component Analysis: x1, x2, x3
Eigenanalysis of the Covariance Matrix
Eigenvalue 75.883 -0.000
-0.000
Proportion 1.000
-0.000 -0.000
Cumulative 1.000
1.000 1.000
Variable PC1
PC2 PC3
x1 0.577
0.789 -0.211
x2 0.577
-0.211 0.789
x3 0.577
-0.577 -0.577
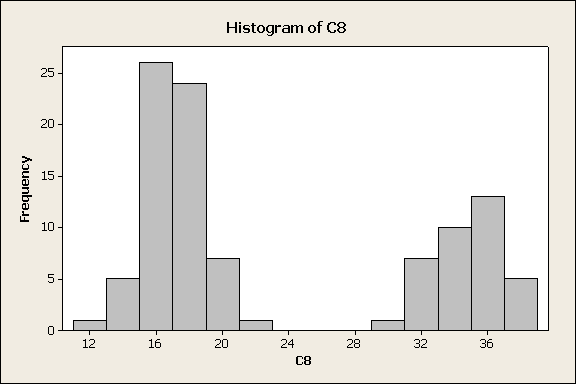
b)
dibuje el histograma del componente principal.
c)
Cual es la función discriminante del componente principal
Discriminant
Analysis: tono versus C8
Linear Method for Response: tono
Predictors: C8
Group 10 20
Count 64 36
Summary of classification
True Group
Put into Group 10 20
10 64 0
20 0 36
Total N 64 36
N correct 64 36
Proportion 1.000 1.000
N = 100 N Correct =
100 Proportion Correct = 1.000
Squared Distance Between Groups
10 20
10 0.0000 94.5161
20 94.5161 0.0000
Linear Discriminant Function for Groups
10 20
Constant -44.60
-183.67
C8 5.20 10.55
La función de la frontera queda dada por
139.07 -5.35y1 = 0
y1 = 25.994
Ejemplo 3
La
resistencia a la tracción de una unión de alambre es una característica
importante. El archivo resistencia.mtw, brinda información sobre la resistencia
a la tracción y, la altura del molde x1, la altura del perno x2, la altura del lazo x3, longitud del alambre x4, ancho de la unión sobre
el molde x5 y ancho del
molde sobre el perno x6.
a)
hacer el análisis en componentes principales y decir cuales son las variables
con los dos componentes principales
b)
hacer la transformación de los datos al nuevo sistema y graficar.
c)
hacer el análisis de varianza para el conjunto transformado considerando
solamente dos factores.