Análisis de Varianza.
1.
Mínimos cuadrados.
Suponga
que tenemos n puntos de datos experimentales en la forma acostumbrada [xi, yi]
y que se estima la línea de regresión utilizando mínimos cuadrados. Definimos
la suma de los errores al cuadrado SSE
como:
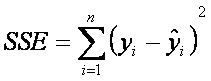
donde los
valores sobre la recta calculada son
![]()
y a y b los parámetros de la ecuación de la recta, la cual podemos
calcular resolviendo el sistema de ecuaciones

En forma
compacta podemos escribir como Mp=y; y la solución esta dada por p = [MTM]-1MTy con p=[b,a]T
Ejemplo
1.
Calcular
la recta de mínimos cuadrados dada por el conjunto de datos:
x
= [ 1 2 3 4
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20]
y
= [ 2.6888
-0.4724 3.7286 5.6471
1.1164 4.3160 5.2080
-0.3875 0.0181 4.1423
2.3002 4.5800 4.9312
4.8238 6.0805 4.9372
6.0817 1.3951 3.8604
3.6866]
La
gráfica para estos datos la podemos ver en la Figura
1.
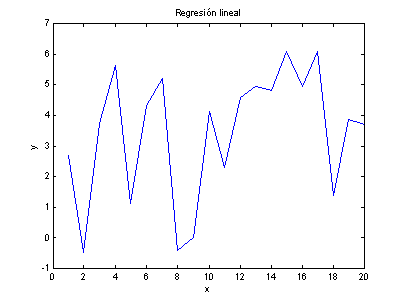
Figura 1
La solución para este
utilizado MATLAB es:
clear;
x = [ 1 2 3
4 5 6
7 8 9 10 11 12 13 14 15 16 17 18 19 20]';
y = [ 2.6888 -0.4724
3.7286 5.6471 1.1164
4.3160 5.2080 -0.3875
0.0181 4.1423 2.3002
4.5800 4.9312 4.8238
6.0805 4.9372 6.0817
1.3951 3.8604 3.6866]';
n = length(x);
plot(x,y);
title('Regresión lineal');
xlabel('x');
ylabel('y');
M
= [x, ones(n, 1)];
p
= inv(M'*M)*M'*y;
b
= p(1)
a
= p(2)
Una vez ejecutado el código
tenemos b = 0.1180 y a = 2.1953, con una ecuación y = 0.1180
x +
2.1953.
Es importante notar, que el
hecho de ajustar una línea recta a un conjunto de datos significa que verdaderamente
exista una dependencia lineal entre ellos. Así pues, para los datos en la Figura
1, queremos averiguar hasta donde la variable y
depende de x.
2.
Varianza.
La
cantidad s2 se llama
varianza de muestra y se calcula con la siguiente expresión
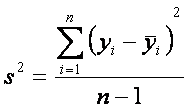
Debe
quedar claro que la varianza es una medida de la variabilidad de los datos
respecto a una referencia, en este caso la media ![]() . La cantidad n-1 se denomina grados de libertad.
. La cantidad n-1 se denomina grados de libertad.
Para
el caso de mínimos cuadrados ecuación (1), definimos una varianza con (n-2) grados de libertad, dada por:
Ecuación 1
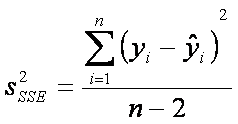
la cual
mide la brecha entre los puntos dados y la recta calculada ![]() .
.
También
podemos definir una varianza entre la recta de mínimos cuadrados respecto a la
media de los datos, con un grado de libertad como:
Ecuación 2
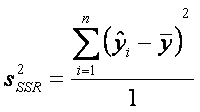
con
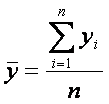
Note
que la Ecuación
2, mide que tanto difiere la línea de mínimos cuadrados
respecto de la media.
Ejemplo
2.
Calcular
las varianzas sSSR y sSSE
para los datos del ejemplo 1.
clear;
x = [ 1 2 3
4 5 6
7 8 9 10 11 12 13 14 15 16 17 18 19 20]';
y = [ 2.6888 -0.4724
3.7286 5.6471 1.1164
4.3160 5.2080 -0.3875
0.0181 4.1423 2.3002
4.5800 4.9312 4.8238
6.0805 4.9372
6.0817 1.3951 3.8604
3.6866]';
n = length(x);
plot(x,y);
hold on;
title('Regresión
lineal');
xlabel('x');
ylabel('y');
M = [x, ones(n, 1)];
p = inv(M'*M)*M'*y;
m = p(1)
b = p(2)
yp = mean(y)
v1 = 1;
v2 = n-2;
plot(x, M*p, 'r');
plot(x, ones(n,1)*yp, 'g');
SSR = (yp -m*x - b)'*(yp -m*x
- b)
SSE
= (y -m*x - b)'*(y -m*x -
b);
s2_SSE = SSE/v2
s2_SSR = SSR/v1
Los
resultados son:
s2_SSE
= 4.1701
s2_SSR
= 9.2571
Podemos
ver la recta de mínimos cuadrados y la media en la Figura 2.
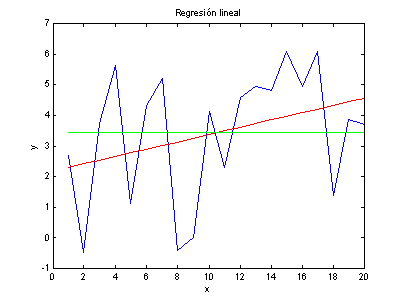
Figura 2
En
este momento podríamos concluir dado las varianzas que hay menor diferencia
entre los datos y la recta de mínimos cuadrados, que entre la media de los
datos y esta misma recta.
3.
La distribución F.
La
distribución F encuentra enorme aplicación en la comparación de
varianzas muéstrales. La estadística F se define como la razón de cambio
de dos variables aleatorias ji cuadrada independientes, dividida cada una entre su número de grados
de libertad. De aquí, que podamos escribir:
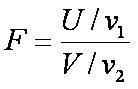
Basados
en esto podemos mostrar que la Ecuación
1 y Ecuación
2 son distribuciones ji
cuadrada y que el cociente tiene por lo
tanto una distribución F. (ver [Walpole et all]) dada por:
Ecuación 3
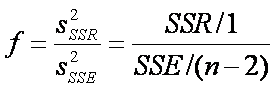
La
distribución de la variable aleatoria F esta dada por:
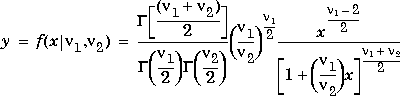
La
curva de distribución F depende no sólo de los dos parámetros v1
y v2 sino también del orden en que se establecen. En la Figura 3, tenemos la gráfica de la distribución F(x, 6, 24),
la cual fue calculada utilizando MATLAB.
clear;
f = 0:0.1:10;
plot(f, fpdf(f, 6, 24));
title('Distribución
F con 6 y 24 grados de libertad');
xlabel('f');
ylabel('h(f)');
[m, v] =fstat(6,24)
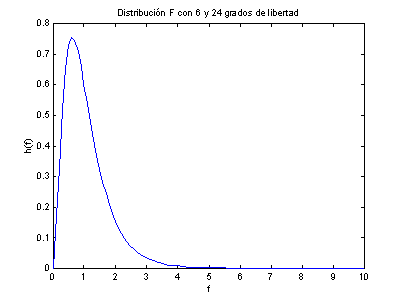
Figura 3
La media y la varianza se
calcula utilizando [m, v] =fstat(6,24).
Si
integramos la función F de 1 a infinito, nos daremos cuenta, que el área
bajo la curva es 1. En algunos problemas será interesante determinar el valor
de fa que parte a la curva en porcentaje (1-a) (a es llamado el
nivel de significancia). Para esto tenemos que
calcular el valor de fa que satisfaga la ecuación:
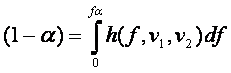
Este
dato puede ser calculado utilizando la función de MATLAB utilizando la función
finv((1-alfa), v1, v2)
Ejemplo
3.
Determinar
el valor crítico para una distribución F con 6 y 24 grados de libertad en un
nivel de significacia de 0.05. Graficar la
distribución el valor crítico.
clear;
f
= 0:0.1:10;
plot(f, fpdf(f, 6, 24));
title('Distribución
F con 6 y 24 grados de libertad');
xlabel('f');
ylabel('h(f)');
[m, v] =fstat(6,24)
fa = finv(0.95, 6, 24)
hold on;
y = 0:0.1:0.8;
plot(ones(length(y),1)*fa,
y, 'r');
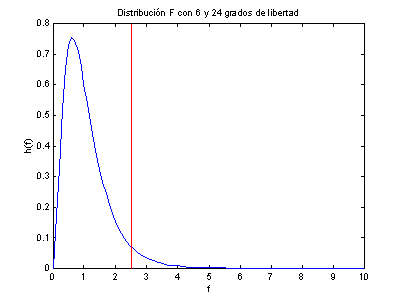
Figura 4
Podemos
ver en la Figura
4, que el 95% de los datos se concentran a la izquierda
de la línea roja y solo un 5% a la derecha.
4.
Prueba de Hipótesis.
Una
hipótesis estadística es una aseveración o conjetura con respecto a una o más
poblaciones.
La
estructura de la prueba de hipótesis se formulará con el uso del término de
hipótesis nula, el cual se refiere a cualquier hipótesis que deseamos probar y
se denota con H0. El rechazo de H0 conduce a la aceptación de la hipótesis
alternativa.
Errores.
· El rechazo de la hipótesis nula cuando es verdadera se
llama error tipo I.
· La aceptación de hipótesis nula cuando es falsa se
llama error tipo II.
Al
probar cualquier hipótesis estadística, hay cuatro situaciones
|
|
H0 es verdadero
|
H0 es falsa
|
Aceptar H0
|
Decisión correcta |
Error tipo II |
Rechazar H0
|
Error Tipo I |
Decisión correcta |
La
probabilidad de cometer un error tipo I, también llamada nivel de significancia, se denota con la letra griega a.
5.
Procedimiento del análisis de varianza.
Con
frecuencia el problema de analizar la calidad de la línea de regresión estimada
se maneja mediante un enfoque de análisis de varianza: un procedimiento por el
que la variación de la total en la variable dependiente se subdivide en
componentes significativos que se observan y tratan en forma sistemática.
Suponga
que tenemos n puntos de datos experimentales en la forma acostumbrada (xi, yi)
y que se estima la recta de regresión
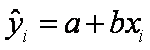
Una
formulación alternativa y quizá más informativa es
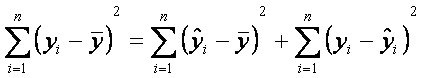
Por
lo cual logramos una partición de la suma total corregida de cuadrados de y
en dos componentes que deben reflejar un significado particular para el
experimentador. Indicaremos esta partición de manera simbólica como
SST = SSR + SSE
donde:
SSR
= 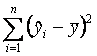 es la suma de cuadrados de regresión y refleja las
variaciones sobre la media.
es la suma de cuadrados de regresión y refleja las
variaciones sobre la media.
SSE
= 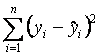 es la suma de
cuadrados del error y refleja las variaciones sobre la recta de regresión
es la suma de
cuadrados del error y refleja las variaciones sobre la recta de regresión
Supongamos
que nos interesa probar la hipótesis
H0 : b es igual a cero
H1 : b es diferente de cero
Lo que significa que los valores de y no
dependen de x y que probablemente fueron generados de manera aleatoria
independientemente de x.
Para probar la hipótesis anterior calculamos
Ecuación 4
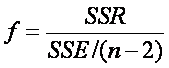
donde f
es una distribución f y rechazamos H0 al nivel de significancia a cuando f > fa(1, n-2)
Los
cálculos por lo general se resumen por medio de una tabla de análisis de
varianza como la siguiente.
Análisis de variancia para probar
b =0
|
||||
|
Fuente de variación |
Suma de cuadrados |
Grados de libertad |
Cuadrado medio |
f calculada |
|
Regresión |
SSR |
1 |
SSR |
SSR/ s2 |
|
Error |
SSE |
n-2 |
s2=SSE/(n-2) |
|
|
Total |
SST |
n-1 |
|
|
|
rechazamos b=0,
al nivel de significancia a cuando f > fa(1,
n-2) |
||||
La media de los datos es una línea recta con
pendiente cero y la línea de mínimos cuadrados es una línea recta con pendiente
diferente de cero b!=0. En
esta prueba de hipótesis más que probar si no hay dependencia lineal, esta
probando que la varianza de los datos calculados respecto a la media es similar
a la varianza de los datos calculados
respecto a la línea de mínimos cuadrados.
Ejemplo
4.
Determinar,
para los datos del ejemplo 1, si existe dependencia lineal de y respecto
de x.
La
implementación en MATLAB es:
clear;
x = [ 1 2 3
4 5 6
7 8 9 10 11 12 13 14 15 16 17 18 19 20]';
y = [ 2.6888 -0.4724
3.7286 5.6471 1.1164
4.3160 5.2080
-0.3875 0.0181 4.1423
2.3002 4.5800 4.9312
4.8238 6.0805 4.9372
6.0817 1.3951 3.8604
3.6866]';
n = length(x);
plot(x,y);
title('Regresión lineal');
xlabel('x');
ylabel('y');
d
= [x, ones(n, 1)];
p
= inv(d'*d)*d'*y;
m = p(1);
b = p(2);
yp = mean(y);
v1 = 1;
v2 = n-2;
SSR = (yp -m*x - b)'*(yp -m*x
- b)
SSE
= (y -m*x - b)'*(y -m*x -
b);
SST = SSR + SSE;
s2 = SSE/v2;
F = SSR/s2;
alfa = 0.05;
Fc = finv(1-alfa, v1, v2);
fprintf('---------------------------------------------------------------------\n');
fprintf('Curva ajustada\n');
fprintf('y = %13.3f
*x + %13.3f\n', m, b);
fprintf('---------------------------------------------------------------------\n');
fprintf('Analisis
de Varianza\n');
fprintf('---------------------------------------------------------------------\n');
fprintf('Fuente de Suma Grados de Cuadrado F calc\n');
fprintf('Variacion cuadrados Libertad medio \n');
fprintf('---------------------------------------------------------------------\n');
fprintf('Regresion %13.2f
%13.f %13.2f %13.2f\n',
SSR, v1, SSR/v1, F);
fprintf('Error
%13.2f %13.f %13.2f \n', SSE, v2, s2);
fprintf('Total
%13.2f %13.f \n', SST, v1+v2);
fprintf('---------------------------------------------------------------------\n');
fprintf('Con (1-alfa) = %5.3f tenemos %13.2f > %13.2f\n',
1-alfa, F, Fc);
Los
resultados de la ejecución son:
---------------------------------------------------------------------
Curva ajustada
y =
0.118 *x + 2.195
---------------------------------------------------------------------
Analisis de Varianza
---------------------------------------------------------------------
Fuente de
Suma Grados de Cuadrado F calc
Variacion cuadrados Libertad medio
---------------------------------------------------------------------
Regresion 9.26 1 9.26 2.22
Error
75.06 18 4.17
Total
84.32 19
---------------------------------------------------------------------
Con (1-alfa) = 0.950 tenemos 2.22 > 4.41
Dado
los valores la hipótesis nula debe ser aceptada ya que la f calculada es
menor que la f para el nivel de significancia. Esto
significa que para nuestro experimento, no se da la dependencia lineal entre la
variable x y y.
Para
entender mejor esto hagamos la gráfica correspondiente para una distribución h(f, 1, 18).
f = 0:0.05:8;
v1 = 1;
v2 = 18;
alfa = 0.05;
plot(f, fpdf(f, v1, v2));
title('Distribución F');
xlabel('f');
ylabel('h(f)');
[m, v] =fstat(v1,v2)
fa = finv(1-alfa, v1, v2)
hold on;
y = 0:0.1:0.8;
plot(ones(length(y),1)*fa, y, 'r');
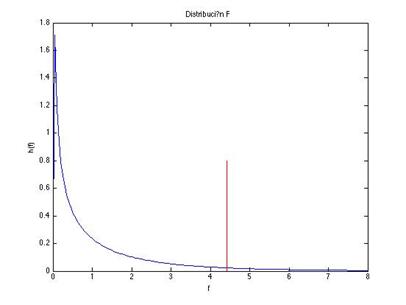
En
la figura podemos ver que a la izquierda de la línea roja las varianzas motivo
de nuestro análisis son iguales y a la derecha son diferentes. Nuestro valor
calculado de f es 2.22 lo cual significa que la varianza S_SSR
es igual a la varianza S_SSE. Esto
significa que la media describe de manera similar a la recta de mínimos
cuadrados las variaciones en los datos y por lo tanto se concluye que no hay
dependencia lineal.
6. Uso de MINITAB para el análisis de
Varianza
Podemos
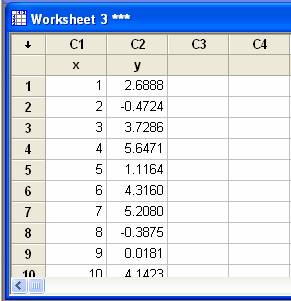
llevar a cabo este procedimiento utilizando MINITAB, para ello tenemos que
ingresar los datos en la hoja de trabajo de la siguiente manera o abriendo el
archivo ejemplo4.mtw.
Ir
a la opcion Stat >
Regresión > Regression …
Ahí
aparecerá la opción
Al
dar OK la solución que da MINITAB, es la siguiente
Regression
Analysis: y versus x
The regression equation is
y = 2.20 + 0.118 x
Predictor Coef SE Coef T
P
Constant 2.1953 0.9486
2.31 0.033
x 0.11799 0.07919
1.49 0.154
S = 2.04208 R-Sq = 11.0% R-Sq(adj) = 6.0%
Analysis of Variance
Source DF SS
MS F P
Regression 1
9.257 9.257 2.22
0.154
Residual Error 18
75.062 4.170
Total 19
84.319
Podemos ver que el
resultado de la f calculada es de 2.22 y será necesario calcular el valor del
estadístico f para completar la prueba de hipótesis. Sin embargo, tenemos
un dato adicional el valor P. Este valor indica que la hipótesis Ho (b=0) es valida con nivel de significancía
de 15.4 % muy superior al valor que deseamos del 5%. Por lo tanto la hipótesis
se acepta y no existe evidencia de dependencia lineal en el nivel de significancia.
Ejemplo
5.
Uno de los problemas más
desafiantes que enfrenta el campo de control de la contaminación del agua lo
presenta la industria del curtido de pieles. Los desechos de las curtidurías
son químicamente complejos. Se caracterizan por los altos valores de demanda
bioquímica de oxígeno, sólidos volátiles y otras medidas de contaminación.
Considérese los datos experimentales de la siguiente tabla que se obtuvieron
con 33 muestras de desechos químicamente tratados.
|
Reducción de Sólidos |
Demanda química de oxígeno |
|
x(%) |
y(%) |
|
3 |
5 |
|
7 |
11 |
|
11 |
21 |
|
15 |
16 |
|
18 |
16 |
|
27 |
28 |
|
29 |
27 |
|
30 |
25 |
|
30 |
35 |
|
31 |
30 |
|
31 |
40 |
|
32 |
32 |
|
33 |
34 |
|
33 |
32 |
|
34 |
34 |
|
36 |
37 |
|
36 |
38 |
|
36 |
34 |
|
37 |
36 |
|
38 |
38 |
|
39 |
37 |
|
39 |
36 |
|
39 |
45 |
|
40 |
39 |
|
41 |
41 |
|
42 |
40 |
|
42 |
44 |
|
43 |
37 |
|
44 |
44 |
|
45 |
46 |
|
46 |
46 |
|
47 |
49 |
|
50 |
51 |
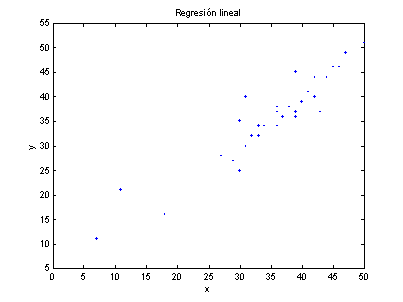
Figura 5
Hacer el análisis para
determinar si existe dependencia lineal entre los datos.
---------------------------------------------------------------------
Curva
ajustada
y
= 0.904 *x + 3.830
---------------------------------------------------------------------
Análisis
de Varianza
---------------------------------------------------------------------
Fuente
de Suma Grados de Cuadrado F calc
Variación cuadrados Libertad medio
---------------------------------------------------------------------
Regresión 3390.55 1 3390.55 325.08
Error 323.33 31 10.43
Total 3713.88 32
---------------------------------------------------------------------
Con
(1-alfa) = 0.950 tenemos 325.08
> 4.16
De acuerdo al análisis de
varianza, se rechaza la hipótesis nula, es decir, existe suficiente evidencia
de la dependencia lineal.
La corrida en MINITAB con
los datos contaminacion.mtw fue
Results
for: contaminacion.MTW
Regression
Analysis: y versus x
The regression equation is
y = 3.83 + 0.904 x
Predictor Coef SE Coef T
P
Constant 3.830 1.768
2.17 0.038
x 0.90364 0.05012
18.03 0.000
S = 3.22954 R-Sq = 91.3% R-Sq(adj) = 91.0%
Analysis of Variance
Source DF SS
MS F P
Regression 1 3390.6
3390.6 325.08 0.000
Residual Error 31 323.3
10.4
Total 32 3713.9
Unusual Observations
Obs x y
Fit SE Fit
Residual St Resid
1 3.0
5.000 6.541 1.627
-1.541 -0.55 X
2 7.0
11.000 10.155 1.440
0.845 0.29 X
3 11.0
21.000 13.770 1.258
7.230 2.43R
11 31.0
40.000 31.843 0.575
8.157 2.57R
R denotes an observation with a large standardized residual.
X denotes an observation whose X value gives it large leverage.
Ejercicios de repaso
11.43 Los siguientes datos
son el resultado de una investigación sobre el efecto de la temperatura de
reacción x, sobre la conversión porcentual
de un proceso químico y. Haga un ajuste por regresión lineal simple y utilice
pruebas de falta de ajuste para determinar si el modelo es adecuado. Analice
los resultados.
|
Observación |
Temperatura (°C) x |
Conversión % y |
|
1 |
200 |
43 |
|
2 |
250 |
78 |
|
3 |
200 |
69 |
|
4 |
250 |
73 |
|
5 |
189.65 |
48 |
|
6 |
260.35 |
78 |
|
7 |
225 |
65 |
|
8 |
225 |
74 |
|
9 |
225 |
76 |
|
10 |
225 |
79 |
|
11 |
225 |
83 |
|
12 |
225 |
81 |
11.48 Para una variedad
particular de planta, los investigadores desean desarrollar una formula para
predecir la cantidad de semillas (granos) como función de la densidad de las
plantas. Efectuaron un estudio con cuatro niveles del factor X, el número de
plantas por parcela. Se utilizaron cuatro réplicas para cada nivel de X. A
continuación se muestran los datos.
|
Plantas por parcela x |
Cantidad de semillas y (granos) |
|
10 |
12.6,
11.0, 12.1, 10.9 |
|
20 |
15,3,
16.1, 14.9, 15.6 |
|
30 |
17.9,
18.3, 18.6, 17.8 |
|
40 |
19.2,
19.6, 18.9, 20.0 |
¿Es adecuado un modelo
de regresión lineal para analizar el conjunto de datos?
Bibliografía.
[Walpole et all] Walpole Ronald
E., Myers Raymond H., Myers Sharon L. y Ye Keying “Probabilidad y
estadística para Ingeniería y ciencias”. Octava Edición. Pearson Education. 2007.