7. Modelo de regresión lineal con el uso de matrices.

Al ajustar un modelo de regresión lineal múltiple, en particular cuando el número de variable pasa de dos, el conocimiento de la teoría matricial puede facilitar las manipulaciones matemáticas. Supongamos que el experimentador tiene x₁, x₂, ..., x_k variables independientes y n observaciones y₁, y₂, .. y_n.

En forma compacta podemos escribir como

donde

El sistema de ecuaciones a resolver es Xb=y y la solución por mínimos cuadrados es:

Análisis de varianza de regresión múltiple.

Se puede llevar a cabo un análisis de varianza para aclarar la calidad de la ecuación de regresión. Una hipótesis útil que determina si un modelo depende linealmente de un conjunto de variables es

H₀: b₁ = b₂ = ... = b_k = 0

Análisis de variancia para probar b₁ = b₂ = ... = b_k = 0
Fuente de variación	Suma de cuadrados	Grados de libertad	Cuadrado medio	f calculada
Regresión	SSR	k	s₁ =SSR/k	s₁/s₂
Error	SSE	n-(k+1)	s₂=SSE/ (n-(k+1))
Total	SST	n-1
rechazamos H₀, al nivel de significancia a cuando f > f_a(k, n-(k+1))

Ejemplo 6.

Se midió el porcentaje de sobre vivencia de cierto tipo de semen animal, después del almacenamiento, en varias combinaciones de concentraciones de tres materiales que se utilizan para aumentar su oportunidad de sobre vivencia. Los datos son:

x1 (peso %)	x2 (peso %)	x3 (peso %)	y (% sobre vivencia)
1.74	5.3	10.8	25.5
6.32	5.42	9.4	31.2
6.22	8.41	7.2	25.9
10.52	4.63	8.5	38.4
1.19	11.6	9.4	18.4
1.22	5.85	9.9	26.7
4.1	6.62	8	26.4
6.32	8.72	9.1	25.9
4.08	4.42	8.7	32
4.15	7.6	9.2	25.2
10.15	4.83	9.4	39.7
1.72	3.12	7.6	35.7
1.7	5.3	8.2	26.5

Determinar el modelo lineal y verifique, utilizando análisis de varianza que efectivamente el modelo depende linealmente de la variables propuestas.

Curva ajustada

b = [b₀, b₁, b₂, b₃]

b = [39.1573, 1.0161, -1.8616, -0.3433]

---------------------------------------------------------------------

Análisis de Varianza

---------------------------------------------------------------------

Fuente de Suma Grados de Cuadrado F calc

Variación cuadrados Libertad medio

---------------------------------------------------------------------

Regresión 399.45 3 133.15 30.98

Error 38.68 9 4.30

Total 438.13 12

---------------------------------------------------------------------

Con (1-alfa) = 0.950 tenemos 30.98 > 3.86

Para llevar a cabo el ajuste se corrió el siguiente código en MATLAB

clear;

x = [

1.74 5.30 10.80;

6.32 5.42 9.40;

6.22 8.41 7.20;

10.52 4.63 8.50;

1.19 11.60 9.40;

1.22 5.85 9.90;

4.10 6.62 8.00;

6.32 8.72 9.10;

4.08 4.42 8.70;

4.15 7.60 9.20;

10.15 4.83 9.40

1.72 3.12 7.60;

1.70 5.30 8.20];

y = [ 25.5; 31.2; 25.9; 38.4; 18.4; 26.7; 26.4; 25.9; 32.0; 25.2; 39.7; 35.7; 26.5];

n = length(x(:,1));

k = length(x(1,:));

[SSE, SSR, b] = modelo(x, y, [1 2 3]);

SST = SSE + SSR;

v1 = k;

v2 = n-k-1;

s2 = SSE/(n-k-1);

F = (SSR/k)/s2

alfa = 0.05;

Fc = finv(1-alfa, v1, v2);

fprintf('---------------------------------------------------------------------\n');

fprintf('Curva ajustada\n');

display (b)

fprintf('---------------------------------------------------------------------\n');

fprintf('Analisis de Varianza\n');

fprintf('---------------------------------------------------------------------\n');

fprintf('Fuente de Suma Grados de Cuadrado F calc\n');

fprintf('Variacion cuadrados Libertad medio \n');

fprintf('---------------------------------------------------------------------\n');

fprintf('Regresion %13.2f %13.f %13.2f %13.2f\n', SSR, v1, SSR/v1, F);

fprintf('Error %13.2f %13.f %13.2f \n', SSE, v2, s2);

fprintf('Total %13.2f %13.f \n', SST, v1+v2);

fprintf('---------------------------------------------------------------------\n');

fprintf('Con (1-alfa) = %5.3f tenemos %13.2f > %13.2f\n', 1-alfa, F, Fc);

El programa para el cálculo del modelo multivariado es:

function [SSE, SSR, b] = modelo(x, y, campos)

K = length(x(1, :));

X = ones(length(x(:,1)),1);

for m = 1: length(campos)

X = [X, x(:,campos(m))];

end;

b = inv(X'*X)*X'*y;

SSE = (X*b-y)'*(X*b-y);

yp = mean(y);

SSR = (X*b-yp)'*(X*b-yp);

b = inv(X'*X)*X'*y;

SSE = (X*b-y)'*(X*b-y);

yp = mean(y);

SSR = (X*b-yp)'*(X*b-yp);

La solución utilizando MINITAB es:

Results for: semen_animal.MTW

Regression Analysis: y versus x1, x2, x3

The regression equation is

y = 39.2 + 1.02 x1 - 1.86 x2 - 0.343 x3

Predictor Coef SE Coef T P

Constant 39.157 5.887 6.65 0.000

x1 1.0161 0.1909 5.32 0.000

x2 -1.8616 0.2673 -6.96 0.000

x3 -0.3433 0.6171 -0.56 0.592

S = 2.07301 R-Sq = 91.2% R-Sq(adj) = 88.2%

Analysis of Variance

Source DF SS MS F P

Regression 3 399.45 133.15 30.98 0.000

Residual Error 9 38.68 4.30

Total 12 438.13

Source DF Seq SS

x1 1 187.31

x2 1 210.81

x3 1 1.33

Unusual Observations

Obs x1 y Fit SE Fit Residual St Resid

5 1.2 18.400 15.545 1.579 2.855 2.13R

12 1.7 35.700 32.488 1.465 3.212 2.19R

R denotes an observation with a large standardized residual.

De la prueba de hipótesis utilizando MINITAB podemos ver que el valor de P es 0.000 lo cual indica que para nuestro nivel de significancia de 0.05 estamos por arriba de este valor y la hipótesis se rechaza. Esto significa que hay suficiente evidencia de dependencia lineal.

8.- Elección de un modelo de ajuste a través de pruebas de Hipótesis.

El experimentador que utiliza el análisis de regresión también se interesa en la supresión de variables cuando la situación dicta que, además de llegar a una ecuación de predicción más fácil de trabajar, debe de encontrar la mejor regresión que incluya las mejores variables de pronóstico.

Un criterio que por lo general se utiliza para ilustrar lo adecuado de un modelo de regresión es el coeficiente de determinación múltiple:

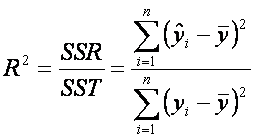
Esta cantidad nos da una idea de la calidad del modelo propuesto.

La inclusión de cualquier variable única en un sistema de regresión aumentará la suma de cuadrados de regresión y por ello reducirá la suma de cuadrados del error. En consecuencia debemos decidir si el aumento en la regresión es suficiente para garantizar su uso en el modelo.

Prueba T.

Inicialmente podemos probar

H₀ : b_j = 0

H₁ : b_j es diferente de cero

con el uso de la distribución t con v grados de libertad. Tenemos

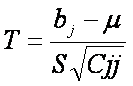
donde :

b_j => es la variable que deseamos probar respecto a un valor dado m

S => es la varianza dada por sqrt(SSE/(n-k-1)) y

C_ii => es el elemento en la diagonal j de la matriz de covarianzas.

y aceptamos la hipótesis H₀, si -t_a_/2< T < t_a_/2

La matriz de covarianza se calcula como

También podemos probar si la variable independiente depende de una x₃, haciendo análisis de varianza. En este caso definamos la suma de cuadrados de regresión considerando todas las variables como:

R(b₁,b₂,b₃) = SSR

y la suma de cuadrados de regresión sin una variable (por ejemplo sin 3) como:

R(b₁,b₂) = SSR_1,2

Ejemplo 7.

Para los datos del ejemplo 6 determinar si la variable x₃ contribuye significativamente al modelo. Solución, tenemos:

SSE = 38.6764

SSR = 399.4544

b = [ 39.1573, 1.0161, -1.8616, -0.3433]

| 1.0 1.74 5.30 10.80 |

| 1.0 6.32 5.42 9.40 |

| 1.0 6.22 8.41 7.20 |

| 1.0 10.52 4.63 8.50 |

| 1.0 1.19 11.60 9.40 |

| 1.0 1.22 5.85 9.90 |

X = | 1.0 4.10 6.62 8.00 |

| 1.0 6.32 8.72 9.10 |

| 1.0 4.08 4.42 8.70 |

| 1.0 4.15 7.60 9.20 |

| 1.0 10.15 4.83 9.40 |

| 1.0 1.72 3.12 7.60 |

| 1.0 1.70 5.30 8.20 |

Cov = inv(X^TX)

Cov =

8.0648 -0.0826 -0.0942 -0.7905

-0.0826 0.0085 0.0017 0.0037

-0.0942 0.0017 0.0166 -0.0021

-0.7905 0.0037 -0.0021 0.0886

S² = SSE/(n-k-1) = 38.6764/(13-3-1) = 4.2973777

Sustituyendo en la formula tenemos

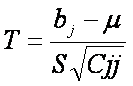
T = (-0.3433 – 0)/sqrt(4.297377* 0.0886)

T = -0.556

Por lo tanto, para X3 -2.821 < -0.556 < 2.821

Existe suficiente evidencia para aceptar la Hipótesis H₀, lo cual significa, rechazar la variable x₃ del modelo.

De los resultados de MINITAB podemos ver este mismo resultado. La columna T corresponde al estadístico calculado con este procedimiento y P es el porcentaje de significancia para T. Podemos ver que el termino independiente y las variables x1 y x2 tienen un valor P de 0.000 muy inferior a nuestro nivel de significancia de 0.05 mientras que x3 es superior. Por lo tanto el modelo no depende de la variable x3.

Predictor Coef SE Coef T P

Constant 39.157 5.887 6.65 0.000

x1 1.0161 0.1909 5.32 0.000

x2 -1.8616 0.2673 -6.96 0.000

x3 -0.3433 0.6171 -0.56 0.592

Intervalo de confianza

Un intervalo de confianza de (1-a)100% para la respuesta media m_y|x1_,x2,…xk es

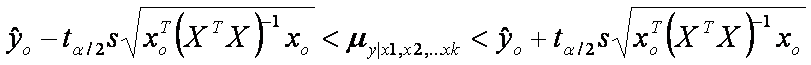
donde t_a_/2 es un valor de la distribución t con n-k-1 grados de libertad.

Ejemplo

Con los datos del ejemplo anterior, construya un intervalo de confianza de 95% para la respuesta media cuando x1 = 3%, x2 = 8% y x3 = 9%.

La ecuación de regresión calculada es

y = 39.2 + 1.02 x1 - 1.86 x2 - 0.343 x3

sustituyendo los valores tenemos

y = 39.2 + 1.02 (3) - 1.86 (8) - 0.343 (9) = 24.2232

Determinamos el valor

x_o'(X’X)^-1x_o =

[1 3 8 9 ] *

| 8.0648 -0.0826 -0.0942 -0.7905 | | 1 |

| -0.0826 0.0085 0.0017 0.0037 | | 3 |

| -0.0942 0.0017 0.0166 -0.0021 | | 8 |

| -0.7905 0.0037 -0.0021 0.0886 | | 9 |

x_o'(X’X)^-1x_o = 0.1267

s² = 4.298 o s =2.073

t_a_/2 = 2.262

24.2232 – (2.262)(2.073)sqrt(0.1267) < m < 24.2232 +(2.262)(2.073) sqrt(0.1267)

22.5541 < m < 25.8923

Prueba F.

La cantidad de variación en la respuesta debido a la eliminación de 3 en presencia de 1 y de, la definimos como:

R(b₃|b₁,b₂) = R(b₁,b₂,b₃)- R(b₁,b₂)

R(b₃|b₁,b₂) = SSR_1,2,3 – SSR_1,2

Entonces para probar la hipótesis

H₀ : b₃ = 0

H₁ : b₃ diferente de cero

calculamos

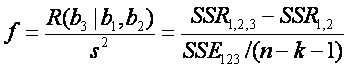
y rechazamos la hipótesis, al nivel de significancia alfa, si fa (1,n-k-1) < f

Ejemplo 8.

Repetir el ejemplo 7 utilizando análisis de varianza.

SSR123 = 399.4544

SSE123 = 38.6764

SSR12 = 398.1245

SSE12 = 40.0063

S = SSE123/(n-k-1) = 38.6764/(13-3-1) = 4.2973

f = (399.4544 - 398.1245)/4.2973 =0.3094

fcal = finv(0.98,1, n-k-1) = 7.961

Por lo tanto, la prueba f para X₃, da 7.961 < 0.309. Se acepta la Hipótesis H₀, lo cual significa que el modelo no depende de X₃.

La implementación de estas rutinas en MATLAB queda como:

clear;

x = [

1.74 5.30 10.80;

6.32 5.42 9.40;

6.22 8.41 7.20;

10.52 4.63 8.50;

1.19 11.60 9.40;

1.22 5.85 9.90;

4.10 6.62 8.00;

6.32 8.72 9.10;

4.08 4.42 8.70;

4.15 7.60 9.20;

10.15 4.83 9.40

1.72 3.12 7.60;

1.70 5.30 8.20];

y = [ 25.5; 31.2; 25.9; 38.4; 18.4; 26.7; 26.4; 25.9; 32.0; 25.2; 39.7; 35.7; 26.5];

[SSE, SSR, b] = modelo(x, y, [1 2 3])

n = length(x(:,1));

k = length(x(1,:)) + 1;

v1 = k;

v2 = n-k-1;

S = sqrt(SSE/(n-k-1));

Cov =inv([ones(length(x(:,1)),1), x]'*[ones(length(x(:,1)),1), x])

Tc = Tinv(0.99, v2);

Fc = Finv(0.98, 1, v2);

mods= [2 3; 1 3; 1 2]

for m = 2:k+1;

T = b(m)/S/sqrt(Cov(m,m));

[SSE_r, SSR_r, b_r] = modelo(x, y, mods(m-1,:));

F = (SSR - SSR_r)/S/S

fprintf('prueba (t)para X%d %10.3f < %10.3f < %10.3f \n', m-1, -Tc, T, Tc);

fprintf('prueba (f)para X%d %10.3f < %10.3f \n', m-1, Fc, F);

end;

9. Regresión por pasos.

Un procedimiento para buscar el “subconjunto óptimo” de variables es una técnica que se llama regresión por pasos. Se basa en el procedimiento de introducir en forma secuencial las variables al modelo una por una. Existen dos maneras de llevar a cabo este procedimiento

a) selección hacia delante

b) Eliminación hacia atrás.

Selección hacia delante.

El procedimiento es el siguiente

Paso 1: Elegir la variable que de la suma de cuadrados de la regresión (SSR) más grande cuando se lleva a cabo la regresión lineal simple con y o, de manera equivalente la que de el valor más alto de R². Llamaremos a esta variable inicial x₁.

Paso 2: Elegir la variable que cuando se introduce en el modelo da el mayor incremento R² en presencia de la variable x₁

SSRj|1 = SSR1j – SSR1

por supuesto elegimos a la R mas grande y llamamos a esta la variable x₂.

Paso 3: Elegir la variable x_j que de el valor más grande de

SSRj|12 = SSR12j – SSR12

Este proceso se continúa hasta que la variable introducida más reciente deje de inducir un aumento significativo en la regresión. Tal incremento puede determinar en cada paso con el uso de la prueba F o prueba t apropiada. Por ejemplo en el paso 2 el valor

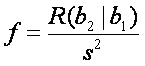
se puede determinar para probar lo apropiado del modelo. Aquí el valor de s² es el cuadrado medio del error para el modelo que contiene las variables b₂ y b₁

La prueba de hipótesis que probamos en este caso es:

H₀ : R(b_j|b) = 0

H₁ : R(b_j|b) es diferente de cero

calculamos el valor de f y rechazamos la hipótesis nula, en un nivel de significancia a, si f > f_a(1, n-1-k), donde k es el número de modelos introducidos.

Análisis de variancia para probar R(b_j\|b) = 0
Fuente de variación	Suma de cuadrados	Grados de libertad	Cuadrado medio	f calculada
Regresión	SSR(b_j,b)	1	s₁ =SSR(bj,b)-SSR(b)	s₁/s₂
Error	SSE(b_j,b)	n-k-1	s₂=SSE(bj,b)/ (n-k-1)
Total	SST(b_j,b)	n-k
rechazamos H₀, al nivel de significancia a cuando f > f_a(1, n-k-1)

Solución con MINITAB

Para llevar a cabo este procedimiento en MINITAB ir al menú Stat > Regression > Stepwise

Después de seleccionar esta opción aparecerá la caja de dialogo

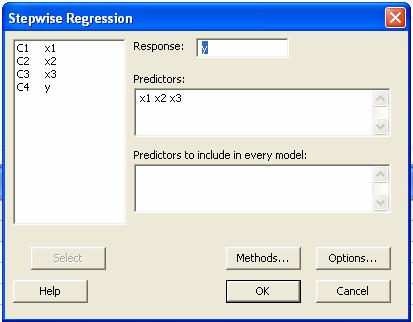
Donde hay que poner la Respuesta en este caso la columna C4 o y y los predoctores x1, x2 y x3.

Ejemplo 9.

Considere los datos de la siguiente tabla, donde se tomaron mediciones de nueve niños. El propósito del experimento fue llegar a una ecuación de estimación adecuada que relacionara la estatura de un niño con todas o un subconjunto de variables independientes. Encuentre el modelo lineal utilizando regresión por selección hacia adelante.

Edad	Estatura al nacer	Peso al nacer	Talla del tórax al nacer	Estatura del niño
x1 (días)	x2 (cm)	x3 (kg)	x4 (cm)	y (cm)
78.00	48.20	2.75	29.50	57.50
69.00	45.50	2.15	26.30	52.80
77.00	46.30	4.41	32.20	61.30
88.00	49.00	5.52	36.50	67.00
67.00	43.00	3.21	27.20	53.50
80.00	48.00	4.32	27.70	62.70
74.00	48.00	2.31	28.30	56.20
94.00	53.00	4.30	30.30	68.50
102.00	58.00	3.71	28.70	69.20

Comenzaremos por analizar el ingreso de las variables 1, 2, 3 y 4 por separado.

---------------------------------------------------------------------

Analisis de Varianza y = 19.01 + 0.52 * X(1)

---------------------------------------------------------------------

Fuente de Suma Grados de Cuadrado F calc

Variacion cuadrados Libertad medio

---------------------------------------------------------------------

Regresion 288.15 1 288.15 60.95

Error 33.09 7 4.73

Total 321.24 8

---------------------------------------------------------------------

Con (1-alfa) = 0.990 tenemos 60.95 > 5.59

R(bj|b) = SSR(bj U b) - SSR(b) = 288.15 R^2 = 0.89698

---------------------------------------------------------------------

Analisis de Varianza y = 3.43 + 1.18 * X(2)

---------------------------------------------------------------------

Fuente de Suma Grados de Cuadrado F calc

Variacion cuadrados Libertad medio

---------------------------------------------------------------------

Regresion 215.30 1 215.30 14.23

Error 105.94 7 15.13

Total 321.24 8

---------------------------------------------------------------------

Con (1-alfa) = 0.990 tenemos 14.23 > 5.59

R(bj|b) = SSR(bj U b) - SSR(b) = 215.30 R^2 = 0.67022

---------------------------------------------------------------------

Analisis de Varianza y = 45.30 + 4.31 * X(3)

---------------------------------------------------------------------

Fuente de Suma Grados de Cuadrado F calc

Variacion cuadrados Libertad medio

---------------------------------------------------------------------

Regresion 186.11 1 186.11 9.64

Error 135.13 7 19.30

Total 321.24 8

---------------------------------------------------------------------

Con (1-alfa) = 0.990 tenemos 9.64 > 5.59

R(bj|b) = SSR(bj U b) - SSR(b) = 186.11 R^2 = 0.57934

---------------------------------------------------------------------

Analisis de Varianza y = 27.19 + 1.14 * X(4)

---------------------------------------------------------------------

Fuente de Suma Grados de Cuadrado F calc

Variacion cuadrados Libertad medio

---------------------------------------------------------------------

Regresion 100.86 1 100.86 3.20

Error 220.38 7 31.48

Total 321.24 8

---------------------------------------------------------------------

Con (1-alfa) = 0.990 tenemos 3.20 > 5.59

R(bj|b) = SSR(bj U b) - SSR(b) = 100.86 R^2 = 0.31397

En resumen

R(b1|[]) = SSR(b1) - SSR([]) = 288.15 R^2 = 0.89698

R(b2|[]) = SSR(b2) - SSR([]) = 215.30 R^2 = 0.67022

R(b3|[]) = SSR(b3) - SSR([]) = 186.11 R^2 = 0.57934

R(b4|[]) = SSR(b4) - SSR([]) = 100.86 R^2 = 0.31397

Podemos concluir que la variable más significativa es : X1. Con un grado de significancia de 0.01 tenemos :

Con (1-alfa) = 0.990 tenemos 60.95 > 5.59

Una vez introducida la variable X1 continuamos nuestro análisis con X2, X3 y X4.

---------------------------------------------------------------------

Analisis de Varianza y = 44.10 + 0.98 * X(1) -1.29 * X(2)

---------------------------------------------------------------------

Fuente de Suma Grados de Cuadrado F calc

Variacion cuadrados Libertad medio

---------------------------------------------------------------------

Regresion 312.02 1 312.02 15.53

Error 9.22 6 1.54

Total 321.24 7

---------------------------------------------------------------------

Con (1-alfa) = 0.990 tenemos 15.53 > 5.99

R(bj|b) = SSR(bj U b) - SSR(b) = 23.87 R^2 = 0.97129

---------------------------------------------------------------------

Analisis de Varianza y = 20.11 + 0.41 * X(1) + 2.03 * X(3)

---------------------------------------------------------------------

Fuente de Suma Grados de Cuadrado F calc

Variacion cuadrados Libertad medio

---------------------------------------------------------------------

Regresion 317.46 1 317.46 46.47

Error 3.78 6 0.63

Total 321.24 7

---------------------------------------------------------------------

Con (1-alfa) = 0.990 tenemos 46.47 > 5.99

R(bj|b) = SSR(bj U b) - SSR(b) = 29.31 R^2 = 0.98822

---------------------------------------------------------------------

Analisis de Varianza y = 9.32 + 0.47 * X(1) + 0.46 * X(4)

---------------------------------------------------------------------

Fuente de Suma Grados de Cuadrado F calc

Variacion cuadrados Libertad medio

---------------------------------------------------------------------

Regresion 301.96 1 301.96 4.30

Error 19.28 6 3.21

Total 321.24 7

---------------------------------------------------------------------

Con (1-alfa) = 0.990 tenemos 4.30 > 5.99

R(bj|b) = SSR(bj U b) - SSR(b) = 13.82 R^2 = 0.94000

R(b2|b1) = SSR(b2,b1) - SSR(b1) = 23.87 R^2 = 0.97129

R(b3|b1) = SSR(b2,b1) - SSR(b1) = 29.31 R^2 = 0.98822

R(b4|b1) = SSR(b3,b1) - SSR(b1) = 13.82 R^2 = 0.94000

Podemos concluir que la variable más significativa dada X1 es X3, con un grado de significancia de 0.01 tenemos:

Con (1-alfa) = 0.990 tenemos 46.47 > 5.99

Finalmente analizamos la introducción de las variables 2 y 4 dado que X1 y X3 forman parte del modelo.

---------------------------------------------------------------------

Analisis de Varianza y = 5.63 + 0.08 * X(1) + 3.07 * X(3) + 0.77 * X(2)

---------------------------------------------------------------------

Fuente de Suma Grados de Cuadrado F calc

Variacion cuadrados Libertad medio

---------------------------------------------------------------------

Regresion 318.25 1 318.25 1.33

Error 2.99 5 0.60

Total 321.24 6

---------------------------------------------------------------------

Con (1-alfa) = 0.990 tenemos 1.33 > 6.61

R(bj|b) = SSR(bj U b) - SSR(b) = 0.79 R^2 = 0.99069

---------------------------------------------------------------------

Analisis de Varianza y = 21.87 + 0.41 * X(1) + 2.20 * X(3) -0.08 * X(4)

---------------------------------------------------------------------

Fuente de Suma Grados de Cuadrado F calc

Variacion cuadrados Libertad medio

---------------------------------------------------------------------

Regresion 317.64 1 317.64 0.26

Error 3.60 5 0.72

Total 321.24 6

---------------------------------------------------------------------

Con (1-alfa) = 0.990 tenemos 0.26 > 6.61

R(bj|b) = SSR(bj U b) - SSR(b) = 0.19 R^2 = 0.98880

R(b2|b1, b3) = SSR(b1, b2, b3) - SSR(b1, b3) = 0.79 R^2 = 0.99069

R(b4|b1, b3) = SSR(b1, b3, b4) - SSR(b1, b3) = 0.19 R^2 = 0.98880

En este caso podemos notar que ninguna de las dos variables introduce un incremento significante y con un grado de significancia de 0.01 podemos no tomar en cuenta su efecto dado que:

Con (1-alfa) = 0.990 tenemos 1.33 > 6.61

Con (1-alfa) = 0.990 tenemos 0.26 > 6.61

Finalmente nuestro modelo es: y = 20.11 + 0.41 * X(1) + 2.03 * X(3)

La implementación de este algoritmo en MATLAB es:

function z =regresion(x, y, mod, SSR_old)

[SSE, SSR, b] = modelo(x, y, mod);

v1 = 1;

v2 = length(y)-1-length(mod);

R = SSR - SSR_old;

F = R/(SSE/v2);

s2 = SSE/v2;

SST = SSE + SSR;

Fc = finv(0.95, v1, v2);

alfa = 0.01;

fprintf('---------------------------------------------------------------------\n');

fprintf('Analisis de Varianza');

fprintf(' y = %5.2f', b(1));

for m = 1:length(mod)

if(b(m+1)>=0), fprintf(' + %5.2f * X(%d)', b(m+1), mod(m))

else fprintf(' %5.2f * X(%d)', b(m+1), mod(m))

end;

fprintf('\n');

fprintf('---------------------------------------------------------------------\n');

fprintf('Fuente de Suma Grados de Cuadrado F calc\n');

fprintf('Variacion cuadrados Libertad medio \n');

fprintf('---------------------------------------------------------------------\n');

fprintf('Regresion %13.2f %13.f %13.2f %13.2f\n', SSR, v1, SSR/v1, F);

fprintf('Error %13.2f %13.f %13.2f \n', SSE, v2, s2);

fprintf('Total %13.2f %13.f \n', SST, v1+v2);

fprintf('---------------------------------------------------------------------\n');

fprintf('Con (1-alfa) = %5.3f tenemos %13.2f > %13.2f\n', 1-alfa, F, Fc);

fprintf('R(bj|b) = SSR(bj U b) - SSR(b) = %13.2f R^2 = %13.5f\n', R, SSR/SST);

%fprintf(' SSE SSR R s2 F Fcalc\n');

%fprintf('%10.3f %10.3f %10.3f %10.3f %10.3f %10.3f\n', SSE, SSR, R, SSE/v2, f, fcal);

z = SSR;

fprintf('\n \n');

La solución con MINITAB es :

Results for: talla_ninos.MTW

Stepwise Regression: Estatura versus Edad, Est al nacer, ...

Alpha-to-Enter: 0.15 Alpha-to-Remove: 0.15

Response is Estatura on 4 predictors, with N = 9

Step 1 2

Constant 19.01 20.11

Edad 0.518 0.414

T-Value 7.81 14.43

P-Value 0.000 0.000

Peso al nacer 2.03

T-Value 6.82

P-Value 0.000

S 2.17 0.794

R-Sq 89.70 98.82

R-Sq(adj) 88.23 98.43

Mallows Cp 39.6 2.1

El estadístico Cp

El estadístico Cp es una función sencilla del número total de parámetros en el modelo candidato y el error cuadrático medio s². Resulta que los mejores conjuntos de variables serán aquellos que tengan el estadístico Cp. Para hacer esta prueba utilizaremos MINITAB en el menú Stat > Regression > Best Subsets …

Dar los parámetros en la caja de dialogo

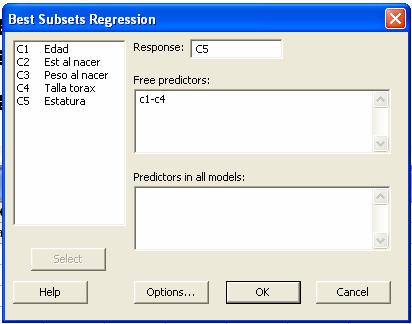
Los resultados para el ejemplo 9 son:

Best Subsets Regression: Estatura versus Edad, Est al nacer, ...

Response is Estatura

E e

s s T

t o a

a a l

l l a

n n t

E a a o

d c c r

Mallows a e e a

Vars R-Sq R-Sq(adj) Cp S d r r x

1 89.7 88.2 39.6 2.1743 X

1 67.0 62.3 137.9 3.8903 X

2 99.1 98.7 1.1 0.71138 X X

2 98.8 98.4 2.1 0.79420 X X

3 99.1 98.5 3.0 0.77327 X X X

3 99.1 98.5 3.1 0.77845 X X X

4 99.1 98.2 5.0 0.86104 X X X X

Podemos ver que las variables Estatura al nacer y peso a nacer tienen el menor Cp, por lo tanto el modelo solamente dependerá de estas dos variables para esta prueba.

Ejercicios de repaso

12.14 Veintitrés estudiantes de pedagogía tomaron parte en un programa de evaluación diseñado para medir la eficacia de los profesores y determinar que factores son importantes. Participaron 11 instructoras. La medición de la respuesta fue una evaluación cuantitativa del maestro colaborador. Las variables regresoras fueron las calificaciones de cuatro pruebas estandarizadas entregadas a cada instructor. Los datos son los siguientes.

y	x1	x2	x3	x4
410	69	125	59.00	55.66
569	57	131	31.75	63.97
425	77	141	80.50	45.32
344	81	122	75.00	46.67
324	0	141	49.00	41.21
505	53	152	49.35	43.83
235	77	141	60.75	41.61
501	76	132	41.25	64.57
400	65	157	50.75	42.41
584	97	166	32.25	57.95
434	76	141	54.50	57.90

a) Hacer el modelo de regresión y calcular la línea de mínimos cuadrados

b) Hacer un análisis de varianza y decir si el modelo es adecuado

c) Hacer pruebas T a cada una de las variables del modelo

d) Construya un intervalo de confianza de 95% para la respuesta media cuando x1 = 80, x2 = 110, x3 = 70 y x4 = 53 utilizando todas las variables del modelo.

e) Calcular el modelo de regresión por pasos

f) Decir el mejor conjunto de variables utilizando el criterio Cp.

12.54 En un esfuerzo para modelar las remuneraciones de los ejecutivos en el año de 1979, se seleccionaron 33 empresas y se recabaron datos acerca de remuneraciones ventas, ganancias y empleo. Considere el modelo

y_i =b₀ + b₁ ln x_1,i+ b₁ ln x_2,i+ b₁ ln x_3,i

a) ajuste el modelo anterior

b) Cual es el valor de la compensación con x1 = 10,000, x2 = 100 y x3 = 50.

c) Existe un intervalo de confianza para y con los datos de b

Compensación y (miles)	Ventas x1 (millones)	Ganancias x2 (millones)	Empleo x3
450	4600.6	128.1	48000
387	9255.4	783.9	55900
368	1526.2	136.0	13783
277	1683.2	179.0	27765
676	2752.8	231.5	34000
454	2205.8	329.5	26500
507	2384.6	381.8	30800
496	2746.0	237.9	41000
487	1434.0	222.3	25900
383	470.6	63.7	8600
311	1508.0	149.5	21075
271	464.4	30.0	6874
524	9329.3	577.3	39000
498	2377.5	250.7	34300
343	1174.3	82.6	19405
354	409.3	61.5	3586
324	724.7	90.8	3905
225	578.9	63.3	4139
254	966.8	42.8	6255
208	591.0	48.5	10605
518	4933.1	310.6	65392
406	7613.2	491.6	89400
332	3457.4	228.0	55200
340	545.3	54.6	7800
698	22862.8	3011.3	337119
306	2361.0	203.0	52000
613	2614.1	201.0	50500
302	1013.2	121.3	18625
540	4560.3	194.6	97937
293	855.7	63.4	12300
528	4211.6	352.1	71800
456	5440.6	655.2	87700
417	1229.9	97.5	14600

Bibliografía.

[Walpole et all] Walpole Ronald E., Myers Raymond H., Myers Sharon L. y Ye Keying “Probabilidad y estadística para Ingeniería y ciencias”. Octava Edición. Pearson Education. 2007.

Regresar.

Análisis de variancia para probar b1 = b2 = ... = bk = 0

H1 : R(bj|b) es diferente de cero

Análisis de variancia para probar R(bj|b) = 0

SSR(bj,b)

Ejemplo 9.

R(b1|[]) = SSR(b1) - SSR([]) = 288.15 R^2 = 0.89698

R(b3|b1) = SSR(b2,b1) - SSR(b1) = 29.31 R^2 = 0.98822

Análisis de variancia para probar b₁ = b₂ = ... = b_k = 0

H₁ : R(b_j|b) es diferente de cero

Análisis de variancia para probar R(b_j|b) = 0

SSR(b_j,b)