Diseño de experimentos.

1. Análisis de varianza.

Suponga que un experimento industrial un ingeniero está interesado en cómo la absorción media de humedad en concreto varía entre cinco mezclas diferentes de concreto. Las muestras se exponen a la humedad por 48 horas y se decide que se prueben seis muestras para cada mezcla, por lo que se requiere probar un total de 30 muestras. Los datos de este experimento se muestran en la siguiente tabla.

Tabla 1

Absorción de humedad en mezclas de concreto.
Mezcla	1	2	3	4	5
	551.00	595.00	639.00	417.00	563.00
	457.00	580.00	615.00	449.00	631.00
	450.00	508.00	511.00	517.00	522.00
	731.00	583.00	573.00	438.00	613.00
	499.00	633.00	648.00	415.00	656.00
	632.00	517.00	677.00	555.00	679.00
Total	3320.00	3416.00	3663.00	2791.00	3664.00	16854.00
Media	553.33	569.33	610.50	465.17	610.67	561.80

El modelo para esta estimación se puede considerar como sigue. Hay 6 observaciones que se toman cada una de las cinco poblaciones con medias m₁, m₂,..m₅ respectivamente y deseamos probar

H₀ : m₁ = m₂ = m₃ = m₄ = m₅

H₁ : al menos dos de las medias no son iguales.

Además, nos podemos interesar en realizar comparaciones individuales entres estas cinco medias poblacionales.

En el procedimiento de análisis de varianza, se supone que cualquier variación que exista entre los promedios de las mezclas se atribuye a

1) La variación en la absorción entre las observaciones dentro de los tipos de mezclas

2) la variación que se debe a los tipos de mezclas; las que se deben a diferencias en la composición química de las mezclas.

Las variaciones dentro de la muestra, por supuesto, son ocasionadas por diversas causas. Quizá las condiciones de humedad y temperatura no se conservaron completamente constantes a lo largo del experimento. Es posible que haya cierta cantidad de heterogeneidad en los lotes de materia prima que se utilizan. De todos modos, consideraremos que la variación dentro de la muestra es una variación aleatoria o al azar, y parte del objetivo del análisis de varianza es determinar si las diferencias entre las cinco medias muéstrales son las que se esperarían debido sólo a la variación aleatoria o si en realidad también hay una contribución de la variación sistemática que se atribuye al tipo de mezcla.

2. Estrategia del diseño experimental.

Definimos a una unidad experimental como una unidad motivo del análisis, por ejemplo, una unidad experimental podría ser el peso, la talla, el nivel de colesterol, etc. Es necesario que estas se tomen de forma aleatoria para eliminar el sesgo, nunca se debe realizar el experimento para un conjunto de variables dadas y tomar de forma secuencial un conjunto de datos.

Cuando se tiene un conjunto de datos grande el sesgo se reduce, pero hay que recordar, que este se incrementa a medida que reducimos el tamaño del conjunto.

Definimos un bloque al conjunto de unidades experimentales que se agrupan de acuerdo a una propiedad o característica en particular. Los niveles del factor o tratamiento se asignan entonces de forma aleatoria dentro de los bloques. El propósito de formar bloques es reducir el error experimental efectivo.

El término tratamiento se usa por lo general para referirnos a las diversas clasificaciones, ya sea de las mezclas diferentes, análisis diferentes, fertilizantes diferentes o regiones diferentes del país.

3. Diseño completamente aleatorizado.

Se seleccionan muestras aleatorias de tamaño n de cada una de las k poblaciones. Las k poblaciones diferentes se clasifican sobre la base de un solo criterio, como tratamientos o grupos diferentes. Se supone que las k poblaciones son diferentes y normalmente distribuidas con medias m₁, m₂, ..m_k y varianza común s²

Deseamos derivar métodos apropiados para probar la hipótesis

H₀ : m₁ = m₂ = m₃ = m₄ = m₅

H₁ : al menos dos de las medias no son iguales.

Denotemos a y_ij como la j-ésima observación del i-ésimo tratamiento y acomodemos los datos de acuerdo con la siguiente tabla.

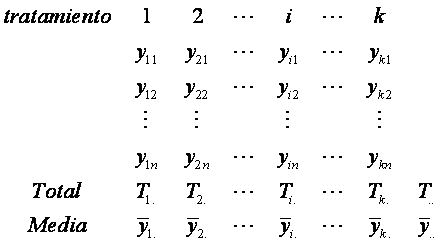
Aquí T_i es el total de todas las observaciones del i-ésimo tratamiento, es la media de todas las observaciones del i-ésimo tratamiento, T_. es el total de las nk observaciones y es la media de todas las observaciones. Cada observación se puede escribir en la forma

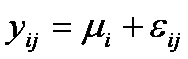
donde e_ij mide la desviación de la j-ésima observación de la i-ésima muestra de la correspondiente media del tratamiento. El término e_ij representa el error aleatorio y juega el mismo papel que los términos de error en los modelos de regresión. Una forma alternativa de esta misma ecuación y que se prefiere se obtiene al sustituir

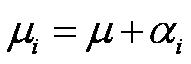
sujeta a la restricción 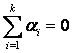, de aquí podemos escribir

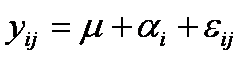
donde m es la media general de todas las observaciones es decir:

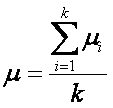
y a_i se denomina el efecto de i-ésimo tratamiento.

La hipótesis nula de que las k medias poblacionales son iguales contra la alternativa de que al menos de de las medias son diferentes se puede reemplazar ahora por la hipótesis equivalente,

H₀: a₁ = a₂ = _{.. .}= a_k = 0

H₁: al menos una es diferente de cero.

Nuestra prueba se basará en una comparación de dos estimaciones independientes de la varianza poblacional común s². Estas estimaciones se obtendrán al dividir la variabilidad total de nuestros datos, que se presentan en la doble sumatoria

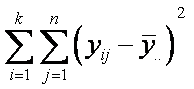
en dos componentes.

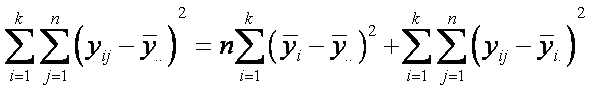
Esta ecuación es llamada la Identidad de la suma de cuadrados, ver [Walpole et all] para la prueba.

Será conveniente en lo que sigue identificar los términos de la identidad de suma de cuadrados mediante la siguiente notación.

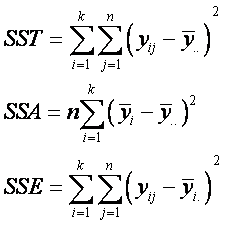
SST = suma total de cuadrados

SSA = suma de cuadrados de tratamiento

SSE =suma de cuadrados de error.

La identidad de la suma de cuadrados se puede presentar de manera simbólica con la ecuación.

SST = SSA + SSE.

Formulas para el cálculo de sumas de cuadrados.

A continuación presentamos un conjunto de formulas mas simples para calcular la suma de cuadrados (dejamos al lector su demostración).

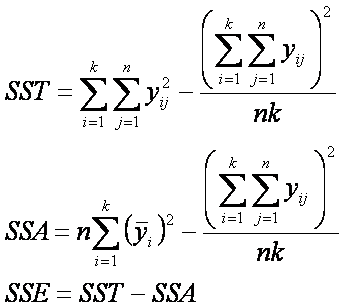
El valor esperado de SSA es:

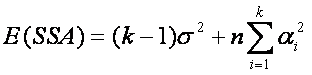
Si H₀ es verdadera, una estimación de s², que se basa en k-1 grados de libertad, la proporciona la expresión

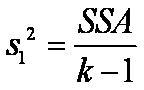
la cual se denomina cuadrado medio del tratamiento.

Un segundo e independiente estimados de s², que se basa en k(n-1) grados de libertad, es la formula ya familiar

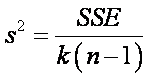
la cual se denomina cuadrado del error.

Cuando Ho es verdadero, la razón es un valor de la variable aleatoria F con k-1 y k(n-1) grados de libertad. Como sobrestima s² cuando H₀ es falsa, tenemos una prueba de una sola cola con la región crítica completamente en la cola derecha de la distribución.

La hipótesis nula H₀ se rechaza en el nivel de significancia a cuando

f >fa[k-1, k(n-1)]

Análisis de variancia para probar m1 = m2 = m3 = m4 = m5
Fuente de variación	Suma de cuadrados	Grados de libertad	Cuadrado medio	f calculada
Regresión	SSA	k-1	s1 =SSA/(k-1)	s1/s2
Error	SSE	k(n-1)	s2=SSE/ (k*(n-1))
Total	SST	nk-1
rechazamos H0, al nivel de significancia a cuando f > fa(k, n-(k+1))

Cálculo utilizando MINITAB

Para llevar a cabo el procedimiento utilizando MINITAB una vez introducidos los datos en la hoja de trabajo ir al menú Stat > ANOVA > One-Way… :

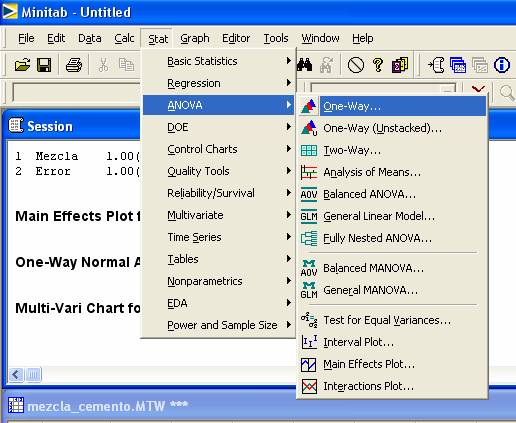
Después aparecerá la caja de diálogo

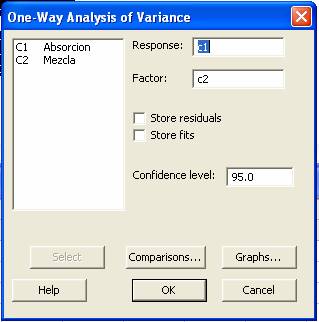
Ejemplo 10.

Para los datos de la Tabla 1, realizar el análisis de varianza.

y =

551 595 639 417 563

457 580 615 449 631

450 508 511 517 522

731 583 573 438 613

499 633 648 415 656

632 517 677 555 679

---------------------------------------------------------------------

Análisis de Varianza

---------------------------------------------------------------------

Fuente de Suma Grados de Cuadrado F calc

Variación cuadrados Libertad medio

---------------------------------------------------------------------

Regresión 85356.47 4 21339.12 4.30

Error 124020.33 25 4960.81

Total 209376.80 29

---------------------------------------------------------------------

Con (1-alfa) = 0.990 tenemos 4.30 > 4.18

Dada esta información rechazamos la hipótesis nula dado que F es mayor que el Fcalc.

El código en MATLAB para este ejemplo es:

function z = MiAnova(y)

n = length(y(:,1));

k = length(y(1,:));

Suma2 = 0;

Suma = 0;

for ren = 1:n

for col = 1:k

Suma2 = Suma2 + y(ren, col)^2;

Suma = Suma + y(ren, col);

end;

end;

SST = Suma2 - Suma^2/n/k;

SSA = n*sum(mean(y).^2) - Suma^2/n/k;

SSE = SST - SSA;

v1 = k-1;

v2 = k*(n-1);

s1 = SSA/v1;

s2 = SSE/v2;

F = s1/s2;

alfa = 0.01;

Fc = Finv(1-alfa, v1, v2);

fprintf('---------------------------------------------------------------------\n');

fprintf('Analisis de Varianza\n');

fprintf('---------------------------------------------------------------------\n');

fprintf('Fuente de Suma Grados de Cuadrado F calc\n');

fprintf('Variacion cuadrados Libertad medio \n');

fprintf('---------------------------------------------------------------------\n');

fprintf('Regresion %13.2f %13.f %13.2f %13.2f\n', SSA, v1, s1, F);

fprintf('Error %13.2f %13.f %13.2f \n', SSE, v2, s2);

fprintf('Total %13.2f %13.f \n', SST, v1+v2);

fprintf('---------------------------------------------------------------------\n');

fprintf('Con (1-alfa) = %5.3f tenemos %13.2f > %13.2f\n', 1-alfa, F, Fc);

z = F;

Esta implementación se puede realizar con el comando anova1 de MATLAB y para este ejemplo los resultados son:

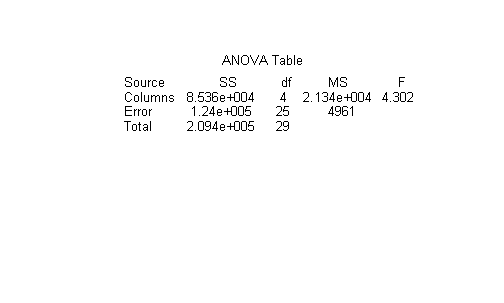
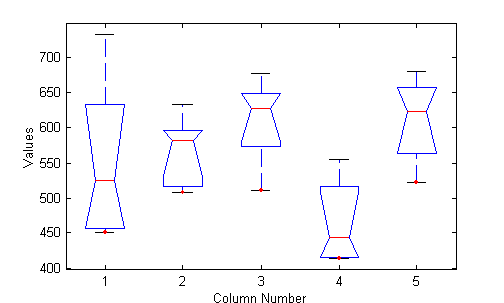
La solución utilizando MINITAB es

One-way ANOVA: Absorcion versus Mezcla

Source DF SS MS F P

Mezcla 4 85356 21339 4.30 0.009

Error 25 124020 4961

Total 29 209377

S = 70.43 R-Sq = 40.77% R-Sq(adj) = 31.29%

Individual 95% CIs For Mean Based on

Pooled StDev

Level N Mean StDev --+---------+---------+---------+-------

1 6 553.33 110.15 (-------*--------)

2 6 569.33 47.99 (-------*--------)

3 6 610.50 59.95 (-------*--------)

4 6 465.17 57.61 (-------*--------)

5 6 610.67 58.78 (-------*--------)

--+---------+---------+---------+-------

420 490 560 630

Pooled StDev = 70.43

Para el valor P podemos ver que es menor que el nivel de significancia por lo tal la hipótesis debe ser rechazada y tenemos medias diferentes.

Ejemplo 11.

Parte de un estudio que se llevo a cabo en el Instituto Politécnico y Universidad Estatal de Virginia, se diseño para medir los niveles de actividad de fosfatasa alcalina en suero de niños con crisis convulsivas que reciben terapia contra convulsiones bajo el cuidado de un médico particular. Se encontraron 45 sujetos para estudio y se clasificaron en cuatro grupos según el medicamento administrado:

G-1: Control (No reciben anticonvulsivos y no tienen historial de crisis convulsivas)

G-2: Fenobartibal.

G-3: Carbanacepina.

G-4: Otros anticonvulsivos.

Se determinó el nivel de actividad de la fosfatasa alcalina en suero a partir de muestras sanguíneas obtenidas de cada sujeto y se registraron en la siguiente tabla. Pruebe la hipótesis al nivel de significancia de 0.05 de que el nivel promedio de actividad de fosfatasa alcalina en suero es el mismo para los cuatro grupos.

Nivel de Actividad de fosfatasa alcalina en suero
G-1		G-2	G-3	G-4
49.20	97.50	97.07	62.10	110.60
44.54	105.00	73.40	94.95	57.10
45.80	58.05	68.50	142.50	117.60
95.84	86.60	91.85	53.00	77.71
30.10	58.35	106.60	175.00	150.00
36.50	72.80	0.57	79.50	82.90
82.30	116.70	0.79	29.50	115.50
87.85	45.15	0.77	78.40
105.00	70.35	0.81	127.50
95.22	77.40

La solución con MINITAB es

Results for: fosfatasa_suero.MTW

One-way ANOVA: Actividad versus Tratamiento

Source DF SS MS F P

Tratamiento 3 14136 4712 3.61 0.021

Error 41 53474 1304

Total 44 67609

S = 36.11 R-Sq = 20.91% R-Sq(adj) = 15.12%

Individual 95% CIs For Mean Based on

Pooled StDev

Level N Mean StDev --+---------+---------+---------+-------

1 20 73.01 25.75 (----*-----)

2 9 48.93 47.11 (-------*-------)

3 9 93.61 46.57 (-------*-------)

4 7 101.63 31.02 (--------*--------)

--+---------+---------+---------+-------

30 60 90 120

Pooled StDev = 36.11

En este caso el valor P es 0.021 así que para un grado de significancia del 5% este valor es inferior y la hipótesis de que las varianzas

4. Pruebas de igualdad de varianzas.

Aunque la razón f que se obtiene del procedimiento de análisis de varianza es insensible a desviaciones de la suposición de varianzas iguales para las k poblaciones normales cuando las muestras son de tamaño igual, aún podemos preferir tener precaución y realizar una prueba preliminar para la homogeneidad de varianzas. Tal prueba en realidad sería aconsejable en el caso de tamaños de muestras diferentes, donde si hay una duda razonable, con respecto a la homogeneidad de la varianzas poblacionales. Suponga, por tanto, que deseamos probar la hipótesis nula

H₀ :

H₁ : No todas las varianzas son iguales.

La prueba que utilizaremos, llamada prueba de Bartlett, se basa en una estadística cuya distribución muestral proporciona valores críticos exactos cuando los tamaños muéstrales son iguales. Estos valores críticos para tamaños iguales de muestras también se pueden utilizar para obtener aproximaciones altamente precisas de los valores críticos para tamaños diferentes de las muestras.

Los pasos para la prueba de Bartlett son:

Primero : Calculamos las k varianzas muestrales s²₁, s²₂, ..., s²_k a partir de las muestras de tamaño n₁, n₂, ... n_k, con .

Segundo : Combinamos las varianzas muestrales para obtener la estimación combinada.

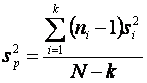
Ahora bien,

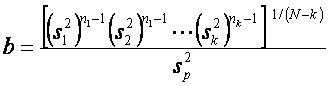
es un valor de una variable aleatoria B que tiene una distribución Bartlett. Para el caso especial donde n₁ = n₂ = ... = n_k = n, rechazamos H₀ en el nivel de significacancia a si

b <b_k(a,n)

donde b_k(a,n) es el valor crítico que deja un área de tamaño a en la cola izquierda de una distribución Bartlett. Cuando los tamaños son diferentes, la hipótesis nula se rechaza en el nivel de significancia a si

b <b_k(a,n₁, n₂, ..., n_k)

donde

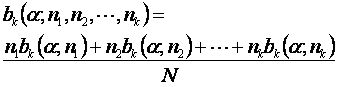
Ejemplo 12.

Utilice la prueba de Bartlett para probar la hipótesis, en el nivel de significancia 0.01, que las varianzas poblacionales de los cuatro grupos de medicamentos del ejemplo 11 son iguales.

Nuestra hipótesis a probar es:

H₀ :

H₁ : No todas las varianzas son iguales.

Para los datos dados tenemos que

n₁ = 20, n₂ = 9, n₃ = 9, n₄ = 7, N = 45 y k = 4;

Por lo tanto rechazamos cuando b < b₄(0.001, 20, 9, 9, 7)

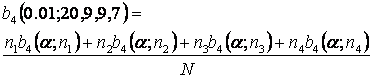
los valores de b_k(a,n_j), son extraídos de una tabla de valores críticos b

	valor
b(0.01,20)	0.8586
b(0.01,9)	0.6892
b(0.01,7)	0.6992

destituyendo valores tenemos:

b4(0.01; 20, 9, 9, 7) = (20*0.8586 + 9*0.6892 + 9*0.6892 + 7*0.6992)/45 = 0.7513

Las varianzas de cada grupo las calculamos

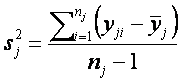
con lo cual obtenemos s² = [662.862, 2219.781, 2168.434, 946.032]

sp2 = [(662.862)*(19) + (2219.781)*(8) + (2168.434)*(8) + (946.032)*(6)]/41 = 1301.861

El estadístico b lo calculamos

b = [(662.862)¹⁹ (2219.781)⁸ (2168.434)⁸ (946.032)⁶]^1/4

^{---------------------------------------------------------------------------}

1301.861

b = 0.8557

La decisión es no rechazar la hipótesis y concluir que las varianzas poblacionales de los cuatro grupos de medicamentos no son significativamente diferentes.

5. Comparación de un solo grado de libertad.

El análisis de varianza es una clasificación unilateral, o experimento de un factor, como a menudo se llama, solamente indica si la hipótesis de media iguales se puede rechazar o no. Por lo general, un experimentador preferiría que su análisis realizara pruebas más profundas. Con relación al ejemplo 10 podemos, al rechazar la hipótesis nula, pero aun no sabemos donde existe diferencia entre las mezclas.

Prueba de Duncan.

Es un procedimiento utilizado para realizar la comparación de rangos múltiples de medias. Este procedimiento se basa en la noción general de un rango studentizado (recordar distribución t-student). El rango de cualquier subconjunto de p medias muestrales debe exceder cierto valor antes de que se encuentre que cualquiera de la p medias es diferentes. Este valor se llama rango de menor significancia para las p medias y se denota con R_p donde

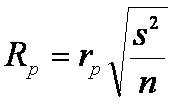
donde:

1. r_p son los rangos studentizado de menor significancia y depende del nivel de significancia y den número de grados de libertad.

2. s2 es el cuadrado medio del error y se toma de la tabla de análisis de varianza

3. n es el número de elementos para un tratamiento especifico.

4. p representa el tamaño del conjunto de medias.

5. y R_p puede entenderse como la diferencia mínima que debe existir entre la media mas grande y la más pequeña de un conjunto de tamaño p.

Los pasos que debemos seguir para aplicar la prueba de Duncan son:

1. Calcular el valor de cada una de las medias correspondientes a cada tratamiento y ordenarlas de mayor a menor, ya ordenadas las renumeraremos de 1 a p. Note que inicialmente p es igual al número de tratamientos k.

2. Determinar de una tabla los valores r_p para un valor de significancia a.

3. Calcular los Rp de acuerdo con la expresión anterior y tomar de la tabla de análisis de varianza el valor s2 = SSE/(k*(n-1))

4. Probar por rangos que vayan de la media 1 a la p

5. Si la hipótesis se cumple, es decir si R_p < m_i+p – m_i, terminamos

6. Hacemos rangos más pequeños p = p-1 y regresamos al paso 4 mientras p > 1.

Ejemplo 13.

Consideremos un ejemplo hipotético donde tenemos los siguientes valores para las medias de 6 tratamientos.

Paso 1.

media	m2	m5	m1	m3	m6	m4
y	14.5	16.75	19.84	21.12	22.90	23.20
n	5	5	5	5	5	5

Paso 2.

Los valores de r_p los obtenemos de tablas.

p	2	3	4	5	6
rp	2.919	3.066	3.160	3.226	3.276

Paso 3.

Calculamos los Rp para nuestro ejemplo, tomando el valor de s² = 2.45 del análisis de varianza

R²_p = r_p*[s²/n]^1/2

R²₂ = r₂*[s²/n]^1/2 = 2.919*[2.45/5]^1/2 = 2.043

R²₃ = r₃*[s²/n]^1/2 = 3.066*[2.45/5]^1/2 = 2.146

R²₄ = r₄*[s²/n]^1/2 = 3.160*[2.45/5]^1/2 = 2.212

R²₅ = r₅*[s²/n]^1/2 = 3.226*[2.45/5]^1/2 = 2.258

R²₆ = r₆*[s²/n]^1/2 = 3.276*[2.45/5]^1/2 = 2.293

En resumen

p	2	3	4	5	6
rp	2.919	3.066	3.160	3.226	3.276
Rp	2.043	2.146	2.212	2.258	2.293

Paso 4.

Comenzamos con p=6, por lo tanto R6 = 2.293 y probamos

m₄ – m₂ = 23.20 - 14.5 = 8.7

Paso 5.

m₄ – m₂ es mayor que 2.293, por lo tanto el rango no es 6.

Paso 6.

p = 5.

Paso 4.1

m₄ – m₅ = 23.20 – 16.75 = 6.45

m₆ – m₂ = 22.90 – 14.50 = 8.4

Paso 5.1

m₄ – m₅ es mayor que R₅ = 2.296, y

m₆ – m₂ es mayor que R₅ = 2.296, por lo tanto el rango no es 5.

Paso 6.1

p = 4.

Paso 4.2

m₄ – m₁ = 23.20 – 19.84 = 3.36

m₆ – m₅ = 22.90 – 16.75 = 6.15

m₃ – m₂ = 21.12 – 14.50 = 6.62

Paso 5.2

m₄ – m₁ es mayor que R₄ = 2.212,

m₆ – m₅ es mayor que R₄ = 2.212,

m₃ – m₂ es mayor que R₄ = 2.212, y por lo tanto el rango no es 4.

Paso 6.2

p = 3.

Paso 4.3

m₄ – m₃ = 23.20 – 21.12 = 2.08

m₆ – m₁ = 22.90 – 19.84 = 3.50

m₃ – m₅ = 21.12 – 16.75 = 4.37

m₁ – m₂ = 19.84 – 14.50 = 5.84

Paso 5.3

m₄ – m₃ es menor que R₃ = 2.146, por tanto hay un rango 3 dado por [m₄, m₆, m₃].

Para el resto

m₆ – m₁ es mayor que R₃ = 2.146,

m₃ – m₅ es mayor que R₃ = 2.146,

m₁ – m² es mayor que R₃ = 2.146 y por lo tanto el rango no es 3.

Paso 6.3

p = 2.

Paso 4.4

Como ya determinamos el conjunto [m₄, m₆, m₃], trabajamos con el resto de las medias así

m₃ – m₁ = 21.12 - 19.84 = 2.08

m₁ – m₅ = 19.84 - 16.75 = 3.09

m₅ – m₂ = 16.75 - 14.50 = 2.25

Paso 5.4

m₃ – m₁ es menor que R₂ = 2.043, por tanto hay un rango 2 dado por [m₃ – m₁ ].

Para las demás

m₁ – m₅ es mayor que R₂ = 2.043,

m₅ – m₂ es mayor que R₂ = 2.043 por lo tanto el rango no es 2.

Paso 6.3

p = 1. Terminamos.

Finalmente los rangos quedan

m = {[m₄, m₆, m₃, m₁], [m₅], [m₂]}

Regresar.