Diseño de bloques completos aleatorizados.

El ejemplo clásico, que utiliza un diseño de bloques aleatorizado, es un experimento agrícola en el que se comparan diferentes fertilizantes según su capacidad de aumentar el rendimiento de una cosecha en particular. En lugar de asignar los fertilizantes al azar a muchas parcelas en un área grande de composición de suelos variable, se deben asignar los fertilizantes a bloques más pequeños compuestos de parcelas homogéneas. La variación entre estos bloques, que es probablemente más significativa comparada con la uniformidad de las parcelas dentro de un bloque, elimina el error experimental en el análisis de varianza.

Una disposición típica para el diseño de bloques completos aleatorizados con el uso de tres mediciones en cuatro bloques es el siguiente.

bloque 1	bloque 2	bloque 3	bloque 4
t2	t1	t3	t2
t1	t3	t2	t1
t3	t2	t1	t3

Las t denotan la asignación a los bloques de cada uno de los tres tratamientos. Por supuesto, la asignación real de los tratamientos a unidades dentro de los bloques se realiza al azar. Una vez que el experimento termina, los datos se pueden registrar como en el siguiente arreglo de 3x4:

Tratamiento	Bloques:	1	2	3	4
1		y11	y12	y13	y14
2		y21	y22	y23	y24
3		y31	y32	y33	y34

donde y_ij representa la respuesta que se obtiene al utilizar el i-ésimo tratamiento en el j-ésimo bloque.

Generalicemos y consideremos el caso de k tratamientos que se asignan a b bloques. Los datos se pueden resumir como se muestra en el arreglo rectangular de kxb de la siguiente tabla

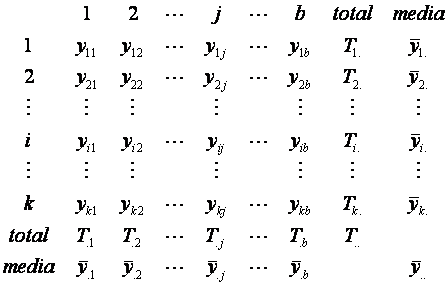
Se supondrá que las variables y_ij i=1,2,...,k y j = 1,2,...,b, son valores de variables independientes que tienen distribuciones normales con media m_ij y varianza común s². Definimos

Ti. = suma de las observaciones para el i-ésimo tratamiento.

T.j = suma de las observaciones para el j-ésimo bloque.

T.. = suma de todas las bk observaciones.

= media de las observaciones para el i-ésimo tratamiento

= suma de las observaciones para el j-ésimo bloque.

= suma de todas las bk observaciones.

Representamos como m_i. el promedio de las b medias poblacionales para el i-ésimo tratamiento. Es decir,

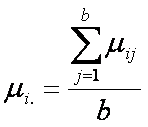
De manera similar, el promedio de las medias poblacionales para el j-ésimo bloque, se define como

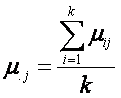
y el promedio de las b_k medias, m se define como

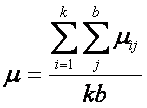
Para determinar si parte de la variación en nuestras observaciones se debe a diferencias entre los tratamientos, consideremos las pruebas.

H₀ : m₁ = m₂ = m₃ = m₄ = m₅

H₁ : al menos dos de las medias no son iguales.

Cada observación se puede escribir de la forma

donde e_ij mide la desviación del valor observado yij de la media poblacional m_ij. La forma de esta ecuación que se prefiere se obtiene al sustituir

donde a_i es, el efecto del i-ésimo tratamiento y b_j es el efecto del j-ésimo bloque. Se supone que los efectos del tratamiento y del bloque se pueden sumar. De aquí, podemos escribir

Nótese que el modelo parece el de la clasificación unilateral, la diferencia esencial es la introducción del efecto de bloque b_j. El concepto básico es muy semejante al de la clasificación unilateral excepto que debemos tomar en cuenta en el análisis el efecto adicional debido a los bloques, pues ahora controlamos de manera sistemática la variación en dos direcciones. Si imponemos ahora las restricciones

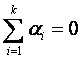y

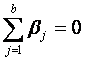
Entonces

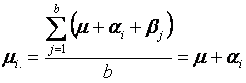
y

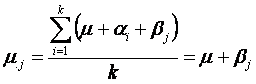
La hipótesis nula de que las k medias de tratamiento m_i. son iguales, y por tanto iguales a m, es equivalente ahora a probar la hipótesis

H₀ : a₁ = a₂ = _{.. .}= a_k = 0

H₁ : al menos una es diferente de cero.

Cada una de las pruebas de tratamiento se basará en una comparación de estimaciones independientes de la varianza poblacional común s². Estas estimaciones se obtendrán al dividir la suma total de cuadrados de nuestros datos en tres componentes por medio de la siguiente identidad.

Identidad de suma de cuadrados.

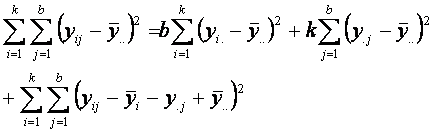
La identidad de suma de cuadrados se puede representar de manera simbólica con la ecuación

SST = SSA + SSB + SSE

donde:

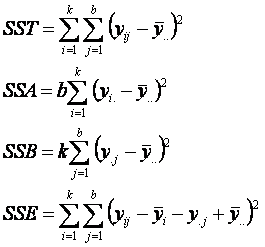
Podemos mostrar que los valores esperados de las sumas de cuadrados de tratamiento, bloque y error están dados por

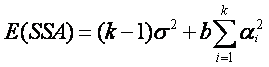
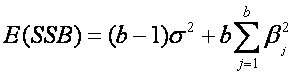
Si los efectos de tratamiento a₁ = a₂ = ... = a_k = 0, s₁² es un estimador insesgado de s² y podemos calcular la varianza como

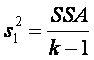
Por bloques tenemos el mismo caso si b₁ = b₂ = ... = b_b = 0 s₂² también un estimador insesgado de s² y podemos calcular la varianza como

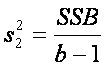
Una tercera estimación de s², basada en (k-1)(b-1) grados de libertad e independiente de s₁² y s₂² es

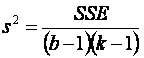
Para probar la hipótesis nula de que los efectos de tratamiento son todos iguales a cero, calculamos la razón

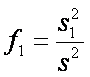
que es un valor de la variable aleatoria F₁ que tiene una distribución F con k-1 y (k-1)(b-1) grados de libertad. La hipótesis nula H₀ se rechaza en el nivel de significancia a cuando

f₁ >fa[k-1, (k-1)(b-1)]

Análisis de variancia para probar m1 = m2 = m3 = m4 = m5
Fuente de variación	Suma de cuadrados	Grados de libertad	Cuadrado medio	f calculada
Tratamientos	SSA	k-1	s1^2 =SSA/(k-1)	s1/s
Bloques	SSB	b-1	s2^2 =SSB/(b-1)	s2/s
Error	SSE	(k-1)(b-1)	s^2=SSE/ (k-1)(b-1)
Total	SST	bk-1
rechazamos H0, al nivel de significancia a cuando f1 >fa[k-1, (k-1)(b-1)]

Uso de MINITAB

Para llevar a cabo estas pruebas de hipótesis en MINITAB, una vez introducidos los datos ir al menú Stat > ANOVA > Two-Way ..

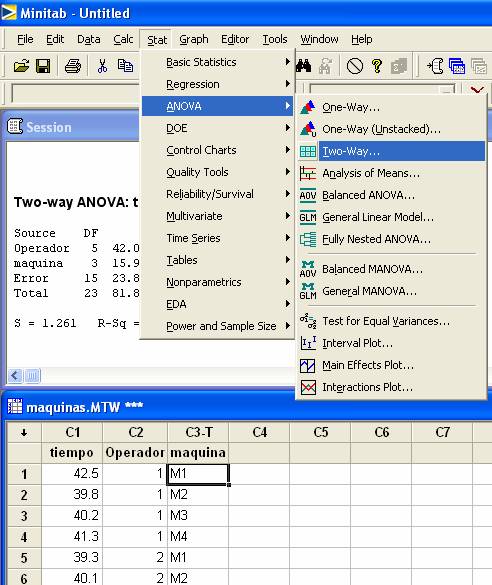
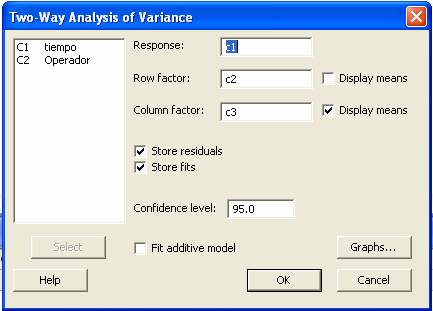
En la caja de diálogo introducir la respuesta y los factores por renglón y por columna.

Ejemplo 1

Se consideran cuatro diferentes máquinas M1, M2, M3 y M4 para el ensamblaje de un producto particular. Se decide que utilizar seis operadores diferentes en un experimento de bloques aleatorizados para comparar las máquinas. Las máquinas se asignan en orden aletorio a cada operador. La operación de las máquinas requiere destreza física y se anticipa que habrá una diferencia entre los operadores en la rapidez con la que operan las máquinas. Se registra la cantidad de tiempo en segundos para ensamblar el producto

Maquina	operador	1	2	3	4	5	6	TOTAL
1		42.5	39.3	39.6	39.9	42.9	43.6	247.8
2		39.8	40.1	40.5	42.3	42.5	43.1	248.3
3		40.2	40.5	41.3	43.4	44.9	45.1	255.4
4		41.3	42.2	43.5	44.2	45.9	42.3	259.4
total		163.8	162.1	164.9	169.8	176.2	174.1	1010.9

Pruebe la hipótesis nula.

Del análisis de los valores P tenemos que este es igual a 0.048, por lo tanto, para un nivel de significacancia del 0.05 tenemos que el valor P es más pequeño, por lo cual la hipótesis debe ser rechazada y no existe evidencia de que las máquinas trabajen a la misma velocidad.

Results for: maquinas.MTW

Two-way ANOVA: tiempo versus Operador, maquina

Source DF SS MS F P

Operador 5 42.0871 8.41742 5.29 0.005

maquina 3 15.9246 5.30819 3.34 0.048

Error 15 23.8479 1.58986

Total 23 81.8596

S = 1.261 R-Sq = 70.87% R-Sq(adj) = 55.33%

Two-way ANOVA: tiempo versus Operador, maquina

Source DF SS MS F P

Operador 5 42.0871 8.41742 5.29 0.005

maquina 3 15.9246 5.30819 3.34 0.048

Error 15 23.8479 1.58986

Total 23 81.8596

S = 1.261 R-Sq = 70.87% R-Sq(adj) = 55.33%

Individual 95% CIs For Mean Based on

Pooled StDev

Operador Mean -----+---------+---------+---------+----

1 40.950 (-------*-------)

2 40.525 (-------*--------)

3 41.225 (--------*-------)

4 42.450 (-------*--------)

5 44.050 (-------*--------)

6 43.525 (-------*-------)

-----+---------+---------+---------+----

40.0 41.6 43.2 44.8

Individual 95% CIs For Mean Based on

Pooled StDev

maquina Mean -----+---------+---------+---------+----

M1 41.3000 (--------*--------)

M2 41.3833 (--------*--------)

M3 42.5667 (--------*--------)

M4 43.2333 (--------*--------)

-----+---------+---------+---------+----

40.8 42.0 43.2 44.4

Ejemplo 2

Se utilizaron cuatro clases de fertilizantes f1, f2, f3 y f4 para estudiar el rendimiento en el cultivo de fríjol. El suelo de dividió en tres bloques, cada uno de los cuales contiene 4 parcelas homogéneas. A continuación se presentan los rendimientos en kilogramos por parcela, así como los tratamientos correspondientes:

Bloque 1 Bloque 2 Bloque 3

f1 = 42.7 f3 = 50.9 f4 = 51.1

f3 = 48.5 f1 = 50.0 f2 = 46.3

f4 = 32.8 f2 = 38.0 f1 = 51.9

f2 = 39.3 f4 = 40.2 f3 = 53.5

a) Realice un análisis de varianza con un nivel de significacancia de 0.05, y utilice el modelo de bloques aleatorios por completo

Del análisis de varianza podemos ver que con un nivel de significancia de 0.05 que el valor P es 0.030. Esto significa que la hipótesis debe ser rechazada y no hay evidencia de que los rendimientos de fríjol sean iguales.

Results for: fertilizante.MTW

Two-way ANOVA: Rendimiento versus Fertilizante, Bloque

Source DF SS MS F P

Fertilizante 3 218.193 72.7311 6.11 0.030

Bloque 2 197.632 98.8158 8.30 0.019

Error 6 71.402 11.9003

Total 11 487.227

S = 3.450 R-Sq = 85.35% R-Sq(adj) = 73.13%

Individual 95% CIs For Mean Based on

Pooled StDev

Fertilizante Mean -------+---------+---------+---------+--

f1 48.2000 (--------*---------)

f2 41.2000 (--------*---------)

f3 50.9667 (---------*---------)

f4 41.3667 (---------*--------)

-------+---------+---------+---------+--

40.0 45.0 50.0 55.0

Individual 95% CIs For Mean Based on

Pooled StDev

Bloque Mean -------+---------+---------+---------+--

b1 40.825 (--------*-------)

b2 44.775 (--------*-------)

b3 50.700 (-------*--------)

-------+---------+---------+---------+--

40.0 45.0 50.0 55.0

Que es un residuo para un diseño de Bloques completamente aleatorio

La formulación de bloques completamente aleatorios es otra situación experimental en la cual la gráfica hace que el analista se sienta cómodo con una “imagen ideal” o con la detección de dificultades. Hay que recordar que el modelo para bloques completamente aleatorios es

Con las restricciones impuestas

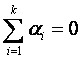y

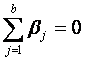
Para determinar qué es lo que en realidad constituye un residuo, considere que

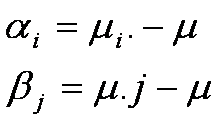
Como resultado, el valor ajustado o pronóstico esta dado por

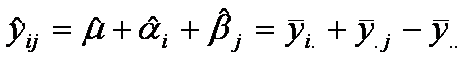
y, entonces, el residuo de observación (i,j) está dado por

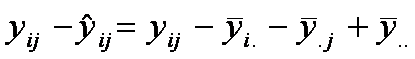
Observe que , el valor ajustad es un estimador de la media m_ij. Esto es consistente con la partición de la variabilidad en la que la suma de los errores al cuadrado es

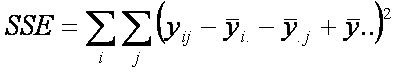
Las técnicas visuales en la formación de bloques completamente aleatorios implican graficar los residuos por separado para cada tratamiento y bloque. Si la suposición de varianza homogénea se cumple, el analista debería esperar una variabilidad aproximadamente igual.

Ejemplo 3

Para los datos del ejemplo 1 tenemos:

Maquina	operador	1	2	3	4	5	6	TOTAL
1		42.5	39.3	39.6	39.9	42.9	43.6	247.8
2		39.8	40.1	40.5	42.3	42.5	43.1	248.3
3		40.2	40.5	41.3	43.4	44.9	45.1	255.4
4		41.3	42.2	43.5	44.2	45.9	42.3	259.4
total		163.8	162.1	164.9	169.8	176.2	174.1	1010.9

Para llevar a cabo las gráficas de residuos en MINITAB hacer

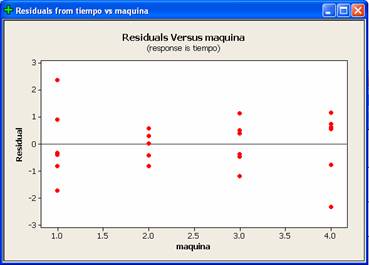
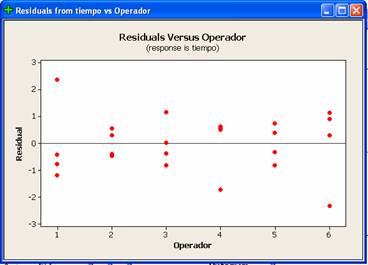
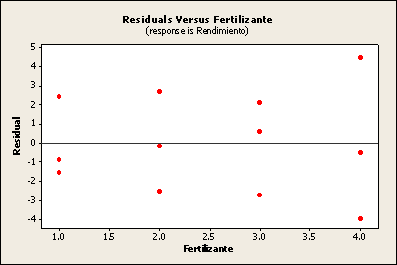
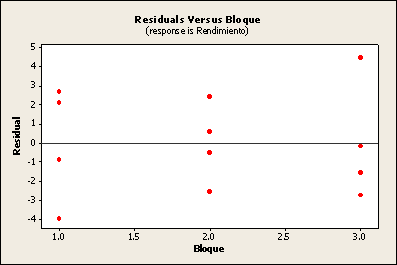
Las siguientes figuras muestran las gráficas de residuos para tratamientos separados y bloques separados. La figura de la izquierda revela que la varianza no podría ser la misma para todas las máquinas. Lo mismo sería valido para la varianza del error de cada uno de los seis operadores. Sin embargo son dos residuos inusualmente grandes los que parecen producir la dificultad.

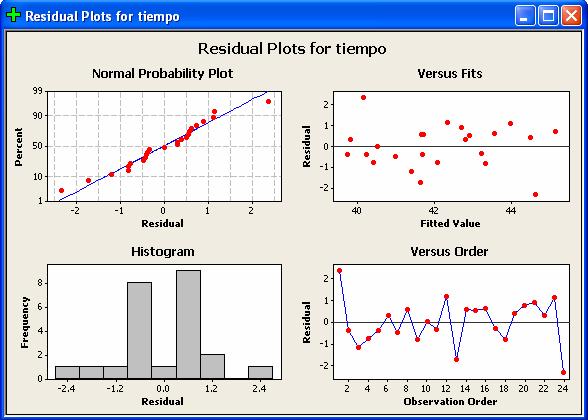
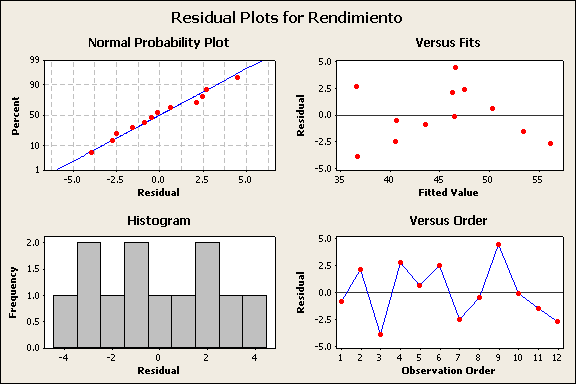
La siguiente figura, una gráfica de residuos, dan evidencia razonable de un comportamiento aleatorio donde sobresalen dos residuos grandes.

Ejemplo 4

Para los datos del ejemplo 2 hacer el análisis de los residuos.

Bloque 1 Bloque 2 Bloque 3

f1 = 42.7 f3 = 50.9 f4 = 51.1

f3 = 48.5 f1 = 50.0 f2 = 46.3

f4 = 32.8 f2 = 38.0 f1 = 51.9

f2 = 39.3 f4 = 40.2 f3 = 53.5

Bibliografía.

[Walpole et all] Walpole Ronald E., Myers Raymond H., Myers Sharon L. y Ye Keying “Probabilidad y estadística para Ingeniería y ciencias”. Octava Edición. Pearson Education. 2007.

Regresar.