Experimentos factoriales

Considere una situación en la que haya interés por estudiar el efecto de dos factores A y B, sobre alguna respuesta. Por ejemplo, en un experimento químico nos gustaría variar en forma simultánea la presión de reacción y el tiempo de reacción, y estudiar el efecto de cada uno sobre el producto. En un experimento biológico resulta de interés estudiar el efecto que tienen el tiempo de secado sobre la cantidad de sólidos (porcentaje en peso) que queda en las muestras de levadura. El término factor se utiliza en un sentido general para denotar cualquier característica del experimento que pueda variar de un ensayo a otro, como la temperatura, el tiempo de presión. Los niveles de un factor se definen como los valores reales que se utilizan en el experimento.

Para cada uno de estos casos, es importante determinar no sólo si cada uno de los factores tiene influencia en la respuesta, sino también si hay interacción significativa entre ellos.

Ejemplo 5.1

Considere los datos siguientes de temperatura (factor A con niveles t1 t2 y t3 en orden creciente) y tiempo de secado (d1. d2 y d3 también en orden creciente). La respuesta se expresa en porcentaje de sólidos. Estos datos son hipotéticos por completo.

B

A	d1	d2	d3	Total
t1	4.4	8.8	5.2	18.4
t2	7.5	8.5	2.4	18.4
t3	9.7	7.9	0.8	18.4
Total	21.6	25.2	8.4	55.2

Interacción en el experimento de dos factores

En el modelo de bloques aleatorizados que se estudió en forma previa, se supuso que en cada bloque se tomaba una observación de cada tratamiento. Si la suposición del modelo es correcta, es decir, si los bloques y los tratamientos son los únicos efectos reales y la interacción no existe, el valor esperado del error cuadrático de la media es la varianza, s², del error experimental. Sin embargo, suponga que existe interacción entre los tratamientos y los bloques, como se indica en el modelo

Representación Gráfica de la Interacción

La presencia de interacción, así como su influencia científica, puede interpretarse bien usando gráficas de interacción. Estas dan con claridad una visión panorámica de la tendencia de los datos para mostrar el efecto que tiene cambiar un factor conforme se pasa de un nivel a otro del segundo factor.

Para mostrar la gráfica en MINITAB dar

Graph > Line Plot

Entonces aparecerá el menú

y al presionar ok aparecerá

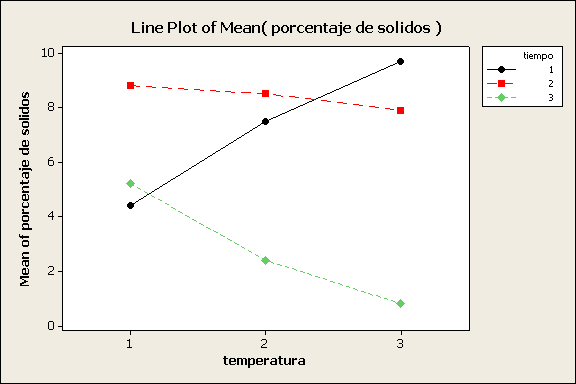
La siguiente figura ilustra la interacción marcada entre la temperatura y el tiempo de secado. La interacción se revela en la falta de paralelismo entre las líneas. Debe ser claro que el paralelismo en las gráficas indica ausencia de interacción.

Análisis de varianza de dos factores

Para presentar las formulas generales para el análisis de varianza de un experimento de dos factores que utiliza observaciones repetidas en un diseño por completo aleatorio, debe considerarse el caso de n repeticiones de las combinaciones del tratamiento, determinadas por a niveles de factor A y b niveles del factor B. Las observaciones pueden calificarse usando un arreglo rectangular, donde los renglones representan los niveles del factor A; y las columnas, los del factor B. Cada combinación del tratamiento define una celda del arreglo. Así, se tiene ab celdas, cada una de las cuales contiene n observaciones. Se denota con y_ijk la k-esima observación tomada en el i-esimo nivel del factor A y j-esimo nivel del factor B;

	B
A	1	2	b	Total	Media
1	y111	y121	y1b1	Y1..	y1..
	y112	y122	y1b2
	y11n	y12n	y1bn
2	y211	y221	y2b1	Y2..	y2..
	y212	y222	y2b2
	y21n	y22n	y2bn
a	ya11	ya21	yab1	Ya..	ya..
	ya12	ya22	yab2
	ya1n	ya2n	yabn	Y…
Total	Y.1.	Y.2.	Y.b.
Media	y.1.	y.b.	y.b.		y…

Las observaciones en la celta ij-esimas constituyen una muestra aleatoria de tamaño n de una población que se supone tiene distribución normal con media m_ij y varianza s². Se supone que todas las ab poblaciones tienen la misma varianza s²

Se definen los símbolos siguientes, que son de utilidad

Y_ij. = suma de las observaciones en la (ij)-esima celda

Y_i.. = suma de las observaciones para el i-esimo nivel del factor A

Y_.j. = suma de las observaciones para el j-esimo nivel del factor B

Y… = suma de las abn observaciones,

= media de las observaciones en la (ij)-ésima celda

= media de las observaciones para el i-esimo nivel del factor A

= media de las observaciones para el j-esimo nivel del factor B

= media de todas las abn observaciones

A diferencia de la situación para un solo factor, esta vez supondremos que las poblaciones de las que se toman n observaciones independientes con distribución idénticas son combinación de los factores. Así mismo, se supondrá siempre que de cada combinación de factores se toma un número igual n de observaciones. En los casos en que los tamaños de las muestras por combinación son desiguales, los cálculos son más complicados, aunque los conceptos son transferibles.

Modelo e hipótesis para el problema con dos factores.

Cada observación puede escribirse en la siguiente forma

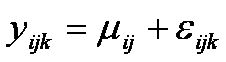
donde el termino e_ijk mide las observaciones, con respecto de la media m_ij, de los valores y_ijk observados en la (ij)-ésima celda. Si (ab)_ij denota el efecto de la interacción del i-ésimo nivel del factor A con el j-esimo nivel del factor B, a_i el efecto del i-ésimo nivel del factor A, b_j del j-ésimo factor B y m la media conjunta, escribimos

y entonces

a las que se imponen las restricciones

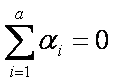
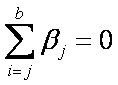
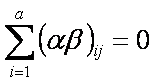
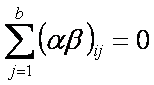
Las tres hipótesis por probar son las siguientes:

1.- Ho’: a₁ = a₂ = … = a_a = 0

H1’: Al menos una de las a_i no es igual a cero

2.- Ho’’: b₁ = b₂ = … = b_b = 0

H1’’: Al menos una de las b_j no es igual a cero

3.- Ho’’’: (ab)₁₁ = (ab)₁₂ = … = (ab)_ab = 0

H1’’’: Al menos una de las (ab)_ij no es igual a cero

La tabla para análisis de varianza para el experimento de dos factores con n repeticiones

Fuente de Variacion	Suma de Cuadrados	Grados de Libertad	Media Cuadrática	f calculada
Efecto principal
A	SSA	a-1	s1^2=SSA/(a-1)	f1=s1^2/s^2
B	SSB	b-1	s2^2=SSB/(b-1)	f2 = s2^2/s^2
Interacción
AB	SS(AB)	(a-1)(b-1)	S3^2=SS(AB)/(a-1)(b-1)	f3 = s2^3/s^2
Error	SSE	ab(n-1)	s^2=SSE/ab(n-1)
Total	SST	abn-1

La Hipótesis Ho’ se rechaza cuando f1 > f_a[a-1, ab(n-1)]

La Hipótesis Ho’’ se rechaza cuando f2 > f_a[b-1, ab(n-1)]

Concluimos Ho’’’ es verdadera o que hay interacción cuando f3 > f_a[(a-1), (b-1), ab(n-1)]

Desarrollo en MINITAB

Ir a la opción Stat > ANOVA > Balanced ANOVA

Donde aparecerá el cuadro de dialogo

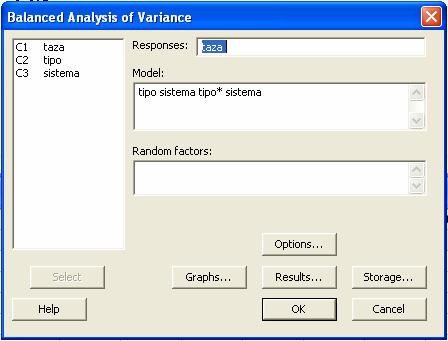
Ejemplo 5.2

En un experimento que se realizo para determinar cuál de los tres sistemas de misiles distintos es preferible, se midió la taza de combustión del propulsor para 24 arranques estáticos. Se emplearon 4 tipos de combustible diferentes. El experimento generó observaciones duplicadas de las tasas de combustión con cada combinación de los tratamientos.

Los datos ya codificados, se dan en la siguiente tabla. Pruebe las siguientes hipótesis: a) Ho’: no hay diferencia en las tasas medias de combustión cuando el propulsor se emplean diferentes sistemas de misiles, b) Ho’’: no existe diferencia en las tasas medias de combustión cuando de los cuatro tipos de propulsor, c) Ho’’’: no hay interacción entre los distintos sistemas de misiles y los tipos diferentes de propulsor.

Sistema de	Tipo de propulsor
misiles	b1	B2	b3	b4
a1	34.0	30.1	29.8	29.0
	32.7	32.8	26.7	28.9
a2	32.0	30.2	28.7	27.6
	33.2	29.8	28.1	27.8
a3	28.4	27.3	29.7	28.8
	29.3	28.9	27.3	29.1

Respuestas

ANOVA: taza versus tipo, sistema

Factor Type Levels Values

tipo fixed 4 1, 2, 3, 4

sistema fixed 3 1, 2, 3

Analysis of Variance for taza

Source DF SS MS F P

tipo 3 40.082 13.361 10.75 0.001

sistema 2 14.523 7.262 5.84 0.017

tipo*sistema 6 22.163 3.694 2.97 0.051

Error 12 14.910 1.242

Total 23 91.678

S = 1.11467 R-Sq = 83.74% R-Sq(adj) = 68.83%

ANOVA: taza versus tipo, sistema

Factor Type Levels Values

tipo fixed 4 1, 2, 3, 4

sistema fixed 3 1, 2, 3

Analysis of Variance for taza

Source DF SS MS F P

tipo 3 40.082 13.361 10.75 0.001

sistema 2 14.523 7.262 5.84 0.017

tipo*sistema 6 22.163 3.694 2.97 0.051

Error 12 14.910 1.242

Total 23 91.678

S = 1.11467 R-Sq = 83.74% R-Sq(adj) = 68.83%

a) Rechace Ho’ y concluya que los distintos sistemas de misiles generan tasas medias diferentes de combustión de propulsor. El valor P es aproximadamente 0.017.

b) Rechace Ho’’ y concluya que las tasas medias de combustión del propulsor no son las mismas para los cuatro tipos de propulsor. El valor P es mas pequeño que 0.0010

c) La interacción es casi insignificante al nivel 0.05, pero el valor P de aproximadamente 0.0512 indicaría que la interacción debe tomarse en cuenta.

Dada la conclusión dada en el inciso (c) verifiquemos gráficamente esta condición de dependencia.

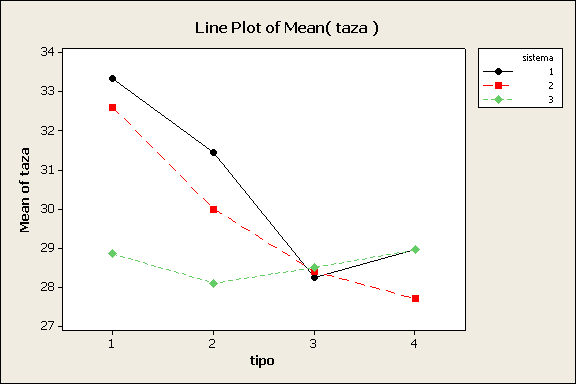
En la gráfica podemos ver claramente una falta total de paralelismo lo cual corrobora el resultado. Hay dependencia entre los dos factores de nuestro experimento que son el tipo de propulsor y el sistema de combustible

Ejemplo 5.3

Se realizo un experimento para estudiar el efecto de la temperatura y el tipo de horno sobre la vida de un componente en particular que está a prueba. En el experimento se utilizaron 4 tipos de horno y tres niveles de temperatura. Se asignaron cuatro piezas al azar, 2 para cada combinación de tratamientos, y se registraron los resultados siguientes

horno	temperatura	vida
1	500	227
1	500	221
1	550	187
1	550	208
1	600	174
1	600	202
2	500	214
2	500	259
2	550	181
2	550	179
2	600	198
2	600	194
3	500	225
3	500	236
3	550	232
3	550	198
3	600	178
3	600	213
4	500	260
4	500	229
4	550	246
4	550	273
4	600	206
4	600	219

Con un nivel de significancia de 0.05, pruebe las hipótesis de que:

a) las temperaturas diferentes no tienen efecto sobre la vida del componente;

b) los hornos distintos no tienen efecto en la vida del componente;

c) el tipo de horno y la temperatura no interactúan.

Results for: Hornos.MTW

ANOVA: vida versus horno, temperatura

Factor Type Levels Values

horno fixed 4 1, 2, 3, 4

temperatura fixed 3 500, 550, 600

Analysis of Variance for vida

Source DF SS MS F P

horno 3 4963.1 1654.4 5.18 0.016

temperatura 2 5194.1 2597.0 8.13 0.006

horno*temperatura 6 3126.2 521.0 1.63 0.222

Error 12 3833.5 319.5

Total 23 17117.0

S = 17.8734 R-Sq = 77.60% R-Sq(adj) = 57.07%

Conclusiones

a) Rechazamos la hipótesis dado que P=0.06 y concluimos que la temperatura influye en la vida del componente

b) Rechazamos la hipótesis dado que P=0.016 y concluimos que los diferentes tipos de horno influyen en la vida del componente

c) Aceptamos la hipótesis y por lo tanto existe interacción entre el tipo de horno y la temperatura. Gráficamente podemos ver

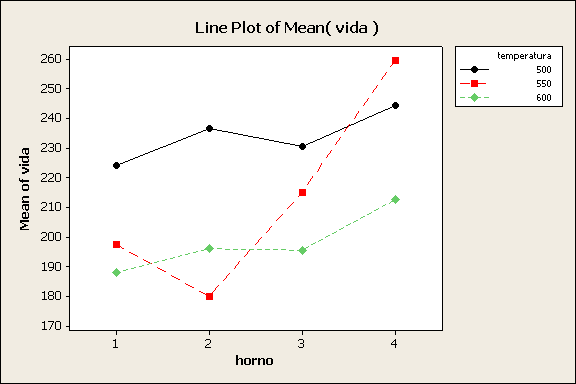
Ejemplo 5.4

Para determinar cuáles músculos necesitan sujetarse a un programa de acondicionamiento para mejorar el rendimiento individual en el servicio tendido que se usa en el tenis, el Departamento de salud, Educación Física y Recreación del Instituto Politécnico y Universidad Estatal de Virginia realizó un estudio de cinco músculos diferentes:

1 deltoides anterior

2 pectoral mayor

3 deltoides posterior

4 deltoides medio

5 tríceps

los cuales se probaron en 3 sujetos, y el experimento se efectuó 3 veces para cada combinación de tratamiento. Los datos electromiográficos se registraron durante el servicio y se presentan a continuación. Use un nivel de 0.01 de significancia para probar la hipótesis de que

a) diferentes sujetos tienen mediciones iguales del electromiograma

b) músculos diferentes no tienen efecto en las mediciones del electromiograma

c) los sujetos y los tipos de músculo no interactúan

ANOVA: entrenamiento versus musculo, sujeto

Factor Type Levels Values

musculo fixed 5 1, 2, 3, 4, 5

sujeto fixed 3 1, 2, 3

Analysis of Variance for entrenamiento

Source DF SS MS F P

musculo 4 7543.9 1886.0 26.95 0.000

sujeto 2 4814.7 2407.4 34.40 0.000

musculo*sujeto 8 11362.2 1420.3 20.30 0.000

Error 30 2099.2 70.0

Total 44 25820.0

S = 8.36494 R-Sq = 91.87% R-Sq(adj) = 88.08%

a) Rechazamos la hipótesis dado que P = 0 y concluimos que tenemos que diferentes sujetos tienen mediciones diferentes del electromiograma

b) Rechazamos la hipótesis dado que P = 0 y decimos que tienen efecto en las mediciones del electromiograma

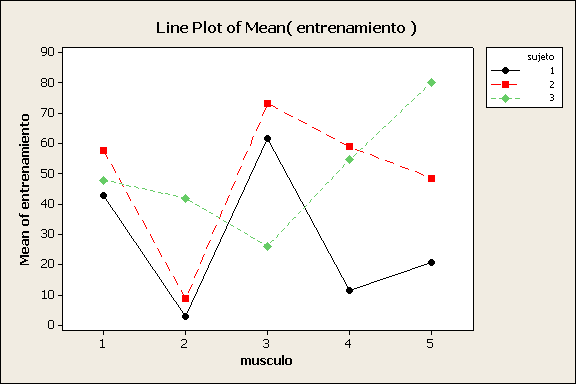
c) Rechazamos la hipótesis dado que P = 0 y concluimos que los sujetos y los tipos de músculo no interactúan. En la siguiente gráfica se ve un poco débil esta consideración aunque entre los sujetos 1 y 2 si hay mucho paralelismo.

Experimentos con tres factores

Ahora consideraremos experimentos en los cuales se tienen tres factores A, B y C. La formulación en muy similar, salvo que el número de combinaciones en el modelo crece. La siguiente es una tabla de ANOVA para el caso de experimentos con tres factores.

Fuente de Variacion	Suma de Cuadrados	Grados de Libertad	Media Cuadrática	f calculada
Efecto principal
A	SSA	a-1	s1^2=SSA/(a-1)	f1=s1^2/s^2
B	SSB	b-1	s2^2=SSB/(b-1)	f2 = s2^2/s^2
C	SSC	c-1	s3^2=SSB/(b-1)	f3 = s3^2/s^2
Interacción dos factores
AB	SS(AB)	(a-1)(b-1)	s4^2=SS(AB)/(a-1)(b-1)	f4 = s4^3/s^2
AC	SS(AC)	(a-1)(c-1)	s5^2=SS(AC)/(a-1)(c-1)	f5 = s5^3/s^2
BC	SS(BC)	(b-1)(c-1)	s6^2=SS(BC)/(b-1)(c-1)	f6 = s6^3/s^2
Interaccion tres factores
AB	SS(ABC)	(a-1)(b-1)(c-1)	s4^2=SS(AB)/(a-1)(b-1)(c-1)	f7 = s7^3/s^2
Error	SSE	abc(n-1)	s^2=SSE/abc(n-1)
Total	SST	abn-1

Ejemplo 5.5

En la producción de un material en particular hay tres variables de interés A, el efecto del operador (tres operadores): B el catalizador utilizando en el experimento (tres catalizadores); y C, el tiempo de lavado del producto después del proceso de enfriamiento (15 y 20 minutos). Con cada combinación de factores se hicieron tres corridas. Se pensaba que deberían estudiarse todas las interacciones entre los factores. Realice un análisis de varianza para probar los efectos que son significativos.

		Tiempo de lavado C
	15 Minutos			20 minutos
	B (Catalizador)			B (Catalizador)
A (Operador)	1	2	3	1	2	3
1	10.70	10.30	11.20	10.90	10.50	12.20
	10.80	10.20	11.60	12.10	11.10	11.70
	11.30	10.50	12.00	11.50	10.30	11.00
2	11.40	10.20	10.70	9.80	12.60	10.80
	11.80	10.90	10.50	11.30	7.50	10.20
	11.50	10.50	10.20	10.90	9.90	11.50
3	13.60	12.00	11.10	10.70	10.20	11.90
	14.10	11.60	11.00	11.70	11.50	11.60
	14.50	11.50	11.50	12.70	10.90	12.20

Los resultados del análisis de varianza utilizando MINITAB son

Results for: Material3F.MTW

ANOVA: Material versus Operador, Catalizador, Tiempo

Factor Type Levels Values

Operador fixed 3 1, 2, 3

Catalizador fixed 3 1, 2, 3

Tiempo fixed 2 15, 30

Analysis of Variance for Material

Source DF SS MS F P

Operador 2 13.9826 6.9913 11.64 0.000

Catalizador 2 10.1826 5.0913 8.48 0.001

Tiempo 1 1.1852 1.1852 1.97 0.169

Operador*Catalizador 4 4.7741 1.1935 1.99 0.117

Operador*Tiempo 2 2.9137 1.4569 2.43 0.103

Catalizador*Tiempo 2 3.6337 1.8169 3.03 0.061

Operador*Catalizador*Tiempo 4 4.9074 1.2269 2.04 0.109

Error 36 21.6133 0.6004

Total 53 63.1926

S = 0.774836 R-Sq = 65.80% R-Sq(adj) = 49.65%

De estos datos podemos ver que ninguna de las interacciones muestra un efecto significativo para un nivel de significancia de 0.05. Sin embargo, el valor P para BC es 0.0610; por ello, debe de ignorarse (catalizador, tiempo de lavado).

Regresar