Análisis de Cúmulos (cluster).
El
análisis de cúmulos, también llamado segmentación o análisis taxonómico es una
forma de hacer una partición de un conjunto de objetos, en cúmulos, de tal
suerte de que los objetos en el mismo cúmulo comparte un perfil mientras los
objetos en otro cúmulo tiene un perfil totalmente diferente.
El
análisis de cúmulos puede llevarse a cabo en cualquier base de datos. Los
sujetos en la base de datos deben tener propiedades que puedan ser valoradas de
forma numérica.
Procedimiento
para encontrar los cúmulos.
1.-
Encontrar la similitud o disimilitud entre cada par de objetos en la base de
datos. En este paso, usted debe calcular las distancias entre objetos usando una
función de distancia. La métrica más utilizada en la euclidiana la cual mide la
distancia entre dos puntos en el espacio utilizando la siguiente ecuación
d2 = (x1 – x2)2
+ (y1 – y2)2 + … + (z1 – z2)2
2.-
Agrupe los objetos en un árbol binario de jerarquía de cúmulos. En este paso,
usted debe agrupar, los objetos que se encuentran próximos. Una forma de hacer
esto es ordenar las distancias entre pares de objetos de acuerdo a la
proximidad que existe entre.
3.-
Determine donde debe dividir el árbol de jerarquía de cúmulos.
Ejemplo 1.
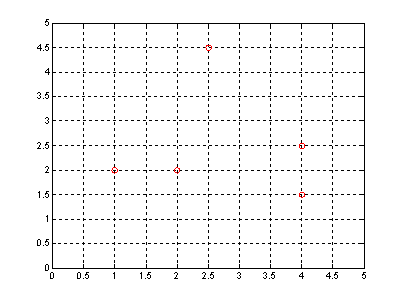
Considere
un conjunto de datos, C, el cual esta constituido por 5 objetos donde cada uno
tiene las siguientes coordenadas.
|
objeto |
x |
y |
|
1 |
1 |
2 |
|
2 |
2.5 |
4.5 |
|
3 |
2 |
2 |
|
4 |
4 |
1.5 |
|
5 |
4 |
2.5 |
los
cuales se muestran en la siguiente figura.
1.-
Calculamos una matriz donde tenemos la información de la distancia entre los
puntos de la siguiente forma
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
0.0000 |
2.9155 |
1.0000 |
3.0414 |
3.0414 |
|
2 |
2.9155 |
0.0000 |
2.5495 |
3.3541 |
2.5000 |
|
3 |
1.0000 |
2.5495 |
0.0000 |
2.0616 |
2.0616 |
|
4 |
3.0414 |
3.3541 |
2.0616 |
0.0000 |
1.0000 |
|
5 |
3.0414 |
2.5000 |
2.0616 |
1.0000 |
0.0000 |
2.-
Ordenamos las distancias entre objetos de menor a mayor
1.0000
3.0000 1.0000
4.0000
5.0000 1.0000
3.0000
4.0000 2.0616
3.0000
5.0000 2.0616
2.0000
5.0000 2.5000
2.0000
3.0000 2.5495
2.0000
4.0000 2.9155
1.0000
4.0000 3.0414
1.0000
5.0000 3.0414
2.0000
4.0000 3.3541
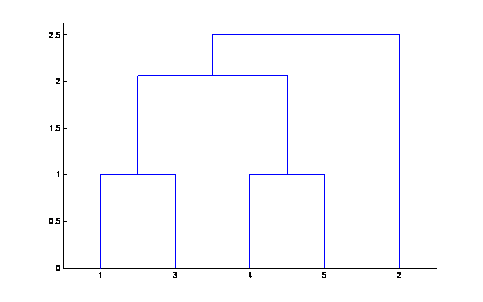
Ligamos los datos que se
encuentran mas cerca, para mostrar este procedimiento hacemos una gráfica
Este
procedimiento puede llevarse a cabo en MATLAB de la siguiente forma.
Dados
los datos.
1.-
Calculamos la distancia entre los objetos utilizando
Y
= pdist([x,
y]); % calcula las distancias entre los objetos.
squareform(Y) % da la informacion en forma de matriz
La
función pdist por default
calcula la distancia euclidiana pero puede calcular otras medidas de distancia.
2.-
Hacemos el ligado de objetos con la función
Z
= linkage(Y); % hace el ligado de los objetos
dendrogram(Z); % hace una
grafica de las objetos ligados
3.-
Para decidir los cúmulos utilizamos la función
T
= CLUSTER(Z, 0.8)
donde Z
son los valores ligados y el 0.8 indica el umbral al cual se quiere hacer la
separación de cúmulos.
Análisis de MINITAB
Para
llevar a cabo el análisis de cúmulos en MINITAB ir al menú
Stat >
Multivariate > Cluster Observations …
Al
seleccionar este menú aparece la caja de diálogo
Al
llenar esta caja de diálogo obtenemos los siguientes resultados
Diferentes distancias
Distancia Euclidiana
La
distancia euclidiana en tres dimensiones con p1 en (x1, y1,
z1) y p2 en (x2, y2
,z2) esta definida por
d2 = (x1 – x2)2 + (y1
– y2)2 + … + (z1
– z2)2
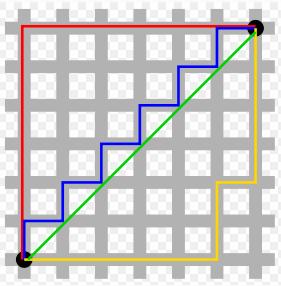
Distancia Manhattan
La
distancia entre dos puntos es media a los largo de los eje ortogonales. En un
plano con p1 en (x1, y1) y p2 en (x2,
y2), La distancia Manhattan es |x1
- x2| + |y1 - y2|. En la siguiente figura se
ve en rojo como es calculada la distancia Manhattan.
Distancia de Pearson
Esta
distancia esta basada en el coefficiente de
correlación de Pearson el cuas
es calculada a partir de valores muestrales y su
desviación estandar. El coeficiente de correlación r
toma valores desde –1 (correlación negativa mas grande) a +1 (correlación
positiva mas grande).
La
distancia de Perrazo dp es calculada como dp = 1 - r y este esta entre 0 y 2.
Ejemplo 2
Genere
una secuencia de datos aleatorios en MATLAB, con medias 1, 2 y 3 y haga el
análisis de cúmulos.
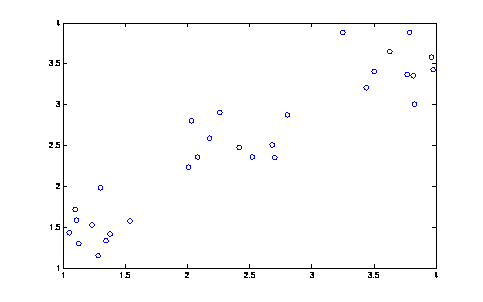
rand('seed', 3);
X = [rand(10,2)+1;
rand(10,2)+2; rand(10,2)+3];
plot(X(:,1), X(:,2), 'o');
Y
= pdist(X);
Z
= linkage(Y);
dendrogram(Z);
En
MINITAB
Para
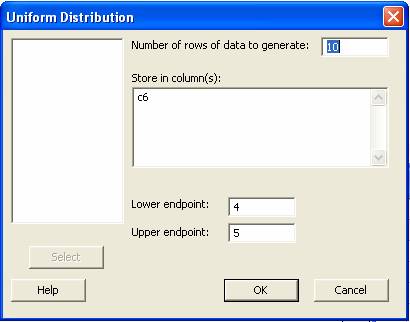
generar datos con una distribución uniforme entre 0 y 1 hacer
Ir
al meú Calc > Random Data > Uniform …
Cuando
aparece la caja de dialogo hacer
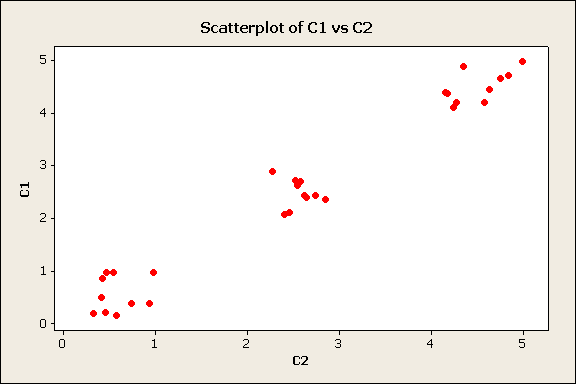
Los
valores graficados con MINITAB lucen como
Graph
> Scatterplot …
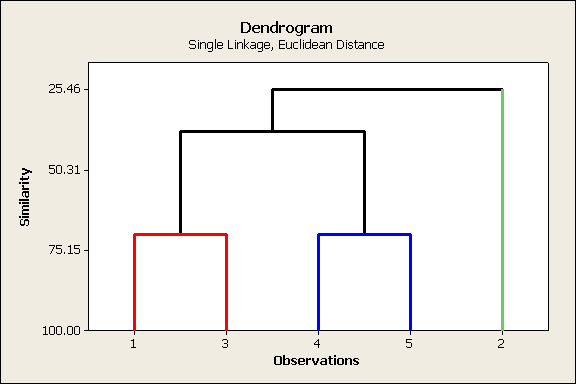
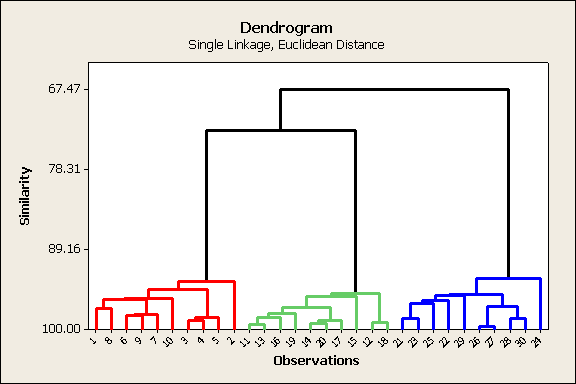
El dendrograma
resultante en MINITAB luce como
Ejemplo 3.
Tenemos
la información nutricional de 12 cereales, tales como, proteínas,
carbohidratos, grasas, calorías y Vitamina A. Deseamos hacer un análisis de
cúmulos para saber que cereales tienen propiedades similares.
|
Cereal |
Proteínas |
Carbohidratos |
Grasas |
Calorías |
vitamina A |
|
Life |
6 |
19 |
1 |
110 |
0 |
|
Grape Nuts |
3 |
23 |
0 |
100 |
25 |
|
Super Sugar Crisp |
2 |
26 |
0 |
110 |
25 |
|
Special K |
6 |
21 |
0 |
110 |
25 |
|
Rice Krispies |
2 |
25 |
0 |
110 |
25 |
|
Raisin Bran |
3 |
28 |
1 |
120 |
25 |
|
Product 19 |
2 |
24 |
0 |
110 |
100 |
|
Wheaties |
3 |
23 |
1 |
110 |
25 |
|
Total |
3 |
23 |
1 |
110 |
100 |
|
Puffed Rice |
1 |
13 |
0 |
50 |
0 |
|
Sugar Corn Pops |
1 |
26 |
0 |
110 |
25 |
|
Sugar Smacks |
2 |
25 |
0 |
110 |
25 |
Utilizando
MATLAB hacemos:
X
= [
6 19 1 110 0
3 23 0 100 25
2 26 0 110 25
6 21 0 110 25
2 25 0 110 25
3 28 1 120 25
2 24 0 110 100
3 23 1 110 25
3 23 1 110 100
1 13 0 50 0
1 26 0 110 25
2 25 0 110 25];
Y
= pdist(X);
Z
= linkage(Y);
dendrogram(Z);
c
= cophenet(Z,
Y)
[[1:12]',
cluster(Z, 6)]
Los
resultados obtenidos son:
La
correlación de los datos utilizando la métrica euclidiana fue 0.9726, lo cual
indica, que hicimos uso de una buena medida de comparación.
El
dendrogram es:
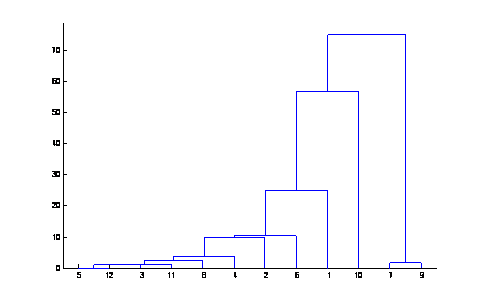
y
considerando 6 cúmulos, tenemos los siguientes grupos.
|
cúmulo |
Cereal |
Proteínas |
Carbohidratos |
Grasas |
Calorías |
vitamina A |
|
4 |
Life |
6 |
19 |
1 |
110 |
0 |
|
1 |
Grape Nuts |
3 |
23 |
0 |
100 |
25 |
|
2 |
Super Sugar Crisp |
2 |
26 |
0 |
110 |
25 |
|
2 |
Special K |
6 |
21 |
0 |
110 |
25 |
|
2 |
Rice Krispies |
2 |
25 |
0 |
110 |
25 |
|
3 |
Raisin Bran |
3 |
28 |
1 |
120 |
25 |
|
6 |
Product 19 |
2 |
24 |
0 |
110 |
100 |
|
2 |
Wheaties |
3 |
23 |
1 |
110 |
25 |
|
6 |
Total |
3 |
23 |
1 |
110 |
100 |
|
5 |
Puffed Rice |
1 |
13 |
0 |
50 |
0 |
|
2 |
Sugar Corn Pops |
1 |
26 |
0 |
110 |
25 |
|
2 |
Sugar Smacks |
2 |
25 |
0 |
110 |
25 |
Results
for: CEREAL.MTW
Cluster
Analysis of Observations: Proteina, Carbo, Grasa, Calorias
Euclidean Distance, Single Linkage
Amalgamation Steps
Number
of obs.
Number of Similarity
Distance Clusters New
in new
Step clusters level
level joined cluster
cluster
1 11
100.000 0.0000 5
12 5 2
2 10
100.000 0.0000 8
9 8 2
3 9
98.604 1.0000 3
11 3 2
4 8
98.604 1.0000 5
7 5 3
5 7
98.604 1.0000 3
5 3 5
6 6
97.582 1.7321 3
8 3 7
7 5
96.878 2.2361 1
4 1
2
8 4
94.776 3.7417 1
3 1 9
9 3
85.969 10.0499 1
2 1 10
10 2
85.625 10.2956 1
6 1 11
11 1
28.754 51.0294 1 10
1 12
Final Partition
Number of clusters: 5
Within Average Maximum
cluster distance distance
Number of sum of
from from
observations squares
centroid centroid
Cluster1 2 2.5
1.11803 1.11803
Cluster2 1 0.0
0.00000 0.00000
Cluster3 7 14.0
1.27053 1.92725
Cluster4 1 0.0
0.00000 0.00000
Cluster5 1 0.0 0.00000
0.00000
Cluster Centroids
Grand
Variable Cluster1 Cluster2
Cluster3 Cluster4 Cluster5
centroid
Proteina 6.0 3
2.143 3 1
2.833
Carbo 20.0 23
24.571 28 13
23.000
Grasa 0.5 0
0.286 1 0
0.333
Calorias 110.0
100 110.000 120 50
105.000
Distances Between
Cluster Centroids
Cluster1 Cluster2
Cluster3 Cluster4 Cluster5
Cluster1 0.0000 10.8743
5.9851 13.1624 60.6156
Cluster2 10.8743
0.0000 10.1630 20.6398
51.0294
Cluster3 5.9851
10.1630 0.0000 10.6301
61.1170
Cluster4 13.1624
20.6398 10.6301 0.0000
71.6240
Cluster5 60.6156
51.0294 61.1170 71.6240
0.0000
Dendrogram
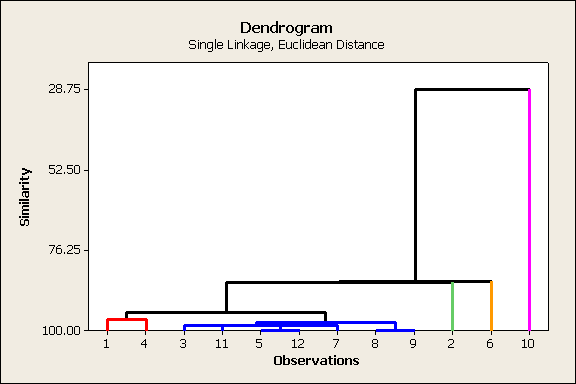
|
N |
Cereal |
Proteínas |
Carbohidratos |
Grasas |
Calorías |
vitamina A |
|
1 |
Life |
6 |
19 |
1 |
110 |
0 |
|
2 |
Grape Nuts |
3 |
23 |
0 |
100 |
25 |
|
3 |
Super Sugar Crisp |
2 |
26 |
0 |
110 |
25 |
|
4 |
Special K |
6 |
21 |
0 |
110 |
25 |
|
5 |
Rice Krispies |
2 |
25 |
0 |
110 |
25 |
|
6 |
Raisin Bran |
3 |
28 |
1 |
120 |
25 |
|
7 |
Product 19 |
2 |
24 |
0 |
110 |
100 |
|
8 |
Wheaties |
3 |
23 |
1 |
110 |
25 |
|
9 |
Total |
3 |
23 |
1 |
110 |
100 |
|
10 |
Puffed Rice |
1 |
13 |
0 |
50 |
0 |
|
11 |
Sugar Corn Pops |
1 |
26 |
0 |
110 |
25 |
|
12 |
Sugar Smacks |
2 |
25 |
0 |
110 |
25 |
Ejemplo
4.
Una
de las aplicaciones del análisis de cúmulos es el filtrado y segmentación de
imágenes. Las imágenes son representadas por arreglos bidimensionales, cada
punto (píxel) almacena la información del tono de gris tal como se muestra en
la siguiente imagen.
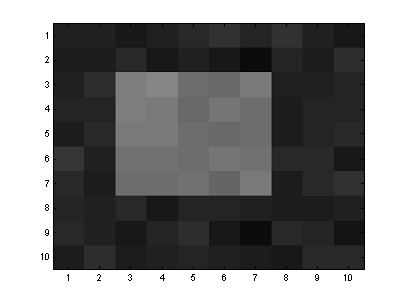
Note
que la imagen esta corrompida por ruido y deseamos encontrar las dos regiones
principales. El código en MATLAB es:
Img = zeros(10, 10) + 10;
for n=3:7
for m=3:7
Img(n,m) = 30;
end;
end;
for n=1:10
for m=1:10
Img(n,m) = Img(n,m) + normrnd(0,2);
end;
end;
figure(1)
colormap(gray)
image(Img)
X = [];
for m=1:10
X = [X; Img(m, :)'];
end;
X
= [X, zeros(100, 1)];
Y
= pdist(X);
Z = linkage(Y);
T = cluster(Z, 2);
Img2 = [];
n = 1;
for m=1:10
Img2 = [Img2; T(n: m*10)'];
n = n + 10;
end;
figure(2)
colormap(gray)
image(Img2*10)
Los
resultados al aplicar el análisis de cúmulos, considerando a priori que existen
solo dos clases o cúmulos es:
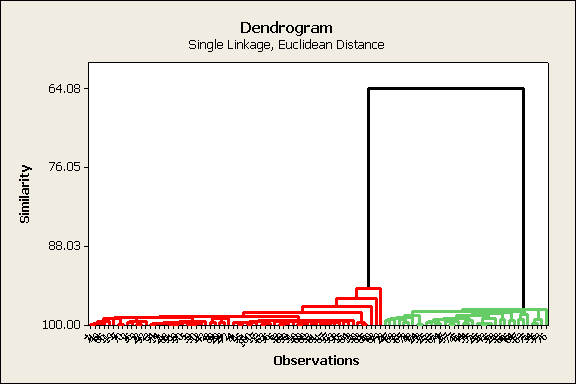
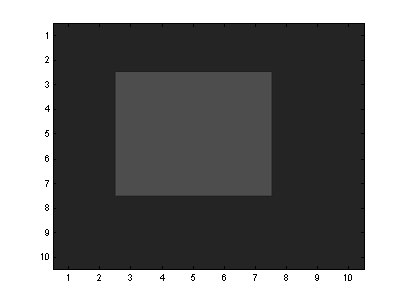
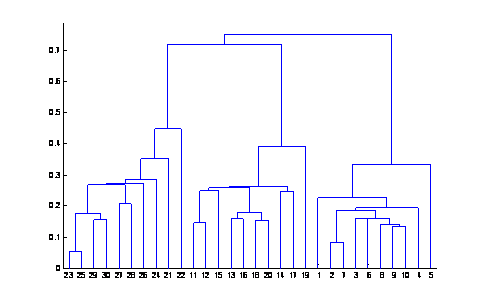
Ejemplo 5.
Con
el objetivo de ver como se comporta la separabilidad
entre dos clases, a medida que aumenta el ruido, tomar los datos del ejemplo
anterior (archivo imagen.mtw) y hacer el dendrograma
para diferentes niveles de ruido. El ruido que agregaremos es generado por una
distribución normal con media cero y varianza variable. Comenzaremos con una
valor de sigma = 0.0 y aumentaremos el valor de sigma con incrementos unitarios
(sigma = {0, 1, 2, 3, 4, …}).