Solución de
algunos ejemplos Utilizando MINITAB
Regresión
múltiple.
MINITAB es un
programa de propósito general para realizar estudio de datos. A continuación se
presenta un conjunto de ejemplos y la solución calculada con MINITAB.
Ejemplo 01.
Se midió el
porcentaje de sobre vivencia de cierto tipo de semen animal, después del
almacenamiento, en varias combinaciones de concentraciones de tres materiales
que se utilizan para aumentar su oportunidad de sobre vivencia. Los datos son:
|
x1 (peso %) |
x2 (peso %) |
x3 (peso %) |
y (% sobre vivencia) |
|
1.74 |
5.3 |
10.8 |
25.5 |
|
6.32 |
5.42 |
9.4 |
31.2 |
|
6.22 |
8.41 |
7.2 |
25.9 |
|
10.52 |
4.63 |
8.5 |
38.4 |
|
1.19 |
11.6 |
9.4 |
18.4 |
|
1.22 |
5.85 |
9.9 |
26.7 |
|
4.1 |
6.62 |
8 |
26.4 |
|
6.32 |
8.72 |
9.1 |
25.9 |
|
4.08 |
4.42 |
8.7 |
32 |
|
4.15 |
7.6 |
9.2 |
25.2 |
|
10.15 |
4.83 |
9.4 |
39.7 |
|
1.72 |
3.12 |
7.6 |
35.7 |
|
1.7 |
5.3 |
8.2 |
26.5 |
Determinar el modelo lineal y verifique, utilizando análisis de varianza que efectivamente el modelo depende linealmente de la variables propuestas.
Results
for: semen_animal.MTW
Regression
Analysis: y versus x1, x2, x3
The
regression equation is
y = 39.2 + 1.02 x1 - 1.86 x2 - 0.343 x3
Predictor
Coef SE Coef T P
Constant
39.157 5.887 6.65
0.000
x1
1.0161 0.1909 5.32
0.000
x2
-1.8616 0.2673 -6.96
0.000
x3 -0.3433 0.6171 -0.56 0.592
S = 2.073
R-Sq = 91.2% R-Sq(adj) =
88.2%
Analysis of Variance
Source
DF SS MS F P
Regression
3 399.45 133.15 30.98 0.000
Residual Error
9 38.68 4.30
Total
12 438.13
Source
DF Seq SS
x1
1 187.31
x2
1 210.81
x3
1 1.33
Unusual Observations
Obs
x1 y Fit SE Fit Residual St Resid
5 1.2 18.400 15.545 1.579 2.855 2.13R
12 1.7 35.700 32.488 1.465 3.212 2.19R
R denotes an observation with a large standardized
residual
Stepwise Regression: y versus x1, x2, x3
Forward selection.
Alpha-to-Enter: 0.01
Response
is y on 3 predictors, with
N = 13
Step 1 2
Constant
42.21 36.09
x2
-2.09 -1.87
T-Value
-4.21 -7.26
P-Value
0.001 0.000
x1 1.03
T-Value 5.65
P-Value
0.000
S
3.90 2.00
R-Sq
61.75 90.87
R-Sq(adj)
58.27 89.04
C-p
30.0 2.3
Regression Analysis: y versus x1, x2
The regression equation is
y = 36.1 + 1.03 x1 - 1.87 x2
Predictor Coef SE Coef T P
Constant
36.095 2.012 17.94
0.000
x1
1.0305 0.1825 5.65
0.000
x2 -1.8696
0.2576 -7.26 0.000
S = 2.000
R-Sq = 90.9% R-Sq(adj) =
89.0%
Analysis of Variance
Source
DF SS MS F P
Regression
2 398.12 199.06 49.76 0.000
Residual Error
10 40.01 4.00
Total
12 438.13
Source
DF Seq SS
x1
1 187.31
x2
1 210.81
Unusual Observations
Obs
x1 y Fit SE Fit Residual St Resid
5 1.2 18.400 15.633 1.516 2.767 2.12R
12 1.7 35.700 32.034 1.174 3.666 2.26R
R denotes an observation with a large standardized
residual
Ejemplo 02.
Considere los datos de la siguiente tabla,
donde se tomaron mediciones de nueve niños. El propósito del experimento fue
llegar a una ecuación de estimación adecuada que relacionara la estatura de un
niño con todas o un subconjunto de variables independientes. Encuentre el modelo lineal utilizando
regresión por selección hacia adelante.
|
Edad |
Estaura al nacer |
Peso al nacer |
Talla del torax al
nacer |
Estatura del niño |
|
x1 (días) |
x2 (cm) |
x3 (kg) |
x4 (cm) |
y (cm) |
|
78.00 |
48.20 |
2.75 |
29.50 |
57.50 |
|
69.00 |
45.50 |
2.15 |
26.30 |
52.80 |
|
77.00 |
46.30 |
4.41 |
32.20 |
61.30 |
|
88.00 |
49.00 |
5.52 |
36.50 |
67.00 |
|
67.00 |
43.00 |
3.21 |
27.20 |
53.50 |
|
80.00 |
48.00 |
4.32 |
27.70 |
62.70 |
|
74.00 |
48.00 |
2.31 |
28.30 |
56.20 |
|
94.00 |
53.00 |
4.30 |
30.30 |
68.50 |
|
102.00 |
58.00 |
3.71 |
28.70 |
69.20 |
Regression Analysis:
Estatura versus Edad, Est al nacer, ...
The regression equation is
Estatura = 7.1 + 0.100 Edad + 0.726 Est al nacer + 3.08
Peso al nacer
- 0.030
Talla torax
Predictor
Coef SE Coef T P
Constant 7.15 16.46 0.43 0.687
Edad
0.1001 0.3397 0.29
0.783
Est al n
0.7264 0.7859 0.92
0.408
Peso al
3.076 1.059 2.90
0.044
Talla to
-0.0300 0.1665 -0.18
0.866
S = 0.8610
R-Sq = 99.1% R-Sq(adj) =
98.2%
Analysis of Variance
Source
DF SS MS F P
Regression
4 318.274 79.569 107.32 0.000
Residual Error
4 2.966 0.741
Total
8 321.240
Source
DF Seq SS
Edad
1 288.147
Est al n 1
23.870
Peso al
1 6.233
Talla to
1 0.024
Stepwise Regression: Estatura versus Edad, Est al
nacer, ...
Forward selection.
Alpha-to-Enter: 0.01
Response is
Estatura on 4 predictors, with N = 9
Step 1 2
Constant
19.01 20.11
Edad
0.518 0.414
T-Value
7.81 14.43
P-Value
0.000 0.000
Peso al
2.03
T-Value
6.82
P-Value
0.000
S
2.17 0.794
R-Sq
89.70 98.82
R-Sq(adj)
88.23 98.43
C-p
39.6 2.1
Regression Analysis: Estatura versus Edad, Peso al nacer
The regression equation is
Estatura = 20.1 + 0.414 Edad + 2.03 Peso al nacer
Predictor
Coef SE Coef T P
Constant
20.108 1.987 10.12
0.000
Edad 0.41363 0.02866 14.43 0.000
Peso al
2.0253 0.2971 6.82
0.000
S = 0.7942
R-Sq = 98.8% R-Sq(adj) =
98.4%
Analysis of Variance
Source
DF SS MS F P
Regression
2 317.46 158.73 251.65 0.000
Residual Error
6 3.78 0.63
Total
8 321.24
Source
DF Seq SS
Edad
1 288.15
Peso al
1 29.31
Ejemplo 03.
La tensión de la pierna es un ingrediente necesario para un pateador exitoso en el futbol americano. Una medida de la calidad de una buena patada es el “tiempo de suspensión”. Este es el tiempo que el balón permanece en el aire antes de que el sea atrapado por el regresador de la patada. Para determinar cuales factores de tensión de la pierna influyen en el tiempo de suspensión y desarrollar un modelo empírico para predecir esta respuesta, el Departamento de Salud, Educación Física y Recreación del Instituto Politécnico y la Universidad de Virginia, llevó a cabo el estudio “La relación entre el desempeño físico y la habilidad de patear”. Se eligieron 13 pateadores para el experimento y cada uno pateó 10 veces el balón. El tiempo promedio de suspensión, junto con las medidas de tensión se usaron en el análisis, se registraron como sigue.
RLS
|
LLS |
RHF |
LHF |
POTENCIA |
TIEMPO |
|
170 |
170 |
106 |
106 |
240.57 |
4.75 |
|
140 |
130 |
92 |
93 |
195.49 |
4.07 |
|
180 |
170 |
93 |
78 |
152.99 |
4.04 |
|
160 |
160 |
103 |
93 |
197.09 |
4.18 |
|
170 |
150 |
104 |
93 |
266.56 |
4.35 |
|
150 |
150 |
101 |
87 |
260.56 |
4.16 |
|
170 |
180 |
108 |
106 |
219.25 |
4.43 |
|
110 |
110 |
86 |
92 |
132.68 |
3.2 |
|
120 |
110 |
90 |
86 |
130.24 |
3.02 |
|
130 |
120 |
85 |
80 |
205.88 |
3.64 |
|
120 |
140 |
89 |
83 |
153.92 |
3.68 |
|
140 |
130 |
92 |
94 |
154.64 |
3.6 |
|
160 |
150 |
95 |
95 |
240.57 |
3.85 |
Cada variable de regresión se define como
- RLS, tensión de la pierna derecha (libras)
- LLS, tensión de la pierna izquierda (libras)
- RHF, flexibilidad del músculo del tendón de la corva derecha (grados)
- LHF, flexibilidad del músculo del tendón de la corva izquierda (grados)
- Potencia, tensión total de la pierna (libras pie)
Determinar los mejores conjuntos de variables que describen el modelo de regresión lineal.
Best
Subsets Regression: TIEMPO versus RLS, LLS, RHF, LHF, POTENCIA
Response is TIEMPO
P
O
T
E
N
R L R L C
L L H H I
Vars
R-Sq R-Sq(adj) C-p S S S F F A
1 74.3 72.0
6.2 0.25864 X
1 71.4 68.8
8.0 0.27298 X
2 87.1 84.6
0.6 0.19211 X
X
2 80.4 76.5
4.6 0.23697 X X
3 88.2 84.2
2.0 0.19418 X
X X
3 87.6 83.4
2.4 0.19909 X X
X
4 88.2 82.3
4.0 0.20558 X X
X X
4 88.2 82.2
4.0 0.20596 X X X X
5
88.2 79.8 6.0
0.21978 X X X X X
Ejemplo 04.
En el departamento de pesca y fauna del Instituto Politécnico y la Universidad de Virginia se llevo a cabo un experimento para estudiar el efecto de las características de la corriente sobre la biomasa de peses. Las variables de regresión son:
x1 : Profundidad promedio
x2 : áreas de refugio de la corriente
x3 : porcentaje de cubierta de boveda
x4 : área >=25 centímetros de profundidad.
y : biomasa.
|
x1 |
x2 |
x3 |
x4 |
y |
|
14.3 |
15 |
12.2 |
48 |
100 |
|
19.1 |
29.4 |
26 |
152.2 |
388 |
|
54.6 |
58 |
24.2 |
469.7 |
755 |
|
28.8 |
42.6 |
26.1 |
485.9 |
1288 |
|
16.1 |
15.9 |
31.6 |
87.6 |
230 |
|
10 |
56.4 |
23.3 |
6.9 |
0 |
|
28.5 |
95.1 |
13 |
192.9 |
551 |
|
13.8 |
60.6 |
7.5 |
105.8 |
345 |
|
10.7 |
35.2 |
40.3 |
0 |
0 |
|
25.9 |
52 |
40.3 |
116.6 |
348 |
a) ajuste una regresión lineal múltiple que incluya las cuatro variables
b) Determine el conjunto de variables que mejor determinan a la biomasa, utilizando el método por pasos hacia delante.
c) Utilice Cp, R2 y s2 para determinar el mejor subconjunto de variables.
Regression Analysis: y versus x1, x2, x3, x4
The regression equation is
y = 86 - 15.9 x1 + 2.42 x2 + 1.83 x3 + 3.07 x4
Predictor
Coef SE Coef T P
Constant
85.8 125.2 0.68
0.524
x1
-15.933 5.143 -3.10
0.027
x2
2.423 1.648 1.47
0.202
x3
1.828 3.292 0.56
0.603
x4
3.0738 0.3739 8.22
0.000
S = 101.7
R-Sq = 96.3% R-Sq(adj) =
93.3%
Analysis of Variance
Source
DF SS MS F P
Regression
4 1330434 332609 32.16 0.001
Residual Error
5 51706 10341
Total
9 1382141
Source
DF Seq SS
x1
1 617547
x2
1 633
x3
1 13201
x4
1 699054
Unusual Observations
Obs
x1 y Fit SE Fit Residual St Resid
3 54.6 755.0 844.3 92.8 -89.3 -2.14R
R denotes an observation with a large standardized residual
Stepwise Regression: y versus x1, x2, x3, x4
Forward selection.
Alpha-to-Enter: 0.01
Response
is y on 4 predictors, with
N = 10
Step 1
Constant
48.09
x4
2.12
T-Value
8.01
P-Value
0.000
S
138
R-Sq
88.90
R-Sq(adj)
87.52
C-p
8.8
Stepwise Regression: y versus x1, x2, x3, x4
Forward selection.
Alpha-to-Enter: 0.01
Response
is y on 4 predictors, with
N = 10
Step 1
Constant 48.09
x4
2.12
T-Value
8.01
P-Value
0.000
S
138
R-Sq
88.90
R-Sq(adj)
87.52
C-p
8.8
Best Subsets Regression: y versus x1, x2, x3, x4
Response is y
x x x x
Vars
R-Sq R-Sq(adj) C-p S 1 2 3 4
1 88.9 87.5
8.8 138.46 X
1 44.7 37.8
67.9 309.15 X
2 94.6 93.1
3.2 102.85 X
X
2 89.0 85.9
10.6 147.07 X
X
3 96.0 94.0
3.3 95.649 X X
X
3 94.6 92.0
5.2 111.09 X
X X
4 96.3 93.3
5.0 101.69 X X X X
Análisis
de Varianza
Ejemplo 11.
Suponga que un
experimento industrial un ingeniero está interesado en cómo la absorción media
de humedad en concreto varía entre cinco mezclas diferentes de concreto. Las
muestras se exponen a la humedad por 48 horas y se decide que se prueben seis
muestras para cada mezcla, por lo que se requiere probar un total de 30
muestras. Los datos de este experimento se muestran en la siguiente tabla.
|
Mezcla |
1 |
2 |
3 |
4 |
5 |
|
|
551.00 |
595.00 |
639.00 |
417.00 |
563.00 |
|
|
457.00 |
580.00 |
615.00 |
449.00 |
631.00 |
|
|
450.00 |
508.00 |
511.00 |
517.00 |
522.00 |
|
|
731.00 |
583.00 |
573.00 |
438.00 |
613.00 |
|
|
499.00 |
633.00 |
648.00 |
415.00 |
656.00 |
|
|
632.00 |
517.00 |
677.00 |
555.00 |
679.00 |
Determine :
a) Si las medias de cada mezcla son iguales
b) y que grupos de medias son iguales.
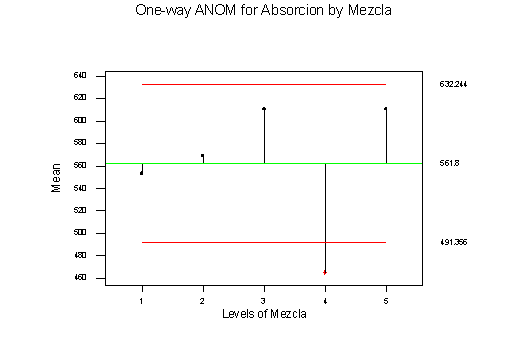
One-way ANOVA: Absorcion versus Mezcla
Analysis of Variance for Absorcio
Source
DF SS MS F P
Mezcla 4 85356
21339 4.30 0.009
Error 25 124020 4961
Total 29 209377
Individual 95% CIs For Mean
Based on Pooled StDev
Level
N Mean StDev
----------+---------+---------+------
1 6
553.33 110.15 (------*-------)
2 6 569.33
47.99
(------*-------)
3 6 610.50
59.95
(------*-------)
4 6 465.17
57.61 (------*-------)
5 6
610.67 58.78 (------*-------)
----------+---------+---------+------
Pooled StDev =
70.43 480 560 640
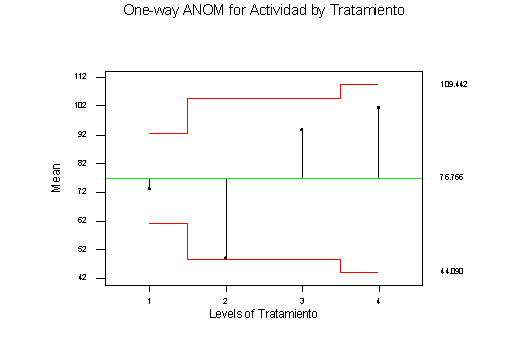
Ejemplo
12
Parte de un estudio que se llevo a cabo en el Instituto Politécnico y Universidad Estatal de Virginia, se diseño para medir los niveles de actividad de fosfatasa alcalina en suero de niños con crisis convulsivas que reciben terapia contra convulsiones bajo el cuidado de un médico particular. Se encontraron 45 sujetos para estudio y se clasificaron en cuatro grupos según el medicamento administrado :
G-1 : Control (No reciben anticonvulsivos y no tienen historial de crisis convulsivas)
G-2 : Fenobartibal.
G-3 : Carbanacepina.
G-4 : Otros anticonvulsivos.
Se determinó el nivel de actividad de la fosfatasa alcalina en suero a partir de muestras sanguíneas obtenidas de cada sujeto y se registraron en la siguiente tabla. Pruebe la hipótesis al nivel de significancia de 0.05 de que el nivel promedio de actividad de fosfatasa alcalina en suero es el mismo para los cuatro grupos.
|
Nivel de Actividad de fosfatasa alcalina en suero |
||||
|
G-1 |
G-2 |
G-3 |
G-4 |
|
|
49.20 |
97.50 |
97.07 |
62.10 |
110.60 |
|
44.54 |
105.00 |
73.40 |
94.95 |
57.10 |
|
45.80 |
58.05 |
68.50 |
142.50 |
117.60 |
|
95.84 |
86.60 |
91.85 |
53.00 |
77.71 |
|
30.10 |
58.35 |
106.60 |
175.00 |
150.00 |
|
36.50 |
72.80 |
0.57 |
79.50 |
82.90 |
|
82.30 |
116.70 |
0.79 |
29.50 |
115.50 |
|
87.85 |
45.15 |
0.77 |
78.40 |
|
|
105.00 |
70.35 |
0.81 |
127.50 |
|
|
95.22 |
77.40 |
|
|
|
Determine :
a) Si las medias de cada mezcla son iguales
b) y que grupos de medias son iguales.
Results
for: fosfatasa_suero.MTW
One-way ANOVA:
Actividad versus Tratamiento
Analysis of Variance for Activida
Source
DF SS MS F P
Tratamie 3 14136 4712 3.61 0.021
Error 41 53474 1304
Total 44 67609
Individual 95% CIs For Mean
Based on Pooled StDev
Level
N Mean StDev
--+---------+---------+---------+----
1 20 73.01
25.75 (----*-----)
2 9 48.93
47.11 (-------*-------)
3 9 93.61
46.57
(-------*-------)
4 7 101.63
31.02
(--------*--------)
--+---------+---------+---------+----
Pooled StDev =
36.11 30 60 90 120