1.- El archivo potencia_diaria.mtw, contiene información de la potencia promedio diaria consumida por un sistema de distribución. El archivo contiene un consecutivo correspondiente al día, la fecha con la hora en que se realizo la medición y la potencia consumida en Watts.

a) Se desea hacer el análisis de regresión y ver si en posible ajustar un modelo lineal que permita predecir la potencia en función del día.

Solución

La ecuación de regresión utilizando MINITAB es

Potencia = 312 - 0.074 Dia

b) Hacer el análisis de varianza con un nivel de significancia de 0.05 para ver si el modelo es adecuado.

Hipótesis

H0 : b es igual a cero

H1 : b es diferente de cero

Análisis de varianza

Fuente GL SC MC F P

Regresión 1 1312 1312 0.18 0.671

Error residual 2974 21657026 7282

Total 2975 21658338

Análisis de variancia para probar b =0
Fuente de variación	Suma de cuadrados	Grados de libertad	Cuadrado medio	f calculada
Regresión	1312	1	1312	0.18
Error	21657026	2974	7282
Total	21658338	2975
rechazamos b=0, al nivel de significancia a cuando f > 3.84

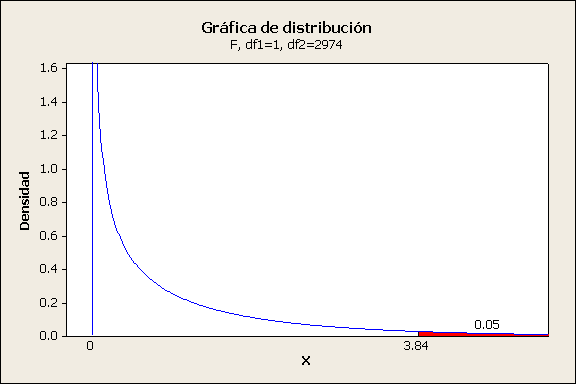
Podemos ver que el resultado de la f calculada es de 0.18 y la desigualdad 0.18>3.84 no se cumple, nos encontramos en la región de aceptar la Ho, por lo tanto no existe evidencia suficiente para rechazar Ho, y se acepta. Tenemos un dato adicional el valor P, Este valor indica que la hipótesis Ho (b=0) es valida con nivel de significancía de 67.1 % muy superior al valor que deseamos del 5%. Por lo tanto la hipótesis nula se acepta y no existe evidencia de dependencia lineal en el nivel de significancia de 5%.

c) Si el modelo es valido hacer la predicción para el día 32.

El modelo no es valido.

2.- La resistencia a la tracción de una unión de alambre es una característica importante. El archivo resistencia.mtw, brinda información sobre la resistencia a la tracción y, la altura del molde x₁, la altura del perno x₂, la altura del lazo x₃, longitud del alambre x₄, ancho de la unión sobre el molde x₅ y ancho del molde sobre el perno x₆.

a) Ajuste un modelo de regresión usando todas las variables independientes y concluya acerca del modelo utilizando análisis de varianza con un nivel de significancia de 0.05.

La ecuación de regresión es

y = 3.14 + 0.644 x1 - 0.010 x2 + 0.505 x3 - 0.120 x4 - 2.46 x5 + 1.50 x6

Predictor Coef Coef. de EE T P

Constante 3.137 8.110 0.39 0.706

x1 0.6444 0.5889 1.09 0.295

x2 -0.0104 0.2677 -0.04 0.970

x3 0.5046 0.1423 3.55 0.004

x4 -0.11967 0.05623 -2.13 0.055

x5 -2.462 2.598 -0.95 0.362

x6 1.504 1.519 0.99 0.342

S = 0.894074 R-cuad. = 71.1% R-cuad.(ajustado) = 56.7%

Análisis de varianza

Fuente GL SC MC F P

Regresión 6 23.6286 3.9381 4.93 0.009

Error residual 12 9.5924 0.7994

Total 18 33.2211

nos interesa probar la hipótesis

H0 : b1=b2=b3=b4=b5=b6 es igual a cero

Análisis de variancia para probar b =0
Fuente de Variación	Suma de cuadrados	Grados de libertad	Cuadrado medio	f calculada
Regresión	23.6286	6	3.9381	4.93
Error	9.5924	12	0.7994
Total	33.2211	18
rechazamos b=0, al nivel de significancia a cuando f > 3

Rechazamos Ho porque se cumple la desigualdad 4.93>3, de la prueba de hipótesis utilizando MINITAB podemos ver que el valor de P es 0.009 se encuentra debajo de nuestro nivel de significancia de 0.05 por lo tanto la hipótesis Ho se rechaza. Esto significa que hay suficiente evidencia de dependencia lineal.

b) Use regresión por pasos con un nivel de significancia de 0.05 y calcule el mejor subconjunto.

Regresión paso a paso: y vs. x1, x2, x3, x4, x5, x6

Alfa a entrar: 0.15 Alfa a retirar: 0.15

La respuesta es y en 6 predictores, con N = 19

Paso 1 2

Constante -8.971 4.656

x3 0.59 0.51

Valor T 3.94 3.91

Valor P 0.001 0.001

x4 -0.124

Valor T -2.78

Valor P 0.013

S 1.01 0.855

R-cuad. 47.72 64.76

R-cuad.(ajustado) 44.65 60.35

Cp de Mallows 6.7 1.6

El mejor subconjunto es x3 y x4

c) Calcule el subconjunto de variables que mejor modelan utilizando el criterio Cp.

Regresión de los mejores subconjuntos: y vs. x1, x2, x3, x4, x5, x6

la respuesta es y

R-cuad. Cp de x x x x x x

Vars R-cuad. (ajustado) Mallows S 1 2 3 4 5 6

1 47.7 44.6 6.7 1.0107 X

1 31.1 27.0 13.6 1.1606 X

2 64.8 60.4 1.6 0.85541 X X

2 57.2 51.8 4.8 0.94318 X X

3 67.3 60.7 2.6 0.85151 X X X

3 67.1 60.6 2.7 0.85319 X X X

4 68.7 59.8 4.0 0.86141 X X X X

4 68.6 59.6 4.1 0.86350 X X X X

5 71.1 60.0 5.0 0.85905 X X X X X

5 69.0 57.0 5.9 0.89056 X X X X X

6 71.1 56.7 7.0 0.89407 X X X X X X

Utilizando el criterio Cp los mejores subconjuntos son X3 y X4

d) Con el nuevo modelo subconjunto de variables calcule el modelo de regresión y realice el análisis de varianza con un nivel de significancia de 0.05

Análisis de regresión: y vs. x3, x4

La ecuación de regresión es

y = 4.66 + 0.511 x3 - 0.124 x4

Predictor Coef Coef. de EE T P

Constante 4.656 6.395 0.73 0.477

x3 0.5113 0.1308 3.91 0.001

x4 -0.12418 0.04466 -2.78 0.013

S = 0.855415 R-cuad. = 64.8% R-cuad.(ajustado) = 60.4%

Análisis de varianza

Fuente GL SC MC F P

Regresión 2 21.513 10.757 14.70 0.000

Error residual 16 11.708 0.732

Total 18 33.221

nos interesa probar la hipótesis

H₀: b₃ = b₄ = 0

Análisis de variancia para probar B3 = B4 = 0
Fuente de Variación	Suma de Cuadrados	Grados de libertad	Cuadrado medio	f calculada
Regresión	21.513	2	10.757	14.70
Error	11.708	16	0.732
Total	33.2211	18
rechazamos H0, al nivel de significancia a cuando f > 3.63

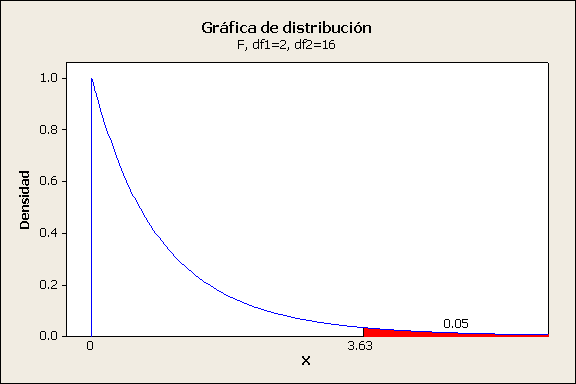
Rechazamos Ho porque se cumple la desigualdad 14.70>3.63, de la prueba de hipótesis. Utilizando MINITAB podemos ver que el valor de P es 0.000 se encuentra debajo de nuestro nivel de significancia de 0.05 por lo tanto la hipótesis Ho se rechaza. Esto significa que hay suficiente evidencia de dependencia lineal.

e) Calcule el intervalo de confianza utilizando el modelo calculado en el inciso (d) y los valores x1=5.5 x2 = 20, x3 =32.1, x4 = 94, x5 = 2.2 y x5 =2.1.

Solución:

Sustituyendo los valores en la ecuación

y = 4.66 + 0.511 (32.1) - 0.124 (94)

y = 9.4071

Un intervalo de confianza de 95% para la respuesta media m_y|x3,x4 es

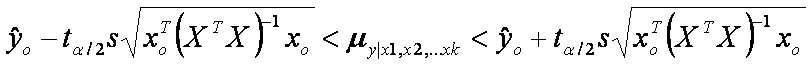
donde t_a/2 es un valor de la distribución t con 16 grados de libertad.

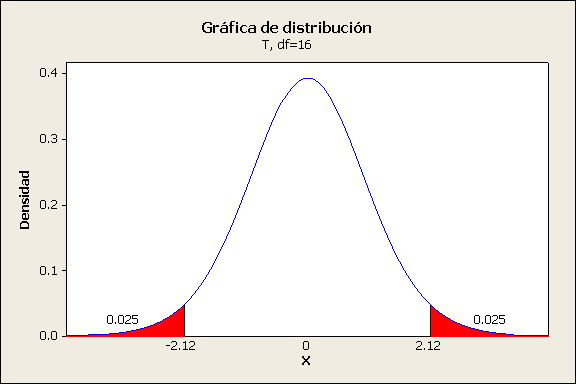
t_a/2 = 2.12

X = [ 29.6 94.9

32.4 89.7

31.0 96.2

32.4 95.6

28.6 86.5

30.6 84.5

32.4 88.8

32.6 85.7

32.2 93.6

31.8 86.0

32.6 87.1

33.4 93.1

31.8 83.4

32.4 94.5

31.4 83.4

33.2 85.2

35.4 84.1

34.0 86.9

34.2 83.0 ]

x_o = [32.1, 94]^T

x_o'(X’X)^-1x_o = 0.0929

s =0.8554

9.4071 – (2.12)(0.8554)sqrt(0.0929) < m < 9.4071 +(2.12)(0.8554) sqrt(0.0929)

8.8545 < m < 9.9597

3.- En un sistema trifásico de potencia es deseable que los voltajes en cada una de las fases sea igual para garantizar el balance del sistema. Para probar esto se hicieron mediciones de los voltajes y se almacenaron en el archivo voltaje.mtw. Este archivo contiene dos columnas una correspondiente a la fase (1, 2, 3) y la otra a los valores de voltaje en volts. Para estas mediciones y con el objeto de verificar el equilibro:

a) Calcular la media y varianza de cada fase,

Estadísticas descriptivas: voltaje

Variable fase Media Varianza

voltaje 1 13538 7823

2 13577 8717

3 13638 10948

b) probar si las medias de los voltajes son iguales con un nivel de significancia de 0.05,

H₀ : m₁ = m₂ = m₃

H₁ : al menos dos de las medias no son iguales.

ANOVA unidireccional: voltaje vs. fase

Fuente GL SC MC F P

fase 2 150672 75336 8.22 0.001

Error 87 797134 9162

Total 89 947806

S = 95.72 R-cuad. = 15.90% R-cuad.(ajustado) = 13.96%

ICs de 95% individuales para la media

basados en Desv.Est. agrupada

Nivel N Media Desv.Est. ---------+---------+---------+---------+

1 30 13538.3 88.4 (------*------)

2 30 13577.5 93.4 (-----*------)

3 30 13637.8 104.6 (------*-----)

---------+---------+---------+---------+

13550 13600 13650 13700

Desv.Est. agrupada = 95.7

Análisis de variancia para probar m1 = m2 = m3
Fuente de variación	Suma de cuadrados	Grados de Libertad	Cuadrado medio	f calculada
Regresión	150672	2	75336	8.22
Error	797134	87	9162
Total	947806	89
rechazamos H0, al nivel de significancia 0.05 cuando f >fa[k-1, k(n-1)]

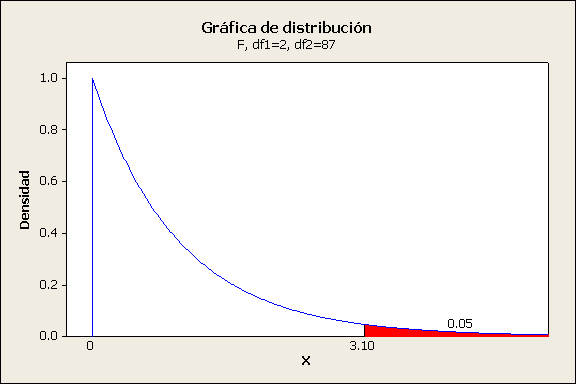
Rechazamos Ho porque se cumple la desigualdad 8.22>3.10, de la prueba de hipótesis, utilizando MINITAB podemos ver que el valor de P es 0.001 se encuentra debajo de nuestro nivel de significancia de 0.05 por lo tanto la hipótesis Ho se rechaza. Esto significa que hay suficiente evidencia de que las medias son diferentes.

c) hacer un análisis de medias y decir que conjunto de medias son similares

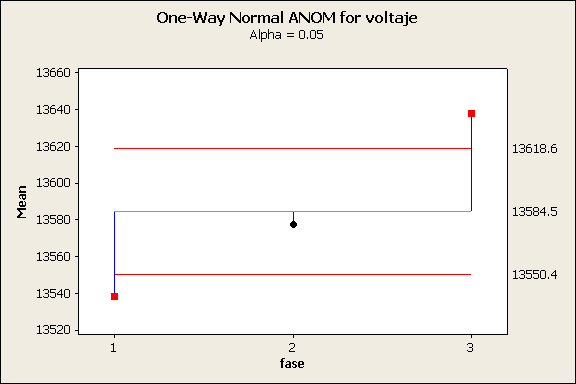13550 13600 13650 13700

Ninguna media es igual para el nivel de significancia.

d) hacer la prueba de Barlett para probar que los voltajes tienen la misma varianza

Deseamos probar la hipótesis nula

H₀ :

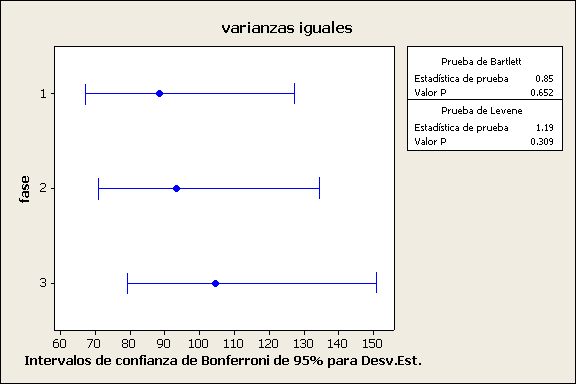
Prueba de varianzas iguales: voltaje vs. fase

Intervalos de confianza de Bonferroni de 95% para desviaciones estándares

fase N Inferior Desv.Est. Superior

1 30 67.1417 88.446 127.560

2 30 70.8756 93.365 134.654

3 30 79.4283 104.631 150.903

Prueba de Bartlett (distribución normal)

Estadística de prueba = 0.85, valor p = 0.652

Del valor P=0.652 mayor que nuestro nivel de significancia de 0.05 podemos concluir que se rechaza la hipotesis nula Ho, por lo tanto las varianzas son iguales.

4.- El archivo potencia_diaria.mtw contiene la información correspondiente a las potencias diaria de un sistema de potencia tomadas durante un mes a intervalos de 15 minutos. Con esta información y en un nivel de significancia de 0.05 :

a) Calcular la media y varianza de potencia por dia,

Resultados para: POTENCIA_DIARIA.MTW

Estadísticas descriptivas: Potencia

Variable Dia N Media Varianza

Potencia 1 96 351.8 9983.4

2 96 294.52 2723.77

3 96 232.04 829.53

4 96 366.0 11447.2

5 96 339.09 6979.35

6 96 344.56 8547.99

7 96 328.36 7415.02

8 96 349.29 8341.34

9 96 277.80 2168.37

10 96 228.24 666.04

11 96 287.07 2260.94

12 96 303.18 2061.55

13 96 306.59 1918.58

14 96 306.14 2105.02

15 96 303.00 2226.23

16 96 266.43 561.34

17 96 240.29 514.78

18 96 358.2 10098.4

19 96 355.26 8697.61

20 96 359.96 8892.37

21 96 350.39 6898.26

22 96 342.59 6466.07

23 96 278.47 1619.05

24 96 218.92 588.26

25 96 343.34 8499.29

26 96 352.59 8574.74

27 96 342.76 9507.40

28 96 342.64 9388.48

29 96 353.48 8976.44

30 96 283.59 2612.92

31 96 220.91 1046.44

b) probar si las medias de las potencias son iguales,

La hipótesis a probar es H₀ : m₁ = m₂ = m₃

ANOVA unidireccional: Potencia vs. Dia

Fuente GL SC MC F P

Dia 30 6209796 206993 39.46 0.000

Error 2945 15448543 5246

Total 2975 21658338

S = 72.43 R-cuad. = 28.67% R-cuad.(ajustado) = 27.95%

Análisis de variancia para probar m1 = m2 = m3
Fuente de variación	Suma de cuadrados	Grados de Libertad	Cuadrado medio	f calculada
Regresión	6209796	30	206993	39.46
Error	15448543	2945	5246
Total	21658338	2975
rechazamos H0, al nivel de significancia 0.05 cuando f >fa[k-1, k(n-1)]

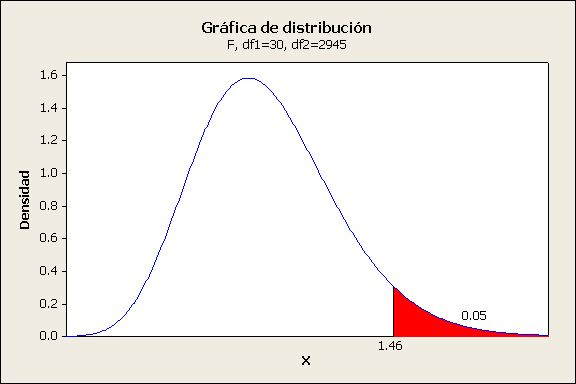
Rechazamos Ho porque se cumple la desigualdad 39.46>1.46, de la prueba de hipótesis, utilizando MINITAB podemos ver que el valor de P es 0.000 se encuentra debajo de nuestro nivel de significancia de 0.05 por lo tanto la hipótesis Ho se rechaza. Esto significa que hay suficiente evidencia de que las medias son diferentes.

c) hacer un análisis de medias y decir que conjunto de medias son similares

d) hacer la prueba de Barlett para probar que las potencias tienen la misma varianza

Deseamos probar la hipótesis nula

H₀ :

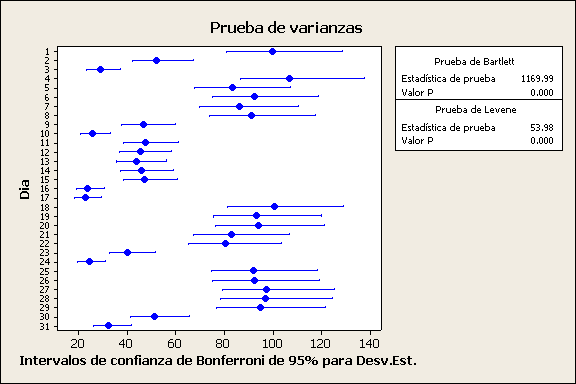
Prueba de varianzas iguales: Potencia vs. Dia

Intervalos de confianza de Bonferroni de 95% para desviaciones estándares

Dia N Inferior Desv.Est. Superior

1 96 81.0182 99.917 128.543

2 96 42.3183 52.190 67.142

3 96 23.3538 28.802 37.053

4 96 86.7547 106.992 137.644

5 96 67.7408 83.542 107.477

6 96 74.9677 92.455 118.943

7 96 69.8230 86.111 110.780

8 96 74.0560 91.331 117.496

9 96 37.7580 46.566 59.906

10 96 20.9263 25.808 33.201

11 96 38.5555 47.549 61.172

12 96 36.8162 45.404 58.412

13 96 35.5167 43.802 56.350

14 96 37.2024 45.880 59.025

15 96 38.2585 47.183 60.700

16 96 19.2113 23.693 30.480

17 96 18.3974 22.689 29.189

18 96 81.4833 100.491 129.280

19 96 75.6210 93.261 119.979

20 96 76.4630 94.299 121.315

21 96 67.3461 83.056 106.850

22 96 65.2023 80.412 103.449

23 96 32.6267 40.237 51.765

24 96 19.6665 24.254 31.203

25 96 74.7539 92.192 118.604

26 96 75.0850 92.600 119.129

27 96 79.0630 97.506 125.440

28 96 78.5670 96.894 124.653

29 96 76.8236 94.744 121.887

30 96 41.4482 51.117 65.761

31 96 26.2300 32.349 41.616

Prueba de Bartlett (distribución normal)

Estadística de prueba = 1169.99, valor p = 0.000

Del valor P=0.000 se encuentra debajo de nuestro nivel de significancia de 0.05 por lo tanto la hipótesis Ho se rechaza. Esto significa que hay suficiente evidencia de que las varianzas son diferentes.

Regresar