1.- Los científicos del Departamento de Patología Vegetal en el Tecnológico de Virginia Tech, realizaron un experimento en el que se aplicaron 5 tratamientos diferentes a 6 localidades distintas de un huerto de manzanas, para determinar si había diferencias significativas en el crecimiento según el tratamiento. Los tratamientos 1 a 4 presentan distintos herbicida y el 5 es un control. El periodo de crecimiento fue mayo a noviembre de 1982, y el crecimiento nuevo, medido en centímetros, para muestras seleccionadas de 6 ubicaciones en el huerto, se registra como sigue.

	Ubicaciones
Tratamiento	1	2	3	4	5	6
1	455	72	61	215	695	501
2	622	82	444	170	437	134
3	695	56	50	443	701	373
4	607	650	493	257	490	262
5	388	263	185	103	518	622

Determine con un nivel de significancia de 0.05 y para un modelo y_ij = m + a_i + b_j

Results for: huerto.MTW

Two-way ANOVA: crecimiento versus Ubicaciones, Tratamiento

Source DF SS MS F P

Ubicaciones 5 634335 126867 3.68 0.016

Tratamiento 4 79630 19908 0.58 0.682

Error 20 689107 34455

Total 29 1403071

S = 185.6 R-Sq = 50.89% R-Sq(adj) = 28.78%

Two-way ANOVA: crecimiento versus Ubicaciones, Tratamiento

Source DF SS MS F P

Ubicaciones 5 634335 126867 3.68 0.016

Tratamiento 4 79630 19908 0.58 0.682

Error 20 689107 34455

Total 29 1403071

S = 185.6 R-Sq = 50.89% R-Sq(adj) = 28.78%

Individual 95% CIs For Mean Based on

Pooled StDev

Ubicaciones Mean -------+---------+---------+---------+--

1 553.4 (--------*-------)

2 224.6 (-------*--------)

3 246.6 (-------*--------)

4 237.6 (--------*--------)

5 568.2 (-------*--------)

6 378.4 (--------*--------)

-------+---------+---------+---------+--

200 400 600 800

Individual 95% CIs For Mean Based on

Pooled StDev

Tratamiento Mean -------+---------+---------+---------+--

1 333.167 (------------*------------)

2 314.833 (------------*------------)

3 386.333 (------------*------------)

4 459.833 (------------*------------)

5 346.500 (------------*------------)

-------+---------+---------+---------+--

240 360 480 600

a) si existen diferencias significativas entre las medias de los tratamientos

Ho: Los valores de alfa son iguales a cero o no existen diferencias significativas entre las medias de los tratamientos

De acuerdo con el valor P = 0.682 y dado nuestro valor de significancia de 0.05 tenemos que la hipótesis se acepta y por lo tanto no existen diferencias significativas entre las medias de los tratamientos.

b) si existen diferencias significativas entre las medias de Ubicación.

Ho: Los valores de beta son iguales a cero o no existen diferencias significativas entre las medias de Ubicación

De acuerdo con el valor P = 0.016 y dado nuestro valor de significancia de 0.05 tenemos que la hipótesis se rechaza y por lo tanto existen diferencias significativas entre las medias de Ubicación.

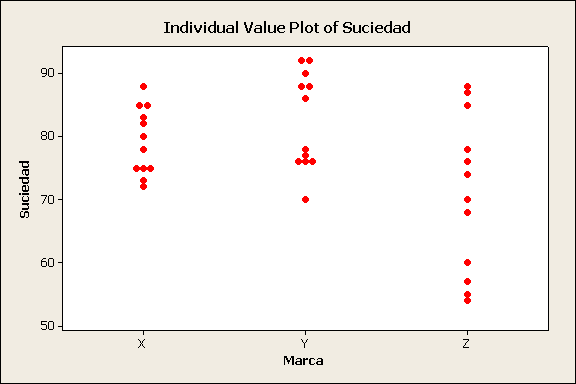
2.- Considere combinaciones de tres factores en el retiro de suciedad de cargas estándar de lavandería. El primer factor es la marca de detergente: X, Y, o Z. El segundo factor es el tipo de detergente: líquido o en polvo. El Tercer factor es la temperatura del agua, caliente o tibia. El experimento se repitió tres veces. La respuesta esta expresada en la remoción porcentual de la suciedad. Los datos son los siguientes.

Marca	Tipo	Temperatura
X	En polvo	Caliente	85	88	80
		Tibia	82	83	85
	Líquido	Caliente	78	75	72
		Tibia	75	75	73
Y	En polvo	Caliente	90	92	92
		Tibia	88	86	88
	Líquido	Caliente	78	76	70
		Tibia	76	77	76
Z	En polvo	Caliente	85	87	88
		Tibia	76	74	78
	Líquido	Caliente	60	70	68
		Tibia	55	57	54

Los resultados aplicando anova son

Results for: suciedad.MTW

ANOVA: Suciedad versus Temperatura, Tipo, Marca

Factor Type Levels Values

Temperatura fixed 2 Caliente, tibia

Tipo fixed 2 En polvo, Liquido

Marca fixed 3 X, Y, Z

Analysis of Variance for Suciedad

Source DF SS MS F P

Temperatura 1 160.44 160.44 22.39 0.000

Tipo 1 1906.78 1906.78 266.06 0.000

Marca 2 833.72 416.86 58.17 0.000

Temperatura*Tipo 1 9.00 9.00 1.26 0.274

Temperatura*Marca 2 187.06 93.53 13.05 0.000

Tipo*Marca 2 200.72 100.36 14.00 0.000

Temperatura*Tipo*Marca 2 15.17 7.58 1.06 0.363

Error 24 172.00 7.17

Total 35 3484.89

S = 2.67706 R-Sq = 95.06% R-Sq(adj) = 92.80%

a) ¿Existe efectos significativos de la interacción, con el nivel a = 0.05?

De acuerdo con el resultado tenemos que

Temperatura*Marca 2 187.06 93.53 13.05 0.000

Tipo*Marca 2 200.72 100.36 14.00 0.000

Existe interacción entre Temperatura*Marca y Tipo*Marca dado que ambos tienen un valor P = 0.000 y la hipótesis debe ser rechazada.

b) ¿Hay diferencias significativas entre las tres marcas de detergente?

Si hay diferencias significativa dado que el valor P = 0 y por lo tanto las medias son diferentes para diferentes marcas de detergente.

Marca 2 833.72 416.86 58.17 0.000

c) ¿Cuál combinación de factores preferiría utilizar?

De acuerdo con el análisis individual de las medias por marca podemos ver que en promedio la que tiene mejor remoción es la Marca de detergente Y y todas sus combinaciones. En particular en polvo con temperatura caliente.

Regresar