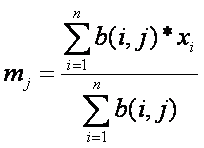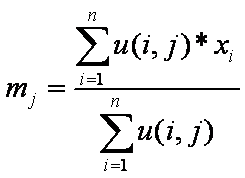El algoritmo de k-medias.

Suponga que tenemos n características en vectores x₁, x₂, ..., x_n, donde cada x, está representado en un espacio m dimensional y sabemos que están agrupados en k cúmulos (k<n). Definimos m_j como la media del j-ésimo cúmulo. Si los cúmulos están bien separados, podemos usar una mínima distancia de clasificación para separarlos. Esto es, podemos decir que x_i esta en el j-ésimo cúmulo si || x_i – m_j || es el mínimo con respecto a los k cúmulos. Esto sugiere el siguiente algoritmo para encontrar la k medias:

· Haga una estimación inicial para la k medias m₁, m₂, ..., m_k.

· Mientras no cambie alguna media:

o Use la media estimada para clasificar los datos en cúmulos. b(i,j) = 1 si el i-ésimo dato, es el más cercano a la j-ésima media.

o Para cada uno de los cúmulos

§ Calcule la nueva media m_i, utilizando la nueva clasificación

o fin.

· fin.

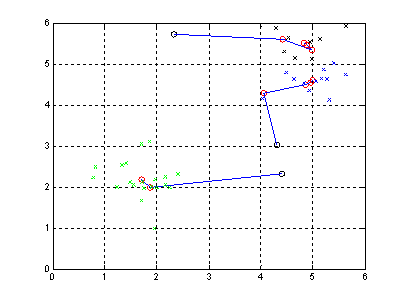
Aquí tenemos un ejemplo que muestra las dos medias como se mueven en el procedimiento para calcular las medias.

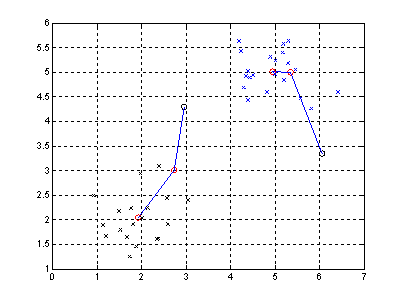
Este es un ejemplo simple del algoritmo de k-medias. Este puede ser visto como un algoritmo voraz para particionar en k cúmulos, el cual la suma de las distancias al cuadrado, al centro de caca cúmulo. Pero este algoritmo tiene algunas debilidades.

· La manera de inicializar no se especifica. Una forma común es comenzar seleccionado aletoriamento k medias de los ejemplos.

· Los resultados dependerán del valor inicial de las medias y frecuentemente pasa que particiones subóptimas son encontradas. La solución estándar es calculada atizando diferentes puntos de arranque.

· Puede pasar que un conjunto de ejemplos cercano a una media este vacío, por lo que no puede ser modificada. Esto es un inconveniente del método y debe ser manejado en la implementación, pero puede ser ignorado.

· Los resultados depende de la métrica utilizada para medir || x - m_i ||. Una solución popular es normalizar cada variable por la desviación estándar, aunque no siempre es deseable.

· La solución de pende del número de cúmulos seleccionado.

El ultimo problema es particularmente pesado, normalmente no tenemos manera de saber cuantos cúmulos existen.

En el ejemplo mostrado enseguida, el conjunto de datos es inicializado utilizando 3 medias. ¿Esto es mejor o peor que cuando se utilizando únicamente 2 medias? La respuesta puede solo encontrarse utilizando diferentes clasificadores o uniendo algunas subclases en un procedimiento posterior.

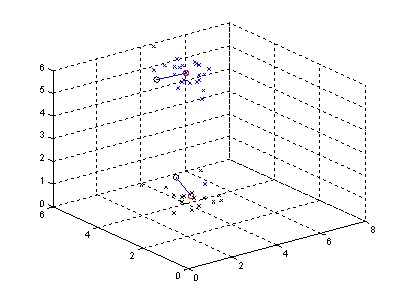
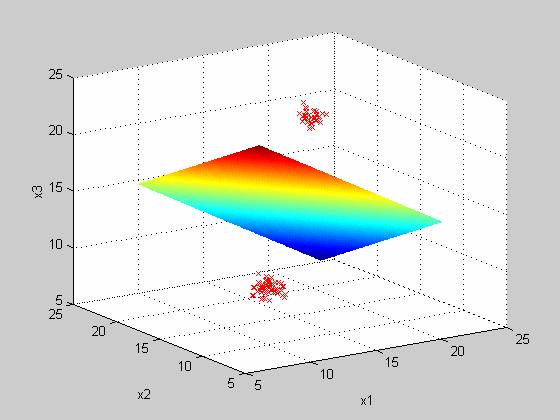
El algoritmo puede calcular medias en cualquier dimensión, a continuación se presenta un ejemplo del algoritmo de k medias aplicado en tres dimensiones.

A continuación se da el código para hacer el llamado a una función implementada en MATLAB, para llamar a la función de kmedias.

clear;

for n = 1 :40

if(unifrnd(0,1) > 0.5)

x(n) = normrnd(2, 0.5);

y(n) = normrnd(2, 0.5);

z(n) = normrnd(2, 0.5);

else

x(n) = normrnd(5, 0.5);

y(n) = normrnd(5, 0.5);

z(n) = normrnd(5, 0.5);

end;

end

datos = [x', y', z'];

%datos = [x', y'];

[medias, b ] = kmeans(datos, 2)

dim = length(datos(1, :));

for k=1:length(x)

switch(b(k))

case 1

if (dim == 2) plot(datos(k,1), datos(k,2), 'kx'), end;

if (dim == 3) plot3(datos(k,1), datos(k,2), datos(k,3), 'kx'), end;

case 2

if (dim == 2) plot(datos(k,1), datos(k,2), 'bx'), end;

if (dim == 3) plot3(datos(k,1), datos(k,2), datos(k,3), 'bx'), end;

case 3

if (dim == 2) plot(datos(k,1), datos(k,2), 'gx'), end;

if (dim == 3) plot3(datos(k,1), datos(k,2), datos(k,3), 'gx'), end;

end;

end;

hold off;

La función para calcular la k-medias es:

function [medias, b] = kmeans(datos, num_medias)

ndatos = length(datos(:,1));

dim = length(datos(1,:));

if (dim == 2) plot(datos(:,1), datos(:,2), 'x'), end;

if (dim == 3) plot3(datos(:,1), datos(:,2), datos(:,3), 'x'), end;

hold on;

grid on;

medias = zeros(num_medias, dim);

np = zeros(num_medias, dim);

for n = 1: num_medias

for m = 1:dim

medias(n,m) = unifrnd( min(datos(:, m)), max(datos(:, m)) );

end;

end;

medias_old = medias;

if (dim == 2) plot(medias(:,1), medias(:,2), 'ko'); end;

if (dim == 3) plot3(medias(:,1), medias(:,2), medias(:,3), 'ko'), end;

for iter = 1 :100

for k = 1: ndatos

dist = distancia(datos(k,:), medias(1, :));

b(k) = 1;

for ii = 2 :num_medias

aux = distancia(datos(k,:), medias(ii, :));

if( dist > aux)

b(k) = ii;

dist = aux;

end;

end;

end;

medias = zeros(num_medias, dim);

np = zeros(num_medias, dim);

for k = 1 : ndatos

n = b(k);

for m = 1: dim

medias(n, m ) = medias(n,m) + datos(k, m);

np(n,m) = np(n,m) +1;

end;

end;

for n=1: num_medias

for m = 1 :dim

if( np(n,m) ~= 0)

medias(n, m) = medias(n,m) /np(n,m);

else

medias(n,m) = 0;

end;

end;

end;

if (dim == 2) plot(medias(:,1), medias(:,2), 'ro'), end;

if (dim == 3) plot3(medias(:,1), medias(:,2), medias(:,3),'ro'), end;

if (max(max(abs(medias_old - medias)))<0.01)

break;

end;

for n = 1: num_medias

if (dim == 2) plot([medias(n,1), medias_old(n,1)],[medias(n,2), medias_old(n, 2)]), end;

if (dim == 3) plot3([medias(n,1), medias_old(n,1)],[medias(n,2), medias_old(n, 2)],[medias(n,3), medias_old(n, 3)] ), end;

end;

medias_old = medias;

end;

function d = distancia(dx, media)

d = 0;

n = length(dx);

for k = 1: n

d = d + (dx(k) - media(k))^2;

end;

d = d^0.5;

Algoritmo de K-medias en MINITAB

Entrar al menú

Stat > Multivariate > Cluster K-Means

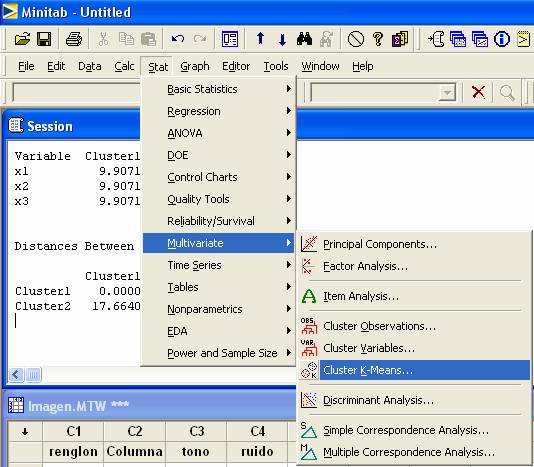
Después aparecerá la caja de dialogó

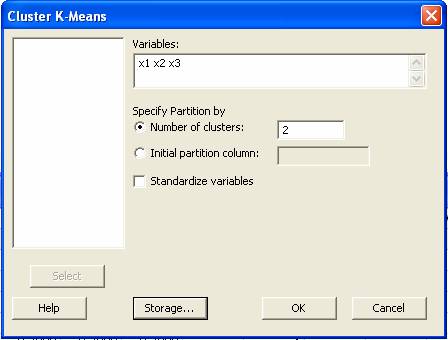
En la opción Storage, espeficar la columna donde quedará la etiqueta de pertenencia, en una caja de dialogo como la siguiente.

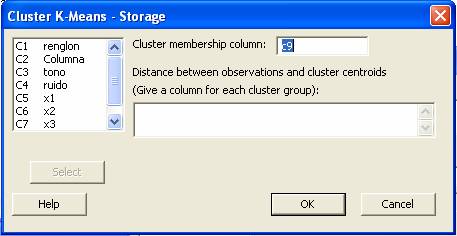
Ejemplo 1.

Tenemos la información nutricional de 12 cereales, tales como, proteínas, carbohidratos, grasas, calorías y Vitamina A. Deseamos hacer un análisis de cúmulos para saber que cereales tienen propiedades similares.

Cereal	Proteínas	Carbohidratos	Grasas	Calorías	vitamina A
Life	6	19	1	110	0
Grape Nuts	3	23	0	100	25
Super Sugar Crisp	2	26	0	110	25
Special K	6	21	0	110	25
Rice Krispies	2	25	0	110	25
Raisin Bran	3	28	1	120	25
Product 19	2	24	0	110	100
Wheaties	3	23	1	110	25
Total	3	23	1	110	100
Puffed Rice	1	13	0	50	0
Sugar Corn Pops	1	26	0	110	25
Sugar Smacks	2	25	0	110	25

La solución en MINITAB es

Cereal	Proteina	Carbo	Grasa	Calorias	VitaminA	clase
Life	6	19	1	110	0	1
Grape Nuts	3	23	0	100	25	3
Super Sugar Crisp	2	26	0	110	25	3
Special K	6	21	0	110	25	4
Rice Krispies	2	25	0	110	25	3
Raisin Bran	3	28	1	120	25	6
Product 19	2	24	0	110	100	5
Wheaties	3	23	1	110	25	3
Total	3	23	1	110	100	5
Puffed Rice	1	13	0	50	0	2
Sugar Corn Pops	1	26	0	110	25	3
Sugar Smacks	2	25	0	110	25	3

El algoritmo de k medias difusas.

Este algoritmo para cálculo de medias es algunas veces llamado duro o crespo, porque cada característica del vector x es al mismo tiempo miembro y no miembro de un cúmulo en particular. Esto es un cúmulo difuso o suave, en el cual cada característica del vector x puede tener un grado de membresía en cada cúmulo. El algoritmo de k medias difusas de Dunn y Bezdek es :

· Haga una estimación inicial para la k medias m₁, m₂, ..., m_k.

· Mientras no cambie alguna media:

o Use la media estimada para encontrar el grado de membresía u(i,j) de el i-ésimo dato x_i, en el j-ésimo cúmulo; por ejemplo, si a(i,j) = exp(- || x_i – m_j ||² ), uno puede usar u(i,j) = a(i,j) / sum_i a(i,j)

o Para cada uno de los cúmulos

§ Calcule la nueva media m_j, utilizando el grado de membresía;

o fin.

· fin.

Ejemplo 2

Repetir el ejemplo de la imagen y calcular el cúmulo al que pertenece cada píxel para diferentes niveles de ruido.

Función Discriminante.

Asumiendo que nuestros datos x, en un espacio de dimensión D, siguen una distribución normal multidimencional dada por

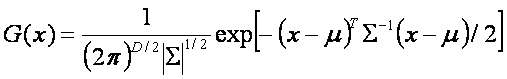
donde m es la media y S la matriz de covarianza.

Definimos

La verosimilitud de un dato dado una distribución

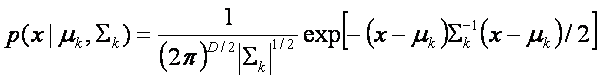
La probabilidad a posteriori utilizando la regla de Bayes, la cual nos da la probabilidad de que la k-ésima distribución genero el dato x, como

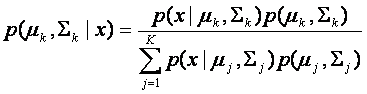
y la probabilidad a priori p(m_k,S_k)

Si asumimos que la probabilidad a priori esta dada por una constante (es la misma para todos los valores) entonces podemos reescribir la probabilidad a posteriori como

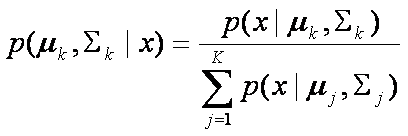
que resulta ser la verosimilitud normalizada.

Un criterio de clasificación estipula que la observación x pertenece a la k-ésima clase si y solo si

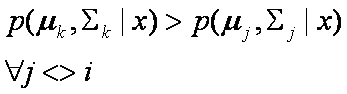
Si consideramos el caso en el cual tenemos la misma varianza y sacando logaritmo natural a ambos lados de la ecuación tenemos

(x-m_k)^TS_k^-1(x-m_k)+ ln(cte) > (x-m_j)^TS_j^-1(x-m_j) ln(cte)

(x-m_k)^T (x-m_k) > (x-m_j)^T (x-m_j)

x^Tx-2m_k^Tx+m_k^T m_k > x^Tx-2m_j^Tx+m_j^T m_j

-2m_k^Tx-m_k^T m_k > -2m_j^Tx+m_j^T m_j

m_kx+b_k> m_jx+b_j

Lo cual nos lleva a una función discriminante lineal dada por m_kx+b_k=y. Si evaluamos esta función podemos decir para un nuevo valor x cual es la clase a la que pertenece.

Para llevar a cabo esta opción en MINITAB hacemos:

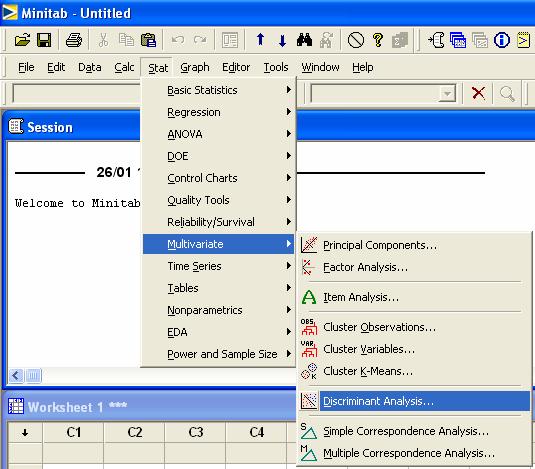
Después aparecerá la caja de diálogo

En la caja de grupos se coloca la columna en donde se encuentra la clasificación dada. En la caja de Predoctores se dan las columnas correspondientes a los valores que caracterizan cada objeto clasificado.

Ejemplo 3

Considere el caso donde existen dos clases. La clase w1 = {2, 2.01, 1.99} y la clase w2 = {3.0, 2.99, 3.01}. Determinar la función discriminante para cada una de las clases

Discriminant Analysis: clase versus valor

Linear Method for Response: clase

Predictors: valor

Group 1 2

Count 3 3

Summary of classification

True Group

Put into Group 1 2

1 3 0

2 0 3

Total N 3 3

N correct 3 3

Proportion 1.000 1.000

N = 6 N Correct = 6 Proportion Correct = 1.000

Squared Distance Between Groups

1 2

1 0.0 10000.0

2 10000.0 0.0

Linear Discriminant Function for Groups

1 2

Constant -20000 -45000

valor 20000 30000

La desigualdad de funciones discriminante resultante es

-2000 + 2000 valor > -4500 + 3000 valor

valor	F1	f2	f1>f2
…	…	…	…
2	2000	1500	1
2.1	2200	1800	1
2.2	2400	2100	1
2.3	2600	2400	1
2.4	2800	2700	1
2.5	3000	3000	*
2.6	3200	3300	0
2.7	3400	3600	0
2.8	3600	3900	0
2.9	3800	4200	0
3	4000	4500	0
…	…	…	…

Si rescribimos la función tenemos

4500-2000 + (2000-3000) valor > 0

2500 – 1000 valor > 0

valor	f1-f2
…	…
2	500
2.1	400
2.2	300
2.3	200
2.4	100
2.5	0
2.6	-100
2.7	-200
2.8	-300
2.9	-400
3	-500
…	…

Si igualamos a cero la función, podemos encontrar de manera analítica la frontera entre clases así

2500 – 1000 valor = 0

valor = 2500/1000

valor = 2.5

En el caso de una sola dimensión tenemos que la frontera resulta ser una constante, en dos dimensiones es una línea recta, en tres dimensiones un plano y en general para más de tres dimensiones es un hiperplano.

Ejemplo 4

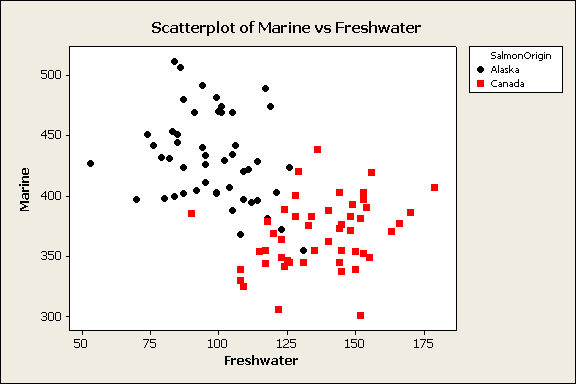
Con el propósito de regular la pesca de salmón es deseable identificar cuando su origen en Alaska o Canada. Cincuenta peses de origen fueron pescados y los anillos de crecimiento fueron medidos cuando ellos vivían en agua fresca y cuando vivían en agua salada. La meta es estar en posibilidades de identificar si nuevos individuos pescados provienen de Alaska o Canada. Los datos para procesar se encuentran en el archivo salmon.mtw y la siguiente figura muestra una grafica de cómo se distribuyen.

a) Calcular las funciones discriminantes lineales de cada clase

b) La función lineal que marca la frontera entre clases

Solución

Discriminant Analysis: SalmonOrigin versus Freshwater, Marine

Linear Method for Response: SalmonOrigin

Predictors: Freshwater, Marine

Group Alaska Canada

Count 50 50

Summary of classification

True Group

Put into Group Alaska Canada

Alaska 44 1

Canada 6 49

Total N 50 50

N correct 44 49

Proportion 0.880 0.980

N = 100 N Correct = 93 Proportion Correct = 0.930

Squared Distance Between Groups

Alaska Canada

Alaska 0.00000 8.29187

Canada 8.29187 0.00000

Linear Discriminant Function for Groups

Alaska Canada

Constant -100.68 -95.14

Freshwater 0.37 0.50

Marine 0.38 0.33

Summary of Misclassified Observations

Squared

Observation True Group Pred Group Group Distance Probability

1** Alaska Canada Alaska 3.544 0.428

Canada 2.960 0.572

2** Alaska Canada Alaska 8.1131 0.019

Canada 0.2729 0.981

12** Alaska Canada Alaska 4.7470 0.118

Canada 0.7270 0.882

13** Alaska Canada Alaska 4.7470 0.118

Canada 0.7270 0.882

30** Alaska Canada Alaska 3.230 0.289

Canada 1.429 0.711

32** Alaska Canada Alaska 2.271 0.464

Canada 1.985 0.536

71** Canada Alaska Alaska 2.045 0.948

Canada 7.849 0.052

a) La función lineal discriminante es

-100.68 + 0.37 Freshwater + 0.38 Marine > -95.14 + 0.5 Freshwater + 0.33 Marine

-5.54 -0.13 Freshwater + 0.05 Marine > 0

b) Si igualamos a cero y despejamos el valor de Marine de la ecuación anterior tenemos

-5.54 -0.13 Freshwater + 0.05 Marine = 0

Marine = (5.54 + 0.13 Freshwater)/ 0.05

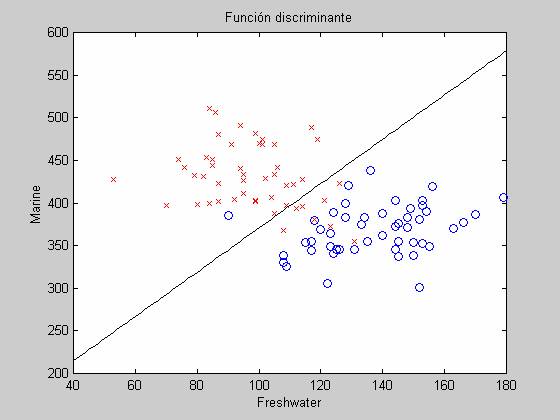
En la siguiente figura en rosa, aparece los puntos de la línea correspondiente a la ecuación Marine = (5.54 + 0.13 Freshwater)/ 0.05, que es donde la función discriminante es igual a cero. Los puntos en azul corresponden a los datos dados.

Ejemplo 5

Una de las aplicaciones del análisis de cúmulos es el filtrado y segmentación de imágenes. Las imágenes son representadas por arreglos bidimensionales, cada punto (píxel) almacena la información del tono de gris tal como se muestra en la siguiente imagen.

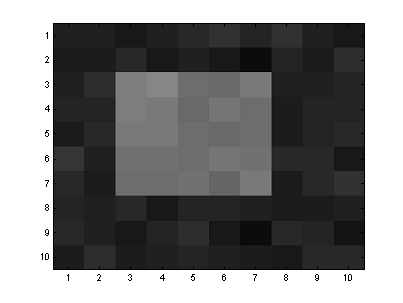
a) Graficar los datos correspondientes a la figura con un nivel de ruido sigma = 0.5

b) Para la información contenida en el archivo imagen.mtw, calcular la función discriminante

Discriminant Analysis: tono versus x1, x2, x3

Linear Method for Response: tono

Predictors: x1, x2, x3

Group 10 20

Count 64 36

Summary of classification

True Group

Put into Group 10 20

10 64 0

20 0 36

Total N 64 36

N correct 64 36

Proportion 1.000 1.000

N = 100 N Correct = 100 Proportion Correct = 1.000

Squared Distance Between Groups

10 20

10 0.00 1142.29

20 1142.29 0.00

Linear Discriminant Function for Groups

10 20

Constant -570.9 -2284.1

x1 35.1 70.0

x2 27.7 55.7

x3 51.3 102.6

c) Graficar la frontera entre las clases dadas

-570.9 + 35.1 x1 + 27.7 x2 + 51.3 x3 > -2284.1 + 70 x1 + 55.7 x2 + 102.6 x3

La función discriminante en la frontera es

1713.2 – 34.9 x1 - 28 x2 - 51.3 x3 = 0

Ejemplo 6

Se tiene información correspondiente a tres clases en un espacio tridimensional, dada en la siguiente tabla. Determinar para dicha información

	w1		w2		w3
n	x1	x2	x1	x2	x1	x2
1	10.49	10.67	10.00	18.96	14.76	21.16
2	10.89	10.38	8.71	19.41	14.38	18.22
3	9.95	11.30	10.23	20.88	15.32	19.51
4	9.60	12.56	11.46	20.13	14.57	17.77
5	10.99	9.62	9.29	19.98	13.83	19.61

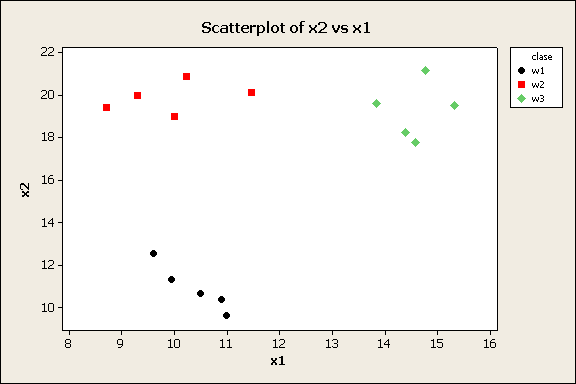
a) Graficar los datos correspondientes a las tres clases

b) Calcular las funciones discriminantes para las tres clases

Results for: segmenta.MTW

Discriminant Analysis: clase versus x1, x2

Linear Method for Response: clase

Predictors: x1, x2

Group w1 w2 w3

Count 5 5 5

Summary of classification

True Group

Put into Group w1 w2 w3

w1 5 0 0

w2 0 5 0

w3 0 0 5

Total N 5 5 5

N correct 5 5 5

Proportion 1.000 1.000 1.000

N = 15 N Correct = 15 Proportion Correct = 1.000

Squared Distance Between Groups

w1 w2 w3

w1 0.0000 68.4786 98.5209

w2 68.4786 0.0000 37.1494

w3 98.5209 37.1494 0.0000

Linear Discriminant Function for Groups

w1 w2 w3

Constant -158.22 -278.50 -376.82

x1 19.38 19.63 27.65

x2 10.56 18.21 18.21

c) a que clase pertenece una observación dada por x =[16.1, 17,4]^T

f1 = -158.22 + 19.38 (16.1) + 10.56 (17.4) = 337.542

f2 = -278.50 + 19.63 (16.1) + 18.21 (17.4) = 354.397

f3 = -376.82 + 27.65 (16.1) + 18.21 (17.4) = 385.199

De acuerdo con los valores calculados el máximo es la función en f3, por lo tanto la clase resultante es w3.

Regresar.