Transformaciones Geométricas
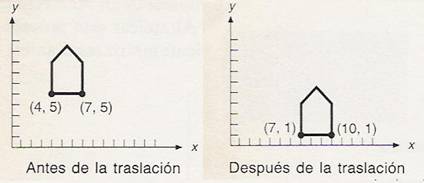
Translación
x’ = x + dx
y’ = y + dy
Si definimos los vectores
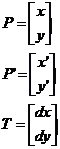
Podemos decir en forma concisa que P’ = P + T . En coordenadas homogéneas podemos
escribir como:
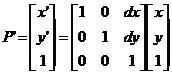
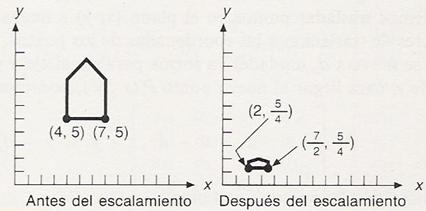
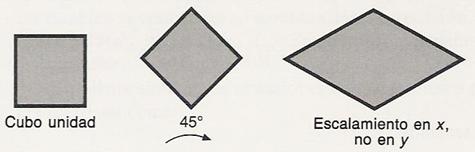
Escalamiento
Para el escalamiento podemos hacer
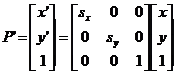
donde sx representa el
factor de escalamiento en x y sy el
factor de escalamiento en y.
Rotación
Para determinar la rotación consideremos un punto
que se encuentra a una distancia del origen R
y esta distancia forma un ángulo f con la horizontal.
x = r cos f
y = r sen f
Si movemos este punto un ángulo q tenemos que
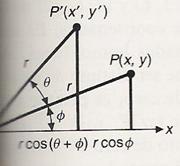
x’ = r cos (f+q) = [r cos f]
cos q
- [rsen f]sen q
y’ = r sen (f+q) = [r cos f]
sen q
- [rsen f]cos q
Lo cual da como resultado que la matriz de rotación
para un punto esta dada por
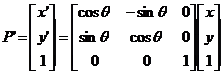
Sesgo
Existe dos posibilidades de hacer transformaciones
de sesgo, la primera en la dirección x y la segunda en la dirección y. Para
aplicar una transformación de sesgo en la dirección x hacemos
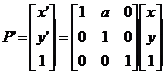
y en la dirección y hacemos
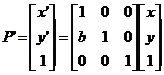
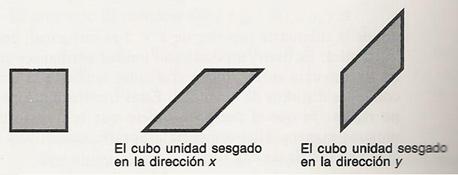
Transformación ventana-área de vista
Consideremos que tenemos una ventana del mundo real
cuyos límites son {x_min, x_max,
y_min, y_max}
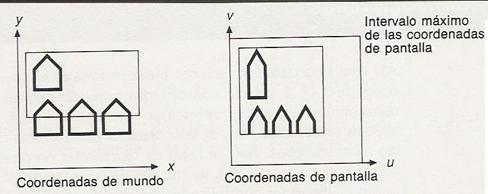
Deseamos mapear a
coordenadas de pantalla con límites {u_min, u_max, v_min, v_max}.
Para tal propósito debemos :
1.- Trasladar las coordenadas mínimas al origen T(-x_min, -y_min),
2.- Aplicar un escalamiento anisotrópico
dado por S((u_max-u_min)/(x_max-x_min),
(v_max-v_min)/(y_max-y_min)) y
3.- Trasladar las coordenadas a un nuevo origen u_min, v_min T(u_min, v_min)
Estos pasos dan la siguiente transformación

Al multiplicar P = M[x,y,1]T se obtiene
![]()
Representación de transformaciones tridimensionales
La translación, escalamiento, rotación y sesgo en
tres dimensiones, es simplemente una extensión de la que se lleva a cabo en dos
dimensiones. Desde este punto de vista podemos representar:
Translación
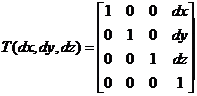
Escalamiento
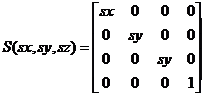
Rotación
Podemos componer rotaciones tridimensionales a
partir de las tres matrices de rotación bidimensional sobre cada uno de los
ejes x, y, y z.
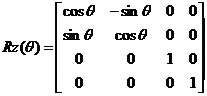
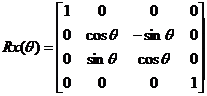
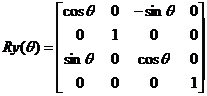
Sesgo
Existen tres matrices de sesgo tridimensional
correspondientes a las matrices de sesgo bidimensional. El sesgo (x,y) es
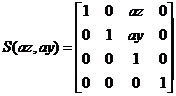
Composición de transformaciones tridimensionales
Podemos
descomponer una transformación tridimensional en
M =
SRT
Componer
una matriz de translación y escalamiento resulta fácil, pero no es el caso de
la matriz de rotación. Para la rotación debemos analizar las propiedades de
esta
Para
el caso de la matriz R tiene la forma
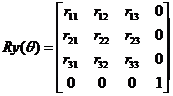
podemos mostrar que:
1.-
Cada vector ri, tiene magnitud
unitaria
2.-
Cada uno es perpendicular al otro riT rj=0
3.-
La inversa de la matriz es la matriz transpuesta
4.-
El determinante de la matriz de rotación es 1.
Ejemplo
Consideremos
el caso de calcular la transformación, para llevar los puntos P1 =[2,1,0]T,
P2 =[4,2,0]T y P3 = [2,3,0]T (definidos en el plano xy) de la posición original a la posición destino (en el
plano zy).
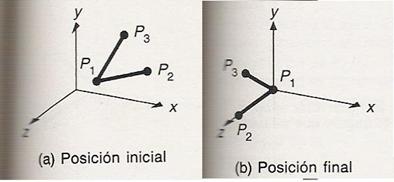
Paso 1.
Calculamos la translación al origen T(-x1, -y1, -z1)
Paso 2.
Calculamos la matriz de rotación
![]()
donde
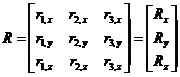
a)
Rz es el vector unitario sobre el vector que va de P1
a P2, P1P2
![]()
b) Rx es el vector perpendicular
al plano definido por P1, P2 y P3
![]()
c) Finalmente
![]()
Para los datos dados
El vector unitario en la dirección P1P2 = [0.894427,
0.447214, 0.000000] y en la dirección P1P3 = [0.000000, 1.000000, 0.000000]
a) Rz = [0.894427,
0.447214, 0.000000]
b) Rx = [0.000000,
0.000000, -1.000000]
c) Ry = Rz x Rx = [-0.447214, 0.894427,
0.000000]
La matriz de transformación queda constituida por
| 0.000000 0.000000
-1.000000 -2.0000|
|-0.447214 0.894427
0.000000 -1.0000|
| 0.894427 0.447214
0.000000 0.0000|
| 0.000000 0.000000 0.000000 1.0000|
Para esta transformación los puntos quedan en la
nueva posición
P1’ = [0.000000 0.000000 0.000000]
P2’ = [0.000000 0.000000
2.236068]
P3’ = [0.000000 1.788854 0.894427]
Podemos hacer un cambio a cualquier plano
simplemente intercambiado los vectores Rx, Ry y Rz. Asi
por ejemplo
a) Para llevar estos puntos al plano xy tenemos
| 0.894427 0.447214
0.000000 -2.00000 |
|-0.447214 0.894427
0.000000 -1.00000 |
| 0.000000 0.000000
-1.000000 0.00000 |
P1’ = [0.000000 0.000000 0.000000]
P2’ = [2.236068 0.000000 0.000000]
P3’ = [0.894427 1.788854 0.000000]
b) Para llevar estos puntos al plano xz tenemos
|
0.894427 0.447214
0.000000 -2.0000 |
|
0.000000 0.000000 -1.000000 -1.0000 |
|-0.447214
0.894427 0.000000 0.0000 |
|
0.000000 0.000000 0.000000 1.0000 |
P1’
= [0.000000 0.000000 0.000000]
P2’
= [2.236068 0.000000 0.000000]
P3’
= [0.894427 0.000000 1.788854]
Ejemplo
Calcular la transformación para llevar puntos en el
plano xy a cualquier plano definido por tres puntos
P1 = [10, 40, 50]T, P2 = [40, 30, 60]T
y P3 = [60, 70, 80]T tomando como referencia el punto 1.
1.- Calculamos el vector unitario en la dirección Rx = P1P2
2.- Calculamos el vector perpendicular al plano Rz = P1P3 x P1P2
3.- Calculamos el vector Ry
= Rz x Rx
De acuerdo con lo anterior esto proyecta el plano
P1-P2-P3 al plano xy, para hacer la operación
calculamos la inversa (la transpuesta es equivalente) con lo cual nuestra
transformación queda:
R = [RxT RyT RzT]
y la transformación final es
M = | R P1T |
| 0 1 |
T = | 0.904534 -0.191460 0.381000
10.000000 |
|-0.301511
-0.919007 0.254000 40.000000 |
| 0.301511
-0.344628 -0.889001 50.000000 |
|
0.000000 0.000000 0.000000 1.000000 |
Ver código ejemplo113.cpp
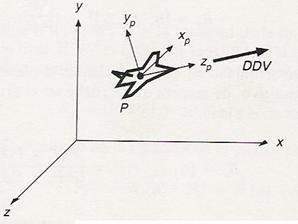
Ejemplo
Considere un aeroplano definido en el sistema
coordenado xp, yp, zp y centrado en el origen. Queremos mover el avión para
que apunte en la dirección del vector unitario de vuelo DDV.
Para resolver
1.- El eje zp debe
transformarse en la dirección de vuelo DDV,
2.- mientras xp es una
dirección perpendicular a DDV o sea y x DDV (y es un vector unitario en la
dirección de y) y
3.- la dirección final yp
debe ser ortogonal al plano zp y xp
así que calculamos esta dirección como DDV x (y x DDV)
La transformación resultante es
| 0 |
T = | y X DDV
DDV X (y X DDV) DDV 0 |
| 0 |
| 0
0
0 1 |