Recursividad
Un método recursivo es un método que se llama a
si mismo directa o indirectamente o a través de otro método. Un ejemplo
interesante de recursion es la función factorial. La definición de factorial
esta dada por el producto:
n! = n*(n-1)*(n-2)*…*3*2*1
Note que esta definición la podemos escribir de
manera recursiva como:
n! = n*(n-1)!
Este método lo podemos escribir en JAVA como:
class
factorial
{
static public void main(String args[])
{
for(int i=0; i<10; i++)
System.out.println(i+"! = " +
factorial (i));
}
static public double factorial(int N)
{
if(N == 0) return 1;
else return (N*factorial(N-1));
}
}
Otro ejemplo de definición recursiva es la
multiplicación de números naturales. El producto a*b, donde a y b son enteros
positivos, puede definirse
class multiplica
{
static public void main(String
args[])
{
int x=4, y=5;
System.out.println(multiplica(4,5));
}
static public double
multiplica(int x, int y)
{
if(y == 1) return x;
else
return (x + multiplica(x,y-1));
}
}
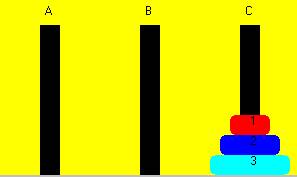
El ejemplo más conocido, de recursividad entre
los programadores, es el problema de las torres de Hanoi. Para este juego, se
tienen tres postes (A, B, C) y un conjunto n de discos colocados de mayor a
menor diámetro en alguno de los postes, por ejemplo el poste A. La meta es
mover todos los discos del poste A al poste C con las siguientes restricciones:
en cada movimiento solo se puede tomar un disco y colocarlo en cualquier poste
y no se debe colocar, un en un poste, un disco de diámetro mayor sobre un
disco de diámetro menor (ejemplo).
La implementación en Java queda de la siguiente
manera
public class ej051 {
public static
void main(String[] args)
{
mover("A", "C", "B", 3);
}
public static
void mover(String a, String b, String c, int n)
{
if (n >
0) {
mover(a,
c, b, n - 1);
System.out.println("Mover un disco del poste
" + a + " al poste " + c);
mover(b, a, c, n - 1);
}
}
}
La solución con tres discos es:
Mover un disco del poste A al poste B
Mover un disco del poste A al poste C
Mover un disco del poste B al poste C
Mover un disco del poste A al poste B
Mover un disco del poste C al poste A
Mover un disco del poste C al poste B
Mover un disco del poste A al poste B