Introducción

OpenGL es una librería grafica de bajo nivel. OpenGL hace disponible al programado un conjunto de primitivas geométricas como puntos líneas polígonos, Imágenes y bitmaps. OpenGL provee un conjunto de comandos que permiten la especificación de objetos geométricos en dos y tres dimensiones, usando las primitivas provistas, junto con los comandos que controlan como estos objetos se dibujan en el marco de la memoria

La API de OpenGL fue diseñada para ser usada con los lenguajes de programación C y C++, pero están siendo construidas para otro numero de lenguajes de programación como Java, Tcl Ada y Fortran.

Las especificaciones de OpenGL se encuentran el la página de Silicon Graphics. Así mismo se han desarrollado muchos tutoriales que se encuentran disponibles en Internet.

Los archivos necesarios para poner en funcionamientos las librerías de OpenGL son

1.- Glut.h

2.- Glut32.lib

3.- Glut32.dll

Las cuales se encuentran disponible en la página ¿?. Si se utiliza Visual C++ estas deben ser ubicadas en los directorios

1.- C:\Archivos de programa\DevStudio\VC\include\gl

2.- C:\Archivos de programa\DevStudio\VC\lib

3.- C:\WINDOWS\SYSTEM32

respectivamente o en lugar adecuado de acuerdo con el compilador de C que se este manejando

Un ejemplo de OpenGL

A continuación se presenta un ejemplo de OpenGL para la creación de una ventana. Este ejemplo es nombrado como ejemplo101.cpp

// Un ejemplo simple de creacion de ventana

// ejemplo101.cpp

#include <windows.h>

#include <gl/glut.h>

// Llamado a la funcion que dibuja la pantalla

void dibuja(void)

{

// Limpia la ventana con el color actual de limpiado

glClear(GL_COLOR_BUFFER_BIT);

// Ejecuta los comando de dibujo

glFlush();

}

// parametros iniciales

void parametros_iniciales(void)

{

glClearColor(0.0f, 0.0f, 1.0f, 1.0f);

}

// Programa principal

void main(void)

{

glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);

glutCreateWindow("Mi primer ejemplo");

glutDisplayFunc(dibuja);

parametros_iniciales();

glutMainLoop();

}

El resultado de la ejecución se muestra en la siguiente figura

ejemplo101.cpp

Algoritmo de Bresenham

Discretización de Líneas

Consideremos una línea recta que pasa por dos puntos P1=[20, 20] y [25,20]. Podemos calcular la línea recta que pasa por estos puntos como

(y-y1) = (y2-y1)*(x-x1)/(x2-x1)

Sustituyendo los valores tenemos

(y-20) = (21-20)*(x-20)/(25-20)

Finalmente tenemos

y = 0.2 x + 16

Podemos calcular los valores utilizando el siguiente código

void linea(int x0, int y0, int x1, int y1)

{

int x;

float dy, dx, y, m;

dy = y1 - y0;

dx = x1 - x0;

m = dy/dx;

y = y0;

for(x = x0; x <= x1; x++)

{

escribir_pixel(x, (int) floor(y+0.5) );

y +=m;

}

Note que se suma 0.5 y se calcula la parte entera para redondear la solución.

Los resultados de este código son

x	y	int(y)
20	20.0	20
21	20.2	20
22	20.4	20
23	20.6	21
24	20.8	21

Si escribimos esta ecuación como F(x,y) = 0.2x – y + 16 podemos notar que cualquier punto:

1.- en la línea siempre dará cero. Por ejemplo F(23, 20.6) = 0

2.- sobre la línea dará un número positivo. Por ejemplo F(23, 22) = -1.4 y

3.- bajo la línea dará un número negativo. Por ejemplo F(23, 20) = 0.6.

Esta representación tiene el problema de utilizar aritmética flotante y no tiene solución en el caso de tener una pendiente infinita. Una manera de lidiar con estos problemas es el algoritmo de Bresenham.

Digamos que queremos dibujar una línea entre dos puntos. Consideremos que la pendiente es m y 0<m<1 y que x1 < x2 y y1 < y2.

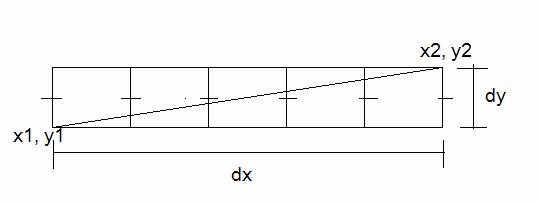
La ecuación de la línea recta la podemos escribir como

y = (dy/dx) x + b

o bien

dx y = dy x + b dx

0 = dy x – dx y + b dx

Multiplicando la ecuación por dos tenemos una función F(x,y) dada como:

F(x,y) = 2*dy*x – 2*dx*y + 2*b*dx

Podemos observar que si tenemos un punto arriba de la línea recta y = mx+b, la función F(x,y) dará valores negativos y en caso contrario números positivos. Para trazar nuestra línea recta nuestros movimientos posibles para x son x = x1, x1+1, x1+2, ..., x2, Así que el primer paso que daremos será [x1+1, y1+1/2], la cual es la línea de punto medio F(x1+1, y1+1/2) a la cual denominaremos d_o

d_o = F(x1+1,y1+1/2) = 2*dy*(x1+1) – 2*dx*(y1+1/2) + 2*b*dx

d_o = 2*dy – dx + 2*dy*x1 – 2*dx*y1 + 2*b*dx

d_o = 2*dy – dx + F(x1, y1)

d_o = 2*dy – dx

Esta función F(x1+Dx, y1+1/2+Dy), evalúa la línea recta de punto medio y es deseable que los valores que demos a Dx y Dy den como resultado puntos [x,y] por debajo de esta. De la figura podemos observar, que los posible movimientos que podemos hacer es hacia el Este (incrementando x en uno) y hacia el Noreste (incrementando x y y en uno). En ambos casos debemos si nuestro punto se encuentra por arriba o por debajo de un punto medio. Estos movimientos son

1.- hacia el este

F_E(x+2,y+1/2) = 2*dy*(x+2) – 2*dx*(y+1/2) + 2*b*dx

= 2*dy* + [2*dy*(x+1) – 2*dx*(y+1/2) + 2*b*dx]

F_E(x+2,y+1/2) = 2*dy + d₀

2.-Hacia el Noroeste

F_NE(x+2,y+3/2) = 2*dy*(x+2) – 2*dx*(y+3/2) + 2*b*dx

= 2*dy* - 2*dx + + d₀

El algoritmo es:

1.- Calcular el valor inicial d₀ y hacer d = d₀, incE = 2*dy y incNE = 2*dy – 2*dx

2.- Para x = x1 hasta x2 con incrementos unitarios

Si d <=0 d = d + incE;

sino hacemos d = d + incNE y también y = y +1

Ejemplo

Dado los puntos P1 = [20, 20] y P2 = [25, 21], calcular la línea recta utilizando el algoritmo de Breseham.

dx = 5

dy = 1

do = 2*dy – dx = -3

incE = 2

incNE = -8

x	y	d	inc	dnva	ynva
20	20	-3	2	-1	20
21	20	-1	2	1	20
22	20	1	-8	-7	21
23	21	-7	2	-5	21
24	21	-5	2	-3	21
25	21	-3	2	-1	21

En el caso de tener dos puntos P1 =[x1, y1] y P2 = [x2, y2] y

- si la pendiente es mayor que 1 entonces los valores de x deben ser tomados como los de y y viceversa.

- si x1 > x2 los puntos P1 y P2 deben ser intercambiados

- si y1 > y2 se deben manejar incrementos de y negativos

Ejemplo

Dado los puntos P1 = [25, 5] y P2 = [20, 20] calcular la línea media.

- Dado que |dy| > |dx| intercambiamos los valores de x por los de y; P1 = [5, 25] y P2 = [20,20]

- Dado que dy es negativo debemos tener decrementos de y y dy = -dy

Con esto tenemos que

dx = 15

dy = -(20 – 25) = 5 Dy = -1

do = 2*dy – dx = 2*5 - 15 = -5

incE = 2*dy = 2*(5) = 10

incNE = 2*(dy-dx) = 2*(5-15) = -20

x->y	y->x	d	inc	dnva	ynva
5	25	-5	10	5	25
6	25	5	-20	-15	24
7	24	-15	10	-5	24
8	24	-5	10	5	24
9	24	5	-20	-15	23
10	23	-15	10	-5	23
11	23	-5	10	5	23
12	23	5	-20	-15	22
13	22	-15	10	-5	22
14	22	-5	10	5	22
15	22	5	-20	-15	21
16	21	-15	10	-5	21
17	21	-5	10	5	21
18	21	5	-20	-15	20
19	20	-15	10	-5	20
20	20	-5	10	5	20

El algoritmo en C es

void linea2D(int x0, int y0, int x1, int y1)

{

if(abs(y1-y0) > abs(x1-x0)) linea_punto_medio(y0, x0, y1, x1, 1);

else linea_punto_medio(x0, y0, x1, y1, 0);

}

/* *************************************************

Dibuja una linea en 2d utilizando el algoritmo de

Bresenham

************************************************* */

void linea_punto_medio(int x0, int y0, int x1, int y1, int m)

{

int dx, dy, incr_E, incr_NE, d, x, y;

int pendiente;

// Invierte las lineas si x1 es mayor que x2

if(x0 > x1)

{

linea_punto_medio(x1, y1, x0, y0, m);

return;

}

dx = x1 - x0;

dy = y1 - y0;

// Ajusta el incremento en y para pendientes negativas

if(dy <0)

{

pendiente = -1;

dy = -dy;

}

else

pendiente = 1;

d = dy * 2 - dx;

incr_E = dy*2;

incr_NE = (dy - dx)*2;

printf("%d %d %d \n", d, incr_E, incr_NE);

x = x0;

y = y0;

while(x <= x1)

{

if(m == 0)

{

escribir_pixel(x, y);

printf("%d %d %d ", x, y, d);

}

else

{

escribir_pixel(y, x);

printf("%d %d %d ", y, x, d);

}

if(d <=0) {

d += incr_E;

x++;

printf("%d %d %d\n", incr_E, d, y);

}

else {

d += incr_NE;

x++;

y+= pendiente;

printf("%d %d %d\n", incr_NE, d, y);

}

En tres dimensiones el algoritmo de Bresenham queda como

void linea_punto_medio(int x1, int y1, int z1, int x2, int y2, int z2)

{

int i, dx, dy, dz, l, m, n, x_inc, y_inc, z_inc, err_1, err_2, dx2, dy2, dz2;

int pixel[3];

pixel[0] = x1;

pixel[1] = y1;

pixel[2] = z1;

dx = x2 - x1;

dy = y2 - y1;

dz = z2 - z1;

x_inc = (dx < 0) ? -1 : 1;

l = abs(dx);

y_inc = (dy < 0) ? -1 : 1;

m = abs(dy);

z_inc = (dz < 0) ? -1 : 1;

n = abs(dz);

dx2 = l << 1;

dy2 = m << 1;

dz2 = n << 1;

if ((l >= m) && (l >= n)) {

err_1 = dy2 - l;

err_2 = dz2 - l;

for (i = 0; i < l; i++) {

PUT_PIXEL(pixel);

if (err_1 > 0) {

pixel[1] += y_inc;

err_1 -= dx2;

}

if (err_2 > 0) {

pixel[2] += z_inc;

err_2 -= dx2;

}

err_1 += dy2;

err_2 += dz2;

pixel[0] += x_inc;

}

} else if ((m >= l) && (m >= n)) {

err_1 = dx2 - m;

err_2 = dz2 - m;

for (i = 0; i < m; i++) {

PUT_PIXEL(pixel);

if (err_1 > 0) {

pixel[0] += x_inc;

err_1 -= dy2;

}

if (err_2 > 0) {

pixel[2] += z_inc;

err_2 -= dy2;

}

err_1 += dx2;

err_2 += dz2;

pixel[1] += y_inc;

}

} else {

err_1 = dy2 - n;

err_2 = dx2 - n;

for (i = 0; i < n; i++) {

PUT_PIXEL(pixel);

if (err_1 > 0) {

pixel[1] += y_inc;

err_1 -= dz2;

}

if (err_2 > 0) {

pixel[0] += x_inc;

err_2 -= dz2;

}

err_1 += dy2;

err_2 += dx2;

pixel[2] += z_inc;

}

PUT_PIXEL(pixel);

}

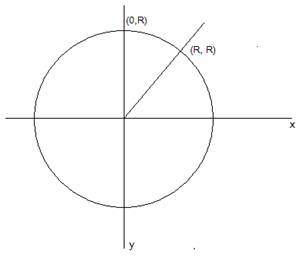
Algoritmo de Círculo de punto medio

Consideraremos sólo 45º de un círculo, el segundo octante de x=0 a x = y = R, podemos calcular los puntos restantes utilizando simetría así:

void puntos_circulo(float x, float y)

{

escribir_pixel(x, y);

escribir_pixel(y, x);

escribir_pixel(y, -x);

escribir_pixel(x, -y);

escribir_pixel(-x, -y);

escribir_pixel(-y, -x);

escribir_pixel(-y, x);

escribir_pixel(-x, y);

}

Para el trazado de los puntos en este octante de 45 grados, definimos F(x,y) = x² + y² – R²; esta función es cero en el círculo, positiva fuera del circulo y negativo dentro de el. Podemos ver que si el punto medio entre los puntos E y SE está fuera del circulo, entonces el píxel SE es el más cercano al circulo. Por otra parte, si el punto medio está dentro del círculo, el píxel E es el más cercano.

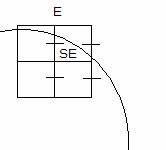
Como se hizo con las líneas, la elección se basa en la variable de decisión d, la cual constituye el valor de la función en el punto medio

d_viejo = F(x1+1, y1-1/2) = (x1+1)² + (y1-1/2)² – R²

d_viejo = (x12 + y12 – R²) + 2x1 + 1 + y1 + 1/4

d_viejo = 2x1 - y1 + 5/4

en el punto inicial (0, R)

d_viejo = 2x1 - y1 + 5/4 = 5/4 - R

Si d_viejo < 0 se escoge E y el siguiente punto medio será un incremento en x. Entonces

d_nuevo = F(x1+2, y1-1/2) = x1² + 2x1 +4 + (y1-1/2)² – R²

d_nuevo = (x1+1)² + (y1-1/2)² – R²+2x1 + 3

d_nuevo = d_viejo+ 2x1 + 3

Si dviejo >= 0, se elige SE y el siguiente punto medio será un incremento en x y un decremento en y. Entonces

d_nuevo = F(x1+2, y1-3/2) = x1² + 2x1 +4 + y1² – 3y1 + 9/4 – R²

d_nuevo = (x1+1)² + (y1-1/2)² – R²+(2x1 + 3) + (-2y1 + 2)

d_nuevo = d_viejo+ 2x1 – 2y1 + 5

Ejemplo.

Realizar el trazado, utilizando el algoritmo de Bresenham de un círculo de radio 5.

El punto inicial x1 = 0 y y1 = 5

inc_E = 2x1 + 3 = 2*0 + 3 = 3

inc_SE = 2x1 – 2y1 + 5 = 2*0 – 2*5 + 5 = -5

d_o = 5/4 – 5 = -15/4

x	y	d	inc	d_nva	x_nva	y_nva
0	5	-3.75	3	-0.75	1	5
1	5	-0.75	6	4.25	2	5
2	5	4.25	-1	3.25	3	4
3	4	3.25	3	6.25	4	3

El código en C queda como:

void circulo_punto_medio(int radio)

{

int x, y;

float d;

x = 0;

y = radio;

d = 5.0/4.0-radio;

puntos_circulo(x, y);

while(y > x)

{

if(d < 0) {

d += x*2 + 3;

x++;

}

else {

d += (x - y)*2 + 5;

x++;

y--;

}

puntos_circulo(x,y);

}

Rellenado de Rectángulos

La discretización de un rectángulo no es más que dos ciclos anidados, siempre y cuando la base y la altura sean paralelos a los ejes x y y.

for(int y = ymin; y <= ymax; y++)

for(int x = xmin; x <= xmax; x++)

escribir_pixel(x,y);

Rellenado de Polígonos

Dado un conjunto de puntos que forman un polígono creamos la Lista Global de Aristas LGA. Hay que recordar que una arista esta formada por dos puntos P_i y P_i+1. Nuestra LGA tendrá la siguiente información.

1.- ymin el cual es el valor mínimo entre y_i y y_i+1

2.- ymax el cual es el valor máximo entre y_i y y_i+1

3.- xval es el valor de la xi correspondiente a la y mínima:

es decir xval

if(y_i < y_i+1) return x_i

else return x_i+1

4.- Calculamos la pendiente 1/m como (x_i – x_i+1)/(y_i – y_i+1)

Una vez creada la LGA, el algoritmo para rellenado de polígonos es:

1.- Hacer y igual a la menor coordenada ymin de la LGA

2.- Crear una Lista de Aristas Activas LAA que inicialmente este vacía

3.- Repetir el procedimiento mientras TAA y TA no estén vacías

3.1 mover de la LGA a la LAA las aristas con ymin = y y luego ordenar LAA con base a la coordenada x.

3.2 Rellenar los valores de los píxeles deseados en la línea de rastreo y usando pares de coordenadas x de LAA.

3.3 Eliminar de la LAA las entradas con y = ymax

3.4 incrementar y en 1

3.5 Actualizar x para la nueva y en cada arista no vertical que pertenezca a la LAA haciendo

x^(k+1) = x^(k) + 1/m

Ejemplo del Pescadito

Dado los siguientes vértices rellenar el polígono correspondiente

x y

10, 10

10, 16

16, 20

28, 10

28, 16

22, 10

Creamos la LGA

n	ymin	ymax	xval	1/m
1	10	16	10	0.0
2	16	20	10	1.5
3	10	20	28	-1.2
4	10	16	28	0
5	10	16	22	1
6	10	10	10	inf

Nota: la arista 6 es borrada ya que su pendiente es infinita

Paso 1

y = 10 [10, 20]

Paso 2

LA =

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 16.000000 22.000000 1.000000

10.000000 16.000000 28.000000 0.000000

10.000000 20.000000 28.000000 -1.200000

-------------------------------------------

LAG

-------------------------------------------

16.000000 20.000000 10.000000 1.500000

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 16.000000 22.000000 1.000000

10.000000 16.000000 28.000000 0.000000

10.000000 20.000000 28.000000 -1.200000

-------------------------------------------

Paso 3.2

x = {10 11 12 13 14 15 16 17 18 19 20 21 22 28}

Paso 3.4 incrementa y=11

Paso 3.5 LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 16.000000 23.000000 1.000000

10.000000 16.000000 28.000000 0.000000

10.000000 20.000000 26.799999 -1.200000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 16.000000 23.000000 1.000000

10.000000 20.000000 26.799999 -1.200000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

LAG

-------------------------------------------

16.000000 20.000000 10.000000 1.500000

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 16.000000 23.000000 1.000000

10.000000 20.000000 26.799999 -1.200000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

Paso 3.2

x = {10 11 12 13 14 15 16 17 18 19 20 21 22 23 27 28}

Paso 3.4 incrementa y=12

Paso 3.5 LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 16.000000 24.000000 1.000000

10.000000 20.000000 25.599998 -1.200000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 16.000000 24.000000 1.000000

10.000000 20.000000 25.599998 -1.200000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

LAG

-------------------------------------------

16.000000 20.000000 10.000000 1.500000

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 16.000000 24.000000 1.000000

10.000000 20.000000 25.599998 -1.200000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

Paso 3.2

x = {10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 26 27 28}

Paso 3.4 incrementa y=13

Paso 3.5 LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 16.000000 25.000000 1.000000

10.000000 20.000000 24.399998 -1.200000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 20.000000 24.399998 -1.200000

10.000000 16.000000 25.000000 1.000000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

LAG

-------------------------------------------

16.000000 20.000000 10.000000 1.500000

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 20.000000 24.399998 -1.200000

10.000000 16.000000 25.000000 1.000000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

Paso 3.2

x = {10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28}

Paso 3.4 incrementa y=14

Paso 3.5 LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 20.000000 23.199997 -1.200000

10.000000 16.000000 26.000000 1.000000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 20.000000 23.199997 -1.200000

10.000000 16.000000 26.000000 1.000000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

LAG

-------------------------------------------

16.000000 20.000000 10.000000 1.500000

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 20.000000 23.199997 -1.200000

10.000000 16.000000 26.000000 1.000000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

Paso 3.2

x = {10 11 12 13 14 15 16 17 18 19 20 21 22 23 26 27 28}

Paso 3.4 incrementa y=15

Paso 3.5 LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 20.000000 21.999996 -1.200000

10.000000 16.000000 27.000000 1.000000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 20.000000 21.999996 -1.200000

10.000000 16.000000 27.000000 1.000000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

LAG

-------------------------------------------

16.000000 20.000000 10.000000 1.500000

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 20.000000 21.999996 -1.200000

10.000000 16.000000 27.000000 1.000000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

Paso 3.2

x = {10 11 12 13 14 15 16 17 18 19 20 21 22 27 28}

Paso 3.4 incrementa y=16

Paso 3.5 LAA

-------------------------------------------

10.000000 16.000000 10.000000 0.000000

10.000000 20.000000 20.799995 -1.200000

10.000000 16.000000 28.000000 1.000000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

16.000000 20.000000 10.000000 1.500000

10.000000 16.000000 10.000000 0.000000

10.000000 20.000000 20.799995 -1.200000

10.000000 16.000000 28.000000 1.000000

10.000000 16.000000 28.000000 0.000000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

16.000000 20.000000 10.000000 1.500000

10.000000 20.000000 20.799995 -1.200000

-------------------------------------------

Paso 3.2

x = {10 11 12 13 14 15 16 17 18 19 20 21}

Paso 3.4 incrementa y=17

Paso 3.5 LAA

-------------------------------------------

16.000000 20.000000 11.500000 1.500000

10.000000 20.000000 19.599995 -1.200000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

16.000000 20.000000 11.500000 1.500000

10.000000 20.000000 19.599995 -1.200000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

16.000000 20.000000 11.500000 1.500000

10.000000 20.000000 19.599995 -1.200000

-------------------------------------------

Paso 3.2

x = {12 13 14 15 16 17 18 19 20}

Paso 3.4 incrementa y=18

Paso 3.5 LAA

-------------------------------------------

16.000000 20.000000 13.000000 1.500000

10.000000 20.000000 18.399994 -1.200000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

16.000000 20.000000 13.000000 1.500000

10.000000 20.000000 18.399994 -1.200000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

16.000000 20.000000 13.000000 1.500000

10.000000 20.000000 18.399994 -1.200000

-------------------------------------------

Paso 3.2

x = {13 14 15 16 17 18}

Paso 3.4 incrementa y=19

Paso 3.5 LAA

-------------------------------------------

16.000000 20.000000 14.500000 1.500000

10.000000 20.000000 17.199993 -1.200000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

16.000000 20.000000 14.500000 1.500000

10.000000 20.000000 17.199993 -1.200000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

16.000000 20.000000 14.500000 1.500000

10.000000 20.000000 17.199993 -1.200000

-------------------------------------------

Paso 3.2

x = {15 16 17}

Paso 3.4 incrementa y=20

Paso 3.5 LAA

-------------------------------------------

16.000000 20.000000 16.000000 1.500000

10.000000 20.000000 15.999993 -1.200000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

10.000000 20.000000 15.999993 -1.200000

16.000000 20.000000 16.000000 1.500000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

Paso 3.2

{}

Paso 3.4 incrementa y=21

Paso 3.5 LAA

-------------------------------------------

El resultado es tal como se muestra enseguida.

***

******

*********

************

************* **

************** ***

*******************

*************** ***

************** **

************* *

Ejemplo de un polígono

Dados los vértices

x y

2, 3

2, 9

7, 7

13, 11

13, 5

7, 2

La Lista Global de aristas queda:

n	ymin	ymax	xval	1/m
1	3	9	2	0.0
2	7	9	7	-2.5
3	7	11	7	1.5
4	5	11	13	0
5	2	5	7	-5
6	2	3	7	2

Paso 1

y = 2 [2, 11]

Paso 2

LA =

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

2.000000 3.000000 7.000000 -5.000000

2.000000 5.000000 7.000000 2.000000

-------------------------------------------

LAG

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

7.000000 9.000000 7.000000 -2.500000

7.000000 11.000000 7.000000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

2.000000 3.000000 7.000000 -5.000000

2.000000 5.000000 7.000000 2.000000

-------------------------------------------

Paso 3.2

x ={7 }

Paso 3.4 incrementa y=3

Paso 3.5 LAA

-------------------------------------------

2.000000 3.000000 2.000000 -5.000000

2.000000 5.000000 9.000000 2.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

2.000000 3.000000 2.000000 -5.000000

2.000000 5.000000 9.000000 2.000000

-------------------------------------------

LAG

-------------------------------------------

7.000000 9.000000 7.000000 -2.500000

7.000000 11.000000 7.000000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

2.000000 5.000000 9.000000 2.000000

-------------------------------------------

Paso 3.2

x ={2 3 4 5 6 7 8 9 }

Paso 3.4 incrementa y=4

Paso 3.5 LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

2.000000 5.000000 11.000000 2.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

2.000000 5.000000 11.000000 2.000000

-------------------------------------------

LAG

-------------------------------------------

7.000000 9.000000 7.000000 -2.500000

7.000000 11.000000 7.000000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

2.000000 5.000000 11.000000 2.000000

-------------------------------------------

Paso 3.2

x ={2 3 4 5 6 7 8 9 10 11 }

Paso 3.4 incrementa y=5

Paso 3.5 LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

2.000000 5.000000 13.000000 2.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

5.000000 11.000000 13.000000 0.000000

2.000000 5.000000 13.000000 2.000000

-------------------------------------------

LAG

-------------------------------------------

7.000000 9.000000 7.000000 -2.500000

7.000000 11.000000 7.000000 1.500000

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.2

x ={2 3 4 5 6 7 8 9 10 11 12 13 }

Paso 3.4 incrementa y=6

Paso 3.5 LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

LAG

-------------------------------------------

7.000000 9.000000 7.000000 -2.500000

7.000000 11.000000 7.000000 1.500000

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.2

x ={2 3 4 5 6 7 8 9 10 11 12 13 }

Paso 3.4 incrementa y=7

Paso 3.5 LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

7.000000 11.000000 7.000000 1.500000

7.000000 9.000000 7.000000 -2.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

7.000000 11.000000 7.000000 1.500000

7.000000 9.000000 7.000000 -2.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.2

x ={2 3 4 5 6 7 }

7 8 9 10 11 12 13 }

Paso 3.4 incrementa y=8

Paso 3.5 LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

7.000000 11.000000 8.500000 1.500000

7.000000 9.000000 4.500000 -2.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

7.000000 9.000000 4.500000 -2.500000

7.000000 11.000000 8.500000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

7.000000 9.000000 4.500000 -2.500000

7.000000 11.000000 8.500000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.2

x ={2 3 4 5 }

9 10 11 12 13 }

Paso 3.4 incrementa y=9

Paso 3.5 LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

7.000000 9.000000 2.000000 -2.500000

7.000000 11.000000 10.000000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

3.000000 9.000000 2.000000 0.000000

7.000000 9.000000 2.000000 -2.500000

7.000000 11.000000 10.000000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

7.000000 11.000000 10.000000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.2

x ={10 11 12 13 }

Paso 3.4 incrementa y=10

Paso 3.5 LAA

-------------------------------------------

7.000000 11.000000 11.500000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

7.000000 11.000000 11.500000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

7.000000 11.000000 11.500000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.2

x ={12 13 }

Paso 3.4 incrementa y=11

Paso 3.5 LAA

-------------------------------------------

7.000000 11.000000 13.000000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

7.000000 11.000000 13.000000 1.500000

5.000000 11.000000 13.000000 0.000000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

Paso 3.2

x ={}

Paso 3.4 incrementa y=12

Paso 3.5 LAA

-------------------------------------------

****

**** *****

************

**********

********

Ejemplo del triangulito

Las coordenadas de los vértices para este polígono son:

x y

2, 2

20, 2

9, 10

La Lista global de aristas es

n	ymin	ymax	xval	1/m
1	2	2	2	inf
2	2	10	20	-1.375
3	2	10	2	0.875

Paso 1

y = 2 [2, 10]

Paso 2

LA =

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

2.000000 10.000000 2.000000 0.875000

2.000000 10.000000 20.000000 -1.375000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

2.000000 10.000000 2.000000 0.875000

2.000000 10.000000 20.000000 -1.375000

-------------------------------------------

Paso 3.2

x ={2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 }

Paso 3.4 incrementa y=3

Paso 3.5 LAA

-------------------------------------------

2.000000 10.000000 2.875000 0.875000

2.000000 10.000000 18.625000 -1.375000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

2.000000 10.000000 2.875000 0.875000

2.000000 10.000000 18.625000 -1.375000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

2.000000 10.000000 2.875000 0.875000

2.000000 10.000000 18.625000 -1.375000

-------------------------------------------

Paso 3.2

x ={3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 }

Paso 3.4 incrementa y=4

Paso 3.5 LAA

-------------------------------------------

2.000000 10.000000 3.750000 0.875000

2.000000 10.000000 17.250000 -1.375000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

2.000000 10.000000 3.750000 0.875000

2.000000 10.000000 17.250000 -1.375000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

2.000000 10.000000 3.750000 0.875000

2.000000 10.000000 17.250000 -1.375000

-------------------------------------------

Paso 3.2

x ={4 5 6 7 8 9 10 11 12 13 14 15 16 17 }

Paso 3.4 incrementa y=5

Paso 3.5 LAA

-------------------------------------------

2.000000 10.000000 4.625000 0.875000

2.000000 10.000000 15.875000 -1.375000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

2.000000 10.000000 4.625000 0.875000

2.000000 10.000000 15.875000 -1.375000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

2.000000 10.000000 4.625000 0.875000

2.000000 10.000000 15.875000 -1.375000

-------------------------------------------

Paso 3.2

x ={5 6 7 8 9 10 11 12 13 14 15 16 }

Paso 3.4 incrementa y=6

Paso 3.5 LAA

-------------------------------------------

2.000000 10.000000 5.500000 0.875000

2.000000 10.000000 14.500000 -1.375000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

2.000000 10.000000 5.500000 0.875000

2.000000 10.000000 14.500000 -1.375000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

2.000000 10.000000 5.500000 0.875000

2.000000 10.000000 14.500000 -1.375000

-------------------------------------------

Paso 3.2

x ={6 7 8 9 10 11 12 13 14 15 }

Paso 3.4 incrementa y=7

Paso 3.5 LAA

-------------------------------------------

2.000000 10.000000 6.375000 0.875000

2.000000 10.000000 13.125000 -1.375000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

2.000000 10.000000 6.375000 0.875000

2.000000 10.000000 13.125000 -1.375000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

2.000000 10.000000 6.375000 0.875000

2.000000 10.000000 13.125000 -1.375000

-------------------------------------------

Paso 3.2

x ={6 7 8 9 10 11 12 13 }

Paso 3.4 incrementa y=8

Paso 3.5 LAA

-------------------------------------------

2.000000 10.000000 7.250000 0.875000

2.000000 10.000000 11.750000 -1.375000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

2.000000 10.000000 7.250000 0.875000

2.000000 10.000000 11.750000 -1.375000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

2.000000 10.000000 7.250000 0.875000

2.000000 10.000000 11.750000 -1.375000

-------------------------------------------

Paso 3.2

x ={7 8 9 10 11 12 }

Paso 3.4 incrementa y=9

Paso 3.5 LAA

-------------------------------------------

2.000000 10.000000 8.125000 0.875000

2.000000 10.000000 10.375000 -1.375000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

2.000000 10.000000 8.125000 0.875000

2.000000 10.000000 10.375000 -1.375000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

2.000000 10.000000 8.125000 0.875000

2.000000 10.000000 10.375000 -1.375000

-------------------------------------------

Paso 3.2

x ={8 9 10 }

Paso 3.4 incrementa y=10

Paso 3.5 LAA

-------------------------------------------

2.000000 10.000000 9.000000 0.875000

2.000000 10.000000 9.000000 -1.375000

-------------------------------------------

Paso 3.1

LAA

-------------------------------------------

2.000000 10.000000 9.000000 0.875000

2.000000 10.000000 9.000000 -1.375000

-------------------------------------------

LAG

-------------------------------------------

Paso 3.3 LAA

-------------------------------------------

Paso 3.2

x ={}

Paso 3.4 incrementa y=11

Paso 3.5 LAA

-------------------------------------------

El resultado es:

***

******

********

**********

************

**************

*****************

*******************

Recorte de Líneas

Algoritmo de recorte de Cohen-Sutherland

Consideremos que deseamos recortar un conjunto de líneas dentro de un área determinada por los valores en x [x_min, x_max] y en y por los límites [y_min, y_ymax]. Para ello haremos uso de un código de cuatro bits dado por

primer bit	encima de la arista superior	y > y_max
segundo bit	debajo de la arista inferior	y < y_min
tercer bit	a la derecha de la arista derecha	x > x_max
cuarto bit	a la izquierda de la arista izquierda	x < x_min

Este código se aplica tal como se muestra en la siguiente figura

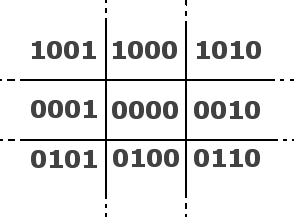
Note que solo las líneas que no interceptan el área de corte tendrán un código 0000. Con tal propósito se crea la estructura

typedef struct {

unsigned todas;

unsigned izquierda: 1;

unsigned derecha: 1;

unsigned inferior: 1;

unsigned superior: 1;

} codigo_region;

La cual es llenada con el llamado a la siguiente función

codigo_region calculo_codigo_region(float x, float y, float xmin, float xmax, float ymin, float ymax)

{

codigo_region codigo;

codigo.todas = 0;

if(y > ymax) {

codigo.superior = 1;

codigo.todas += codigo.superior;

} else if(y < ymin) {

codigo.inferior = 1;

codigo.todas += codigo.inferior;

}

if(x > xmax) {

codigo.derecha = 1;

codigo.todas += codigo.derecha;

} else if(x < xmin) {

codigo.izquierda = 1;

codigo.todas += codigo.izquierda;

}

return codigo;

}

Una vez calculado la intersección con cada una de las aristas de corte, debemos calcular el punto de corte. Así por ejemplo dado los puntos P0 =[x0, y0] y P1 = [x1, y1] debemos considerar los cuatro casos de intersección con el área de corte

Caso I La línea intercepta con la línea superior en el punto P donde la coordenada en y es y_max y la coordenada en x debemos calcular.

x = x0 + (x1 – x0)*(y_max – y0)/(y1 – y0)

Caso II La línea intercepta con la línea inferior en el punto P donde la coordenada en y es y_min y la coordenada en x debemos calcular como

x = x0 + (x1 – x0)*(y_min – y0)/(y1 – y0)

Caso III La línea intercepta con la línea derecha en el punto P donde la coordenada en x es x_max y la coordenada en y debemos calcular como

y = y0 + (y1 – y0)*(x_max – x)/(x1 – x0)

Caso IV La línea intercepta con la línea izquierda en el punto P donde la coordenada en x es x_min y la coordenada en y debemos calcular como

y = y0 + (y1 – y0)*(x_min – x)/(x1 – x0)

void recorte_y_dubujo_de_lineas_Cohen_Sutherland(float x0, float y0, float x1, float y1, float xmin, float xmax, float ymin, float ymax)

{

boolean aceptar, fin;

codigo_region codigo_region0, codigo_region1, codigo_region_salida;

float x, y;

printf("%f %f %f %f\n", x0, y0, x1, y1);

aceptar = FALSE;

fin = FALSE;

codigo_region0 = calculo_codigo_region(x0, y0, xmin, xmax, ymin, ymax);

codigo_region1 = calculo_codigo_region(x1, y1, xmin, xmax, ymin, ymax);

do {

if(codigo_region0.todas == 0 && codigo_region1.todas == 0) {

aceptar = TRUE;

fin = TRUE;

} else if(codigo_region0.todas & codigo_region1.todas!= 0)

fin = TRUE;

else {

if(codigo_region0.todas != 0)

codigo_region_salida = codigo_region0;

else

codigo_region_salida = codigo_region1;

if(codigo_region_salida.superior) {

x = x0 + (x1-x0)*(ymax - y0)/(y1 - y0);

y = ymax;

} else if(codigo_region_salida.inferior) {

x = x0 + (x1 - x0)*(ymin - y0)/(y1 - y0);

y = ymin;

} else if(codigo_region_salida.derecha) {

y = y0 + (y1 - y0) *(xmax - x0)/(x1 - x0);

x = xmax;

} else if(codigo_region_salida.izquierda) {

y = y0 + (y1 - y0)*(xmin - x0)/(x1 - x0);

x = xmin;

}

if(codigo_region_salida.todas == codigo_region0.todas) {

x0 = x;

y0 = y;

codigo_region0 = calculo_codigo_region(x0, y0, xmin, xmax, ymin, ymax);

} else {

x1 = x;

y1 = y;

codigo_region1 = calculo_codigo_region(x1, y1, xmin, xmax, ymin, ymax);

}

} while(!fin);

printf("%f %f %f %f\n", x0, y0, x1, y1);

if(aceptar)

{

printf("%f %f %f %f", x0, y0, x1, y1);

linea2D(x0, y0, x1, y1);

}

Ejemplo

Calcular el recorte correspondiente a las siguientes líneas utilizando el algoritmo de Cohen-Sutherland. Suponga que el área de recorte esta dada en el eje x por [10, 50] y en y por [10, 50]

Línea	origen	destino
1	[0,0]	[100,100]
2	[-100, 10]	[40, 40]
3	[20,70]	[40, 20]
4	[15, 20]	[25, -20]

Aplicando el algoritmo tenemos la siguiente solución

Línea	origen	código	recorte	destino	código	recorte
1	[0,0]	0101	[10,10]	[100,100]	1010	[50,50]
2	[-100, 10]	0001	[10,33.571430]	[40, 40]	0000	[40,40]
3	[20,70]	1000	[28, 50]	[40, 20]	0000	[40,20]
4	[15, 20]	0000	[15,20]	[25, -20]	0100	[17.5, 10]

Algoritmo Paramétrico de recorte de líneas.

El algoritmo de Cyrus-Beck se basa en la siguiente formulación de la intersección entre dos líneas. En la figura se muestra una arista Ei del rectángulo de recorte y la normal exterior de la Ni, así como el segmento de línea de P0 a P1 que debe recortarse en la arista.

La línea la representaremos en forma paramétrica como

P(t) = P0 + t(P1 – P0)

Línea:

P(t) = P₀ + t(P₁ - P₀)

...

x = x₀ + (x₁ - x₀)t

y = y₀ + (y₁ - y₀)t

Intersección [ P(t) ]

N_i ^. [P(t) - P_Ei] = 0

N_i ^. [P₀ + t(P₁ - P₀) - P_Ei] = 0

t = (N_i^.[P₀-P_Ei])/(-N_i^.(P₁-P₀))

= (N_i^.[P₀-P_Ei])/(-N_i^. D)

donde t = 0 en P0 y t = 1 en P1. Elegimos un punto arbitrario PEi en la Arista Ei. La meta es calcular el valor de t, donde la línea interfecta a la arista, en otras palabras

Ni . [P(t)-PEi] = 0

Sustituyendo el valor de P(t) y despejando

Ni . [P0 + t(P1 – P0) - PEi] = 0

t = Ni.[P0 –PEi]/[-Ni.(P1 – P0)]

Cyrus - Beck: Clasificación de las intersecciones

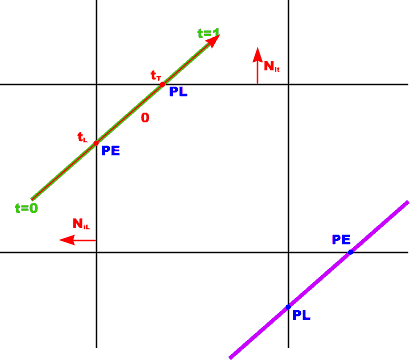
Potentially entering Intersection (PE)

  N_i D < 0 (angle > 90^o) => t_E

Potentially leaving Intersection (PL)

  N_i D > 0 (angle < 90^o) => t_L

El algoritmo en C es

void Recorte_Lineas_Cyrus_Beck(float x0, float y0, float x1, float y1, float xmin, float xmax, float ymin, float ymax)

{

int i;

float N[4][2] = {-1, 0, 0, 1, 1, 0, 0, -1};

float E[4][2], P0[2], P1[2], t, ND, tE=0, tL=1;

float P2[2], P3[2];

E[0][0] = xmin; E[0][1] = (ymax + ymin)/2.0;

E[1][0] = (xmax + xmin)/2.0; E[1][1] = ymax;

E[2][0] = xmax; E[2][1] = (ymax + ymin)/2.0;

E[3][0] = (xmax + xmin)/2.0; E[3][1] = ymin;

P0[0] = x0; P0[1] = y0;

P1[0] = x1; P1[1] = y1;

for(i=0; i<4; i++)

{

tE = 0;

tL = 1;

ND = calcula_ND(P0, P1, N[i]);

if(ND != 0)

{

t = calcula_t(P0, P1, N[i], E[i]);

if(ND <0) tE = MAX(tE, t)

else tL = MIN(tL, t);

}

P2[0] = P0[0] + tE*(P1[0]-P0[0]);

P2[1] = P0[1] + tE*(P1[1]-P0[1]);

P3[0] = P0[0] + tL*(P1[0]-P0[0]);

P3[1] = P0[1] + tL*(P1[1]-P0[1]);

if(tE < tL)

{

P0[0] = P2[0]; P0[1] = P2[1];

P1[0] = P3[0]; P1[1] = P3[1];

}

linea2D(P0[0], P0[1], P1[0], P1[1]);

//printf("Cortes %f %f %f %f\n", P0[0], P0[1], P1[0], P1[1]);

}

Recorte de Polígonos

El algoritmo acepta una serie de vértices de polígonos v1, v2, ..., vn. En dos dimensiones, los vértices definen aristas de polígonos de vi a vi-1 y de vn a v1. El algoritmo recorta con respecto a una sola arista infinita y produce una serie de vértices que define el polígono recortado.

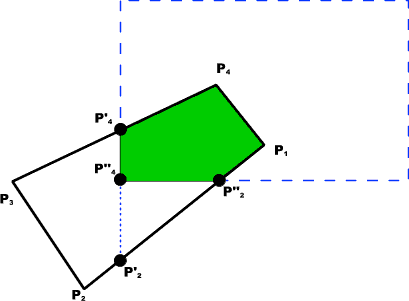
El algoritmo recorre el polígono de vn a v1 y luego de regreso de a vn, examinando en cada paso la relación entre los vértices sucesivos y la arista de recorte. En cada paso se añaden cero, uno o dos vértices a la lista de salida de los vértices que definen el polígono recortado. Es necesario analizar cuatro casos posibles como se ilustra en la figura.

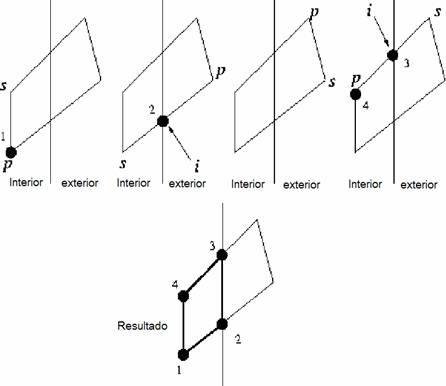
Caso 1: cuando la arista del polígono está completamente dentro de las fronteras de recorte, se agrega el vértice p.

Caso 2: El punto de intersección i se produce como vértice porque la arista interseca la frontera

Caso 3: En este caso ambos vértices se hallan fuera de las fronteras, por lo cual no hay salida

Caso 4: El punto de intersección i y el vértice p se añaden a la lista de salida.

1. Para cada arista, verificar los valores de las arista, s y p. Si ambos valores son:

1. Interior-interior, agregue el Segundo vertice p.

2. Interior-exterior, calcule y agregue la intersección i de la arista sp con la línea de recorte.

3. Exterior-exterior, no hacer ninguna operación.

4. Exterior-interior, calcule y agregue la intersección i de la arista sp con la línea de recorte y agregue también el nodo p.

2. El resultado es la lista ordenada de los vértices del polígono recortado.

Ejemplo.

Dados los puntos

x	y
20	20
35	27
30	30
20	24

Considerando como línea de recorte la dada por los puntos {[25, 20], [25, 40]} y que el polígono esta a la izquierda de la línea.

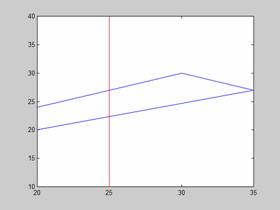
Las arista que tenemos son A1 = {[20, 20], [35, 27]}, A2 = {[35, 27], [30, 30]}, A3 = {[30, 30], [20, 24]} y A4 = {[20, 24], [20, 20]}

Para A1

Tenemos que s=[20, 20], p=[35, 27], caso 2, por lo cual agregamos la intersección

y = (27-20)/(35-20)*(25-20) + 20 = 22.3333

salida = {[25, 22.3333]}

Para A2

Tenemos que s = [35, 27] y p = [30, 30], caso 3, no realizamos ninguna operación

Para A3

Tenemos que s = [30, 30] y p = [20, 24], caso 4, agregamos la intersección y el vértice p

y = (24-30)/(20-30)*(25-30) + 30

salida = {[25, 22.3333], [30, 30], [20, 24]}

Finalmente para la arista A4

Tenemos que s = [20, 24] y p = [20, 20] lo cual nos lleva al caso I, por lo cual agregamos el vértice p

salida = {[20, 20], [25, 22.3333], [30, 30], [20, 24]}

Regresar