Método de Bairstow.
El método de
Bairstow es un método iterativo, basado en el método de Müller y de
Newton Raphson. Dado un polinonio fn(x)
se encuentran dos factores, un polinomio cuadrático f2(x) = x2 – rx – s y fn-2(x). El procedimiento general para el método de
Bairstow es:
- Dado
fn(x) y r0
y s0
- Utilizando
el método de NR calculamos f2(x)
= x2 – r0x – s0 y fn-2(x), tal que, el
residuo de fn(x)/ f2(x)
sea igual a cero.
- Se
determinan la raíces f2(x),
utilizando la formula general.
- Se
calcula fn-2(x)= fn(x)/ f2(x).
- Hacemos
fn(x)= fn-2(x)
- Si
el grado del polinomio es mayor que tres regresamos al paso 2
- Si
no terminamos
La principal diferencia de este método,
respecto a otros, es que permite calcular todas las raíces de un polinomio
(reales e imaginarias).
Para calcular la división de polinomios,
hacemos uso de la división sintética. Así dado
fn(x) = anxn
+ an-1xn-1 + … + a2x2 + a1x
+ a0
Al dividir entre f2(x) = x2 – rx – s, tenemos como resultado
el siguiente polinomio
fn-2(x) = bnxn-2
+ bn-1xn-3 + … + b3x + b2
con un residuo R = b1(x-r) + b0, el residuo será cero solo si b1 y b0 lo
son.
Los términos b, los calculamos utilizamos división sintética, la cual puede
resolverse utilizando la siguiente relación de recurrencia
bn = an
bn-1 = an-1
+ rbn
bi = ai + rbi+1 + sbi+2
Una manera de determinar los
valores de r y s que hacen cero el residuo es utilizar el Método de
Newton-Raphson. Para ello
necesitamos una aproximación lineal de b1 y b0 respecto a r y s la
cual calculamos utilizando la serie de Taylor
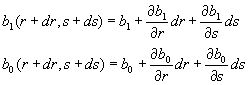
donde los valores de r y s están dados y calculamos los incrementos dr y ds que hacen a b1(r+dr, s+ds) y b0(r+dr, s+dr) igual a cero. El sistema de ecuaciones que tenemos que resolver es:
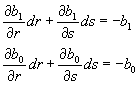
Bairtow muestra que las derivadas parciales pueden obtener haciendo un procedimiento similar a la división sintética, así
cn = bn
cn-1 = bn-1
+ rcn
ci = bi
+ rci+1 + sci+2
donde
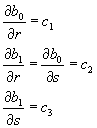
Sustituyendo término
Ejemplo 1
Dado el polinomio f5(x) = x5 - 3.5x4 + 2.75x3 + 2.125x2 - 3.875x + 1.25, determinar los valores de r y s que hacen el resido igual a cero. Considere r0 = -1 y s0 = 2.
Solución.
Iteración 1.
La división sintética con el polinomio f2(x) = x2 -x + 2.0 da como resultado
f3(x) = x3 - 4.5x2 + 9.25x - 16.125 Residuo = {30.75, -61.75}
Aplicando el método de Newton tenemos
|
-43.875 |
16.75 |
|
dr |
|
-30.75 |
|
108.125 |
-43.875 |
|
ds |
|
61.75 |
de donde
r1 = -1.0 + 2.7636812508572213 =1.7636812508572213
s1 = 2.0 + 5.403374022767796 =7.403374022767796
Iteración 2.
La división sintética con el polinomio f2(x) = x2 -1.7636812508572213x - 7.403374022767796 da como resultado
f3(x) = x3 - 1.7363187491427787x2 +
7.091061199392814x - 1.776754563401905
Residuo = {51.75640698828836, 105.68578319650365}
Aplicando el método de Newton tenemos
|
27.628006 |
14.542693 |
|
dr |
|
-51.75640 |
|
208.148405 |
27.62800 |
|
ds |
|
-105.68578 |
de donde
r2 = 1.7636812508572213 - 0.04728019113442016 = 1.7164010597228012
s2 = 7.403374022767796 - 3.469106187802152 = 3.934267834965644
Iteración 3.
La división sintética con el polinomio f2(x)= x2 - 1.7164010597228012x - 3.934267834965644 da como resultado
f3(x) = x3 - 1.7835989402771988x2
+ 3.622896723753395x + 1.3261878347051992
Residuo = {12.654716254544885, 28.1881465309956}
Aplicando el método de Newton tenemos
|
13.83497 |
7.44182 |
|
dr |
|
-12.65471 |
|
65.679212 |
13.83497 |
|
ds |
|
-28.18814 |
de donde
r3 = 1.7164010597228012 - 0.11666951305731528 = 1.599731546665486
s3 = 3.934267834965644 - 1.4835870659929915 = 2.4506807689726524
En resumen
|
k |
r |
s |
Residuo |
|
|
0 |
-1 |
2 |
30.75 |
-61.75 |
|
1 |
1.76368 |
7.403374 |
51.756406 |
105.68578 |
|
2 |
1.71640 |
3.93426 |
12.65471 |
28.18814 |
|
3 |
1.599731 |
2.450680 |
2.89958 |
8.15467 |
|
4 |
1.33354 |
2.18666 |
0.760122 |
2.522228 |
|
5 |
1.11826 |
2.11302 |
0.271940 |
0.607688 |
|
6 |
1.02705 |
2.02317 |
0.04313 |
0.11185 |
|
7 |
1.00165 |
2.00153 |
0.00277 |
0.00634 |
|
8 |
1.00000 |
2.00000 |
1.13930E-5 |
2.67534E-5 |
La solución es:
f3(x) = x3 - 2.53x2
+ 2.25x - 0.625 y f2(x) = x2
- x - 2
Las raíces de f2(x) = x2
- x - 2, son
x1 = 2
x2 = -1
Si repetimos el ejemplo pero ahora considerando
el polinomio f3(x) = x3 - 2.53x2 + 2.25x -
0.625 , podemos calcular el total de las raíces del polinomio original.
Ejemplo 2
Dado el polinomio f5(x) = x5 - 3.5x4 + 2.75x3
+ 2.125x2 - 3.875x + 1.25, determinar las raíces de este
polinomio. Considere r0 = -1 y s0 = -1.
Paso 1.
f5(x)
= x5 - 3.5x4 +
2.75x3 + 2.125x2 - 3.875x + 1.25
f5(x)
=( x3 - 4x2 + 5.25x - 2.5)*( x2 +0.5x - 0.5)
Las raíces de x2 +0.5x - 0.5=0 son
x1 = 0.5
x2 =-1.0
Paso 2.
f3(x) = x3 - 4x2 + 5.25x - 2.5
f3(x) =(x - 2)*(x2 - 2x +1.25)
Las raíces de x2 - 2x +1.25=0 son
x3 = 1.0 + j0.5
x4 =-1.0 - j0.5
Paso 3
f1(x)
=(x - 2)
La raíz de este polinomio es
x5
= 2;
Todas la raíces de f5(x)
son x = [0.5, 1.0, (1.0 + j0.5), (1
- j0.5), 2]
Implementación en Java.
package ejemplos;
/**
* <p>Title: Meétodo de Baritow </p>
* <p>Description: Calcula todas las raices de un polinomio
de grado n</p>
* <p>Copyright:
Copyright (c) 2003</p>
*
<p>Company: UMSNH</p>
*
@author Dr. Felix Calderon Solorio
* @version 1.0
*/
public class ej065 {
public static
void main(String[] args) {
//double
a[] = {-2.5, 5.25, -4, 1};
double a[]
={1.25, -3.875, 2.125, 2.75, -3.5, 1};
int n =
a.length;
double re[]
= new double[n];
double im[]
= new double[n];
Bairstow(a,
-1, -1, re, im);
//Bairstow(a, -1, 2, re, im);
}
static public
void Bairstow(double a[], double r0, double s0, double re[], double im[])
{
int n =
a.length, iter =0;
double b[]
= new double[n], c[] = new double[n];
double ea1
= 1, ea2 = 1, T = 0.00001;
double
r=r0, s=s0,det, ds, dr;
int MaxIter
= 100, i;
for(iter=0;
iter< MaxIter && n>3; iter++)
{
do {
Division_Derivada(a,
b, c, r, s, n);
/*
System.out.println("Solucionando ");
System.out.print("fn(x) = "); imprime(a, n);
System.out.print("fn-2(x) = "); imprime2(b, n);
System.out.println("f2(x) = x2 + " + r + "x + " + s);
System.out.println(c[2] + " " + c[3] + " = " +
-b[1]);
System.out.println(c[1] + " " + c[2] + " = " +
-b[0]);
*/
det =
c[2]*c[2] - c[3]*c[1];
if(det!=0)
{
dr =
(-b[1]*c[2] + b[0]*c[3])/det;
ds =
(-b[0]*c[2] + b[1]*c[1])/det;
/*
System.out.println("*********************************");
System.out.println(r+dr +" = " + r + " + " + dr);
System.out.println(s+ds +" = " + s + " + " + ds);
System.out.println("-----------------------------------");*/
r =
r+dr;
s =
s+ds;
if(r!=0) ea1 = Math.abs(dr/r)*100.0;
if(s!=0) ea2 = Math.abs(ds/s)*100.0;
}
else
{
r =
5*r+1;
s =
s+1;
iter = 0;
}
}
while ((ea1 > T) &&
(ea2 > T));
raices(r, s, re, im, n);
System.out.println("iter " +iter);
System.out.print("fn(x) = "); imprime(a, n);
System.out.print("fn-2(x) = "); imprime2(b, n);
System.out.println("f2(x)
= x2 -(" +r + ")x -(" +s +")");
n = n-2;
for(i=0;
i<n; i++)
a[i] =
b[i+2];
if (n
< 4) break;
}
if(n==3)
{
System.out.println("n = " + n);
r =
-a[1]/a[2];
s =
-a[0]/a[2];
imprime(a, n);
raices(r,
s, re, im, n);
}
else
{
re[n-1] =
-a[0]/a[1];
im[n-1] =
0;
}
for(i=1;
i<re.length; i++)
System.out.println( "X["+i+"]= " + re[i] + " j
" + im[i]);
}
public static
void Division_Derivada(double a[], double b[], double c[], double r, double s,
int n)
{
int i;
b[n-1] =
a[n-1];
b[n-2] =
a[n-2] + r*b[n-1];
c[n-1] =
b[n-1];
c[n-2] =
b[n-2] + r*c[n-1];
for(i=n-3;
i>=0; i--)
{
b[i] =
a[i] + r*b[i+1] + s*b[i+2];
c[i] =
b[i] + r*c[i+1] + s*c[i+2];
}
}
public static
void imprime(double x[], int n)
{
int i;
for (i = n
- 1; i >= 0; i--)
if(x[i]
> 0) System.out.print("+ " +x[i] + "x"+i+" ");
else System.out.print("-
" + -x[i] + "x"+i+" ");
System.out.println("");
}
public static
void imprime2(double x[], int n)
{
int i;
for (i = n
- 1; i >= 2; i--)
if(x[i]
> 0) System.out.print("+ " +x[i] + "x"+(i-2)+"
");
else System.out.print("-
" + -x[i] + "x"+(i-2)+" ");
System.out.println("Residuo = {"+ x[1]+ ", " + x[0]
+ "}");
}
public static
void raices(double r, double s, double re[], double im[], int n)
{
double d =
r*r + 4*s;
if(d >
0)
{
re[n-1] = (r + Math.sqrt(d))/2.0;
re[n-2] =
(r - Math.sqrt(d))/2.0;
im[n-1] =
0;
im[n-2] =
0;
}
else
{
re[n-1] =
r/2.0;
re[n-2] =
re[n-1];
im[n-1] =
Math.sqrt(-d)/2.0;
im[n-2] =
-im[n-1];
}
}
}