Búsqueda con incrementos.
Como se ha mencionado, el graficar a función de la cual se desea calcular su raíz, es de mucha utilidad. Si queremos que esta tarea se realice de manera automática, una forma de hacerlo es por medio de incrementos.
Seleccionar un incremento no es tarea fácil,
así por ejemplo, en la siguiente figura podemos ver, la gráfica de la función f(x)=sen10x
+ cos 3x
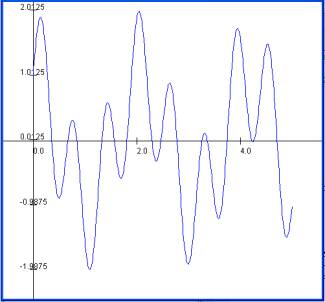
Así por ejemplo si tomamos dos puntos x1=0
y x2 = 2, las funciones valuadas en estos valores son f(0)
=0.841470985 y f(2)= 0.85780222,
podríamos suponer que la función crece en la dirección positiva de x, cuando en
realidad en este intervalo existen 6 raíces.
Ahora si tomamos el intervalo x1=0 y x2
= 1 las funciones valuadas en estos valores son f(0) =0.841470985 y f(2)= 0.402979862, podríamos pensar
que más adelante existe una raíz, cuando en realidad en este intervalo existen
más de una.
Una manera de solucionar este problema es poner
un punto inicial x0 y un incremento h lo
suficientemente pequeño para evitar las situaciones antes descritas. El
algoritmo consiste en:
1.- Dado x0 y h,
hacemos k = 1
2.- Calculamos xk = xk-1 +
h
3.- Duplicamos el incremento h = 2*h
4.- Si f(x0) * f(xk)
< 0 paramos, sino regresamos a 2.
Para nuestra función tenemos:
|
h |
xk |
f(xk) |
|
|
0.000 |
0.841 |
|
0.001 |
0.001 |
0.847 |
|
0.002 |
0.003 |
0.857 |
|
0.004 |
0.007 |
0.877 |
|
0.008 |
0.015 |
0.912 |
|
0.016 |
0.031 |
0.965 |
|
0.032 |
0.063 |
0.999 |
|
0.064 |
0.127 |
0.809 |
|
0.128 |
0.255 |
-0.129 |
|
0.256 |
0.511 |
-0.907 |
|
0.512 |
1.023 |
0.191 |
|
1.024 |
2.047 |
0.507 |
Podemos ver que con un incremento de 0.001, hemos
localizado una raíz en el intervalo x = [0.000, 0.255]. Esta es la información que utilizamos para
inicializar, ya sea, el método de Regula Falsi o Bisecciones.