Interpolación
cuadrática
La interpolación cuadrática tiene la ventaja
del hecho que un polinomio de segundo orden con frecuencia proporciona una
buena aproximación a la forma de f(x)
cercana un óptimo.
Este método al igual que el de Muller hacen una
aproximación cuadrática de un polinomio, así f(x) = Ax2 + Bx + C. Para esta función el mínimo o
máximo se localiza en
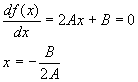
Se puede mostrar que después de un manejo
algebraico el valor de x3
que maximiza la ecuación es:
![]()
Algoritmo
1.- Dados tres puntos x0, x1 y x2
dentro de los cuales existe un máximo y x0
< x1 < x2
2.- Calculamos la aproximación cuadrática y su
máximo x3 utilizando la
ecuación anterior.
3.- Si x0
< x3 < x1, los nuevos puntos de búsqueda son x0, x3 y x1,
si no el intervalo de búsqueda es x1,
x3 y x2
4.- Se repiten los pasos hasta que la
diferencia entre x0 y x2 sea pequeña.
Ejemplo
Use la búsqueda de la sección dorada para
encontrar el máximo de la función f(x) = 2seno(x) – x2/10 con
los valores iniciales x0 = 0,
x1 = 1 y x2 = 4.
|
i |
x0 |
f0 |
x1 |
f1 |
x2 |
f2 |
x3 |
f3 |
|
0 |
0.0000 |
0.0000 |
1.0000 |
1.5829 |
4.0000 |
-3.1136 |
1.5055 |
1.7691 |
|
1 |
1.0000 |
1.5829 |
1.5055 |
1.7691 |
4.0000 |
-3.1136 |
1.4903 |
1.7714 |
|
2 |
1.0000 |
1.5829 |
1.4903 |
1.7714 |
1.5055 |
1.7691 |
1.4256 |
1.7757 |
|
3 |
1.0000 |
1.5829 |
1.4256 |
1.7757 |
1.4903 |
1.7714 |
1.4266 |
1.7757 |
|
4 |
1.4256 |
1.7757 |
1.4266 |
1.7757 |
1.4903 |
1.7714 |
1.4275 |
1.7757 |
|
5 |
1.4266 |
1.7757 |
1.4275 |
1.7757 |
1.4903 |
1.7714 |
1.4276 |
1.7757 |
Implementación en Java
void Interpolacion_Cuadratica()
{
double x0, x1, x2, x3;
double f0, f1, f2,
num, den;
int i = 0;
x0 = 0;
x1 = 1;
x2 = 4;
System.out.println("i" +
"\t" + "x0" + "\t" + "f0" +
"\t" + "x1" + "\t" + "f1" +
"\t" +
"x2" + "\t" + "f2" + "\t" +
"x3" + "\t" + "f3");
do
{
f0 =
funcion(x0);
f1 =
funcion(x1);
f2 = funcion(x2);
den
= f0*(x1*x1 - x2*x2) + f1*(x2*x2 - x0*x0) + f2*(x0*x0 - x1*x1);
num = f0*(x1 - x2) + f1*(x2 - x0) +
f2*(x0 - x1);
x3 = den/(2.0*num);
System.out.println(i++ + "\t"
+ x0 + "\t" + f0 + "\t" + x1 + "\t" + f1 +
"\t"
+ x2 + "\t" + f2 + "\t" + x3 + "\t" + funcion(x3)
);
if(x0
<= x3 && x3 <= x1)
{
x2 = x1;
x1 = x3;
}
else
{
x0 = x1;
x1 = x3;
}
}while(x3-x0 >= 0.0001);
}