Método de la Secante.
Un problema en la implementación del método de Newton-Raphson es el de la evaluación de la derivada. Aunque esto no es un inconveniente para los polinomios y para muchas otras funciones, existen algunas funciones cuyas derivadas pueden ser en extremo difíciles de evaluar. En estos casos, la derivada se puede aproximar mediante una diferencia finita.
![]()
Sustituyendo esta aproximación en la formula de Newton, tenemos la fórmula del método de la secante.
![]()
Ejemplo.
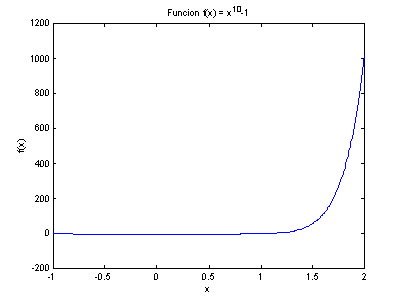
Encontrar la solución utilizando el método de
la secante para la función f(x) = x10 –1.
|
x0 |
x1 |
f(x0) |
f(x1) |
|
0.5000 |
0.9000 |
-0.9990 |
-0.6513 |
|
0.9000 |
1.6493 |
-0.6513 |
147.9235 |
|
1.6493 |
0.9033 |
147.9235 |
-0.6384 |
|
0.9033 |
0.9065 |
-0.6384 |
-0.6253 |
|
0.9065 |
1.0602 |
-0.6253 |
0.7945 |
|
1.0602 |
0.9742 |
0.7945 |
-0.2301 |
|
0.9742 |
0.9935 |
-0.2301 |
-0.0630 |
|
0.9935 |
1.0008 |
-0.0630 |
0.0080 |
|
1.0008 |
1.0000 |
0.0080 |
-0.0002 |
Note, que para este problema, el método de la
secante si lleva a una solución. Este hecho se debe a que calcula su
aproximación apoyada de dos puntos, no de uno solo.
La implementación de este método en Java es :
double Secante()
{
int i;
double m, x, x0 = 0, h = 0.5;
x = inicio + h;
while(Math.abs(f(x))
> 0.0001)
{
m = (f(x) - f(x0))/(x - x0);
x0 = x;
x = x - f(x)/m;
}
return x;
}
Su ejecución puede verse [aquí].