Matrices Especiales.
Una matriz
bandada es una matriz cuadrada en la
que todos sus elementos son cero, con excepción de una banda sobre la diagonal
principal. Un sistema tridiagonal (es decir con un ancho de banda de 3) se
puede expresar en forma general como:
|
f0 |
g0 |
|
|
|
x0 |
|
b0 |
|
e1 |
f1 |
g1 |
|
|
x1 |
= |
b1 |
|
|
e2 |
f2 |
g2 |
|
x2 |
|
b2 |
|
|
|
e3 |
f3 |
|
x3 |
|
b3 |
Basados en
la descomposición LU podemos ver que el algoritmo de Thomas es:
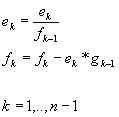
La sustitución hacia adelante es
![]()
y hacia atrás es:
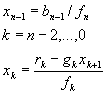
Ejemplo:
Resuelva el siguiente sistema tridiagonal por
medio del algoritmo de Thomas.
|
2.04 |
-1 |
|
|
|
x0 |
|
40.8 |
|
-1 |
2.04 |
-1 |
|
|
x1 |
= |
0.8 |
|
|
-1 |
2.04 |
-1 |
|
x2 |
|
0.8 |
|
|
|
-1 |
2.04 |
|
x3 |
|
200.8 |
La solución de la descomposición triangular es:
|
2.04 |
-1 |
|
|
|
-0.49 |
1.55 |
-1 |
|
|
|
-0.645 |
1.395 |
-1 |
|
|
|
-0.717 |
1.323 |
La solución del sistema es:
X = [65.970, 93.778, 124.538, 159.480]T
Descomposición
de Cholesky.
Este algoritmo se basa en el hecho de que una
matriz simétrica se puede descomponer en [A] = [L][L]T , dado que la
matriz [A] es una matriz simétrica. En este caso aplicaremos la eliminación de
Crout a la parte inferior de la matriz y la parte superior, simplemente tendrá
los mismos valores.
Así tomando las ecuaciones para la factorización
LU la podemos adaptar como:
Podemos ver, que cualquier elemento bajo la
diagonal se calcula como:
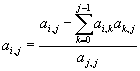
para todo i=0,...,n-1
y j = 0,...,i-1.
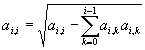
para todo i=0,...,n-1.
La
implementación en Java es:
static public void
Cholesky(double A[][]) {
int i, j, k, n, s;
double fact, suma = 0;
n
= A.length;
for (i = 0; i < n; i++) { //k = i
for (j = 0; j <= i - 1; j++) { //i = j
suma = 0;
for (k = 0; k <= j - 1; k++) // j = k
suma += A[i][k] * A[j][k];
A[i][j] = (A[i][j] - suma) / A[j][j];
}
suma = 0;
for (k = 0; k <= i - 1; k++)
suma += A[i][k] * A[i][k];
A[i][i] = Math.sqrt(A[i][i] - suma);
}
}