Métodos basados en
gradiente
Como su nombre lo indica, son métodos para
calcular el óptimo de una función, basados en la información del
gradiente.
El gradiente.
Dada una función en dos dimensiones f(x,y), las derivada direccional, se
define como
![]()
donde q es la dirección sobre la cual se
quiere calcular la derivada y u es un
vector unitario con la información de la dirección de q. Podemos escribir la derivada
direccional como
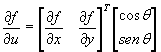
El gradiente se define como el vector de derivadas
en la direcciones de x y y donde el cambio es máximo. La
expresión de este esta dado por
![]()
donde i
y j representan los vectores
unitarios en la direcciones de x y y.
Utilizando la notación vectorial podemos
representar al gradiente como
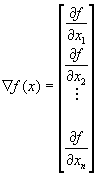
Ejemplo 1
Dada la función f(x,y) = x2 +2x + 3y2, determinar el mínimo
de la función y la dirección hacia donde se encuentra el mínimo en el punto de
coordenadas [2,2].
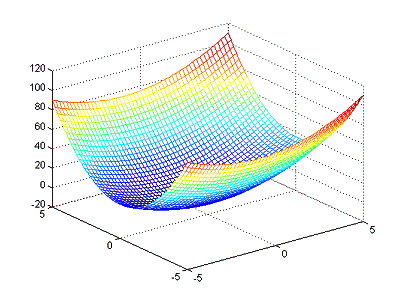
Si calculamos la derivada tenemos e igualamos a
cero
f’x = 2x+2
= 0
f’y = 6y =
0
Note que el mínimo se localiza en el punto
[0,0].
Ahora, si valuamos el gradiente en el punto
[2,2] tenemos que es igual a [6, 12], de manera gráfica tenemos.
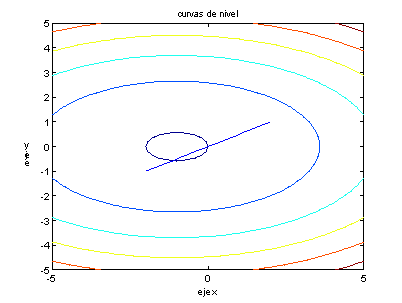
Note como del punto [2,2] puedo acercarme al
mínimo, siguiendo la dirección opuesta al gradiente.![]()
Demostración.
Dada la definición de la derivada direccional,
podemos ver que esta, se puede escribir como el producto escalar de vectores
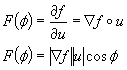
Si queremos determinar la dirección en la cual
la función decrece, calculamos la derivada de F, con respecto a phi.
![]()
Note que el mínimo se encuentra cuando el
ángulo es de 180 grado, lo cual significa que la función decrece en la
dirección opuesta al gradiente y el máximo se encuentra en la dirección del
gradiente.
Método de descenso de
gradiente
Como hemos visto, el máximo de una función se encuentra
en la dirección del gradiente, mientras que un mínimo en la dirección opuesta.
Así podemos plantear una estrategia para alcanzar el mínimo de una función
utilizando un punto inicial, el valor del gradiente y un tamaño de paso a con el cual avanzaremos.
Algoritmo
1.- Dado una posición inicial r(0)
en un espacio n dimensional y una función f(r)
2.- Calculamos el valor del gradiente en ![]()
3.- Hacemos la actualización utilizando la
sucesión ![]()
4.- Si la magnitud del gradiente es cercana a
cero, terminamos, sino hacemos k = k+1
y regresamos a 2.
Implementación en Java
static public void Descenso_Gradiente()
{
double r[] = {2,2};
double u[] = new double[2];
double alfa = 0.01;
int k = 0;
while(gradiente(u, r)
> 0.01)
{
System.out.println(k + " " +
r[0] + " " + r[1] + " " + f(r));
gradiente(u,
r);
r[0] -= alfa*u[0];
r[1] -= alfa*u[1];
k
++;
}
}
public static double f(double r[])
{
return r[0]*r[0] +2.0*r[0] +
3.0*r[1]*r[1];
}
public static double gradiente(double u[],
double r[])
{
double mag;
u[0] = 2.0*r[0] + 2.0;
u[1] = 6.0*r[1];
mag = Math.sqrt(u[0]*u[0] + u[1]*u[1]);
u[0] /= mag;
u[1] /= mag;
return mag;
}
Problema para
seleccionar el tamaño de paso
La solución del ejemplo 1 utilizando un tamaño
de paso de 0.01 es:
|
k |
x |
y |
f(x,y) |
|
0 |
2.0000 |
2.0000 |
20.0000 |
|
1 |
1.9955 |
1.9911 |
19.8661 |
|
2 |
1.9910 |
1.9821 |
19.7327 |
|
3 |
1.9866 |
1.9732 |
19.5998 |
|
4 |
1.9820 |
1.9643 |
19.4675 |
|
5 |
1.9775 |
1.9553 |
19.3357 |
|
6 |
1.9730 |
1.9464 |
19.2044 |
|
7 |
1.9685 |
1.9375 |
19.0736 |
|
8 |
1.9639 |
1.9286 |
18.9433 |
|
9 |
1.9594 |
1.9197 |
18.8135 |
|
|
|
|
|
|
387 |
-0.9879 |
0.0000 |
-0.9999 |
Podríamos suponer que un tamaño de paso mas
grande hará que el algoritmo converja mas rápido, así que para un tamaño de
paso de 0.5 tenemos
|
k |
x |
y |
f(x,y) |
|
0 |
2.0000 |
2.0000 |
20.0000 |
|
1 |
1.7764 |
1.5528 |
13.9418 |
|
2 |
1.5204 |
1.1233 |
9.1378 |
|
3 |
1.2209 |
0.7229 |
5.5003 |
|
4 |
0.8632 |
0.3736 |
2.8902 |
|
5 |
0.4347 |
0.1159 |
1.0987 |
|
6 |
-0.0512 |
-0.0019 |
-0.0998 |
|
7 |
-0.5512 |
0.0011 |
-0.7986 |
|
8 |
-1.0512 |
-0.0025 |
-0.9974 |
|
9 |
-0.5566 |
0.0710 |
-0.7883 |
|
|
|
|
|
|
4680 |
-1.0000 |
-0.1456 |
-0.9364 |
Note que después de 4680 iteraciones no hemos
convergido y que pasa si utilizamos un tamaño de paso de 0.005
|
k |
x |
y |
f(x,y) |
|
0 |
2.0000 |
2.0000 |
20.0000 |
|
1 |
1.9978 |
1.9955 |
19.9330 |
|
2 |
1.9955 |
1.9911 |
19.8661 |
|
3 |
1.9933 |
1.9866 |
19.7993 |
|
4 |
1.9910 |
1.9821 |
19.7327 |
|
5 |
1.9888 |
1.9777 |
19.6662 |
|
6 |
1.9865 |
1.9732 |
19.5998 |
|
7 |
1.9843 |
1.9687 |
19.5336 |
|
8 |
1.9820 |
1.9643 |
19.4675 |
|
9 |
1.9798 |
1.9598 |
19.4015 |
|
|
|
|
|
|
775 |
-0.9936 |
0.0000 |
-1.0000 |
Note que la convergencia es más lenta, pero la
precisión obtenida es mejor. La selección del tamaño del paso es un proceso complicado
donde este valor quedará sujeto a las características del problema y no existe
regla general para seleccionarlo.
Hessiano
Cuando calculamos el gradiente de una función e
igualamos este a cero, estamos calculando un punto que puede ser máximo o
mínimo. Una manera de saber si estamos en un máximo o un mínimo es hacer una
evaluación sobre la segunda derivada. Así estaremos en un mínimo si la segunda
derivada es positiva y en un máximo si la segunda derivada es negativa.
En el caso de funciones de varias variables,
dado que se tiene una función que depende de varias variables, es común
representarla en una matriz de segundas derivadas a las que se les denomina
Hessiano. El Hessiano de una matriz de dos variables se define como:
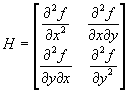
En este caso tendremos un mínimo local si el
determinante de H es positivo o un máximo local si el determinante es negativo.
Ejemplo 2
Determinar para el ejemplo 1, si se trata de un
mínimo o un máximo.
Calculamos la matriz de segundas derivadas y
las evaluamos en cero
![]()
Note que el determinante es positivo, lo cual
indica que en la posición [0,0] se tiene un mínimo.
El método de Newton
El método de Newton esta basado en la
minimización de una función cuadrática. Esta función cuadrática es calculada a
partir de la serie de Taylor
![]()
donde ![]() .
.
Si calculamos el máximo de q(X) tenemos
![]()
Despejando tenemos, que el mínimo de la
aproximación cuadrática lo obtenemos resolviendo el siguiente sistema lineal de
ecuaciones.
![]()
Algoritmo
1. Dado una función y un punto inicial X(0)
2. Determinamos el Gradiente de la función g(X(k))
3. Calculamos el valor del Hessiano de la
función H(X(k))
4. Resolvemos el sistema de ecuaciones H(X(k))dx= g(X(k))
5. Actualizamos el valor de X(k+1) = X(k) – dx
6. Si la magnitud del gradiente es pequeña
terminamos, si no hacemos k = k+1 y
regresamos a 2.
Ejemplo
Dada la función f(x,y) = x2 +2x + 3y2, determinar el mínimo
de la función dado el punto inicial X(0) = [2,2].
El gradiente de la función es
![]()
El Hessiano es
![]()
El sistema de ecuaciones que debemos resolver
es
![]()
La solución del sistema es dx = 3 y dy = 2, con lo cual, los nuevos valores son x=1 y y = 0. Note que solo fue necesaria una iteración, esto se debe a que
la aproximación cuadrática es exacta.
Ejemplo
Dada la función f(x,y) = 100(x2-y)2 +(1-x)2
determinar el mínimo dado como valor inicial X(0) = [10, 10]
El gradiente de la función es
El Hessiano es
|
400(x2 - y)*x - 2(1 - x) |
|
-200 (x2 - y) |
El sistema de ecuaciones que debemos resolver
es
|
1200x2 – 400y + 2.0 |
-400x |
|
-400x |
200 |
Primera iteración
En nuestra primera iteración
resolvemos el sistema de ecuaciones
|
116002.0 |
-4000.0 |
|
dx |
= |
360018.0 |
|
-4000.0 |
200 |
|
dy |
|
-18000.0 |
Las actualizaciones son x = 9.999500027776234 y y = 99.99000055552469
Segunda iteración
Resolvemos el sistema de ecuaciones
|
79994.0007 |
-3999.8000 |
|
dx |
= |
17.9999 |
|
-3999.8000 |
200 |
|
dy |
|
-4.9994E-5 |
Las actualizaciones son x = 1.0004 y y = -79.9820
Tercera iteración
Resolvemos el sistema de ecuaciones
|
33195.8812 |
-400.1799 |
|
dx |
= |
32407.7359 |
|
-400.1799 |
200 |
|
dy |
|
-16196.5806 |
Las actualizaciones son x = 1.0004 y y = 1.0008
En resumen tenemos
|
k |
x |
y |
|
1 |
9.99950 |
99.99000 |
|
2 |
1.00045 |
-79.98200 |
|
3 |
1.00045 |
1.00090 |
|
4 |
1.00000 |
1.00000 |
|
5 |
1.00000 |
1.00000 |
|
6 |
1.00000 |
1.00000 |
|
7 |
1.00000 |
1.00000 |
|
8 |
1.00000 |
1.00000 |
|
9 |
1.00000 |
1.00000 |
|
10 |
1.00000 |
1.00000 |
La implementación en Java de este ejemplo es:
public
class ej033 {
public static void main(String[] args) {
}
public static void
{
int n = 2;
double x[] = {10, 10};
double g[] = new double[n];
double dx[] = new double[n];
double H[][] = new double[n][n];
int i, k;
for(k=1; k<20; k++)
{
gradiente(g, x);
Hessiano(H,
x);
slineal.SolucionLU(H,
dx, g);
System.out.print(k
+ "\t");
for(i=0; i<n; i++)
{
x[i] -= dx[i];
System.out.print(x[i] +
"\t");
}
System.out.println();
}
}
public static void gradiente(double g[],
double x[])
{
g[0] =
400.0*(x[0]*x[0] - x[1])*x[0] - 2.0*(1 - x[0]);
g[1] = -200.0*(x[0]*x[0] - x[1]);
}
public static void Hessiano(double H[][],
double x[])
{
H[0][0] =
1200.0*x[0]*x[0] - 400.0*x[1] + 2.0;
H[0][1] = -400.0*x[0];
H[1][0] = -400.0*x[0];
H[1][1] = 200.0;
}
}