El Método de
Newton-Raphson.
Si tenemos
una función f(x) continua y cerca de
una raíz p. Si la derivada f’(x)
existe, entonces puede utilizarse para desarrollar algoritmos que produzcan
sucesiones {pk} que converjan a p más rápidamente que los algoritmos de
bisección.
Consideremos
el caso de una función como la que se muestra en la figura.
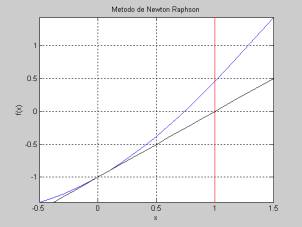
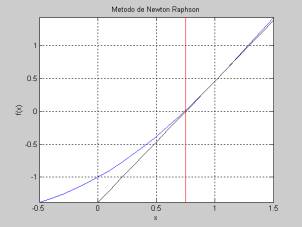
Dos iteraciones del método de
Newton.
En estas
figuras se muestra dos iteraciones del método. En la figura de la izquierda
mostramos la línea recta que es tangente a la función f(x) (en negro), note que la línea recta cruza el eje x en x = 1. A la derecha tenemos la segunda
iteración tomando como valor inicial x=1.
Note como poco a poco se acerca a la solución.
La sucesión
que nos lleva a la solución esta dada por los puntos {p0, p1, p2, …, pk}. La
pendiente de la línea recta es
m = (0 – f(p0))/(p1 – p0)
Por otro lado sabemos, del cálculo diferencial,
que la pendiente de la línea tangente a una función es la primer derivada
valuada en ese punto. Así:
m = f’(p0)
Uniendo las ecuaciones tenemos
f’(p0) = (0 – f(p0))/(p1 – p0)
p1= p0 -
f(p0)/ f’(p0)
De manera iterativa podemos hacer
p2= p1 - f(p1)/ f’(p1)
p3= p2 - f(p2)/ f’(p2)
pk+1= pk - f(pk)/ f’(pk)
Ejemplo.
Hacer un algoritmo iterativo que permita hacer el cálculo de la raíz cuadrada de A.
Para este caso nuestra función a
resolver es f(x) = x2-A. La
solución cuando f(x)=0 es x = A-0.5.
f(x) = x2-A
f’(x) =2 x
pk+1= pk - f(pk)/ f’(pk)
pk+1= pk - (pk-2-A))/(2 pk)
pk+1=( pk + A/ pk)/2
Los cálculos numéricos suponiendo A=5 son:
|
k |
pk |
|
0 |
2.0000 |
|
1 |
2.2500 |
|
2 |
2.2361 |
|
3 |
2.2361 |
|
4 |
2.2361 |
|
5 |
2.2361 |
|
6 |
2.2361 |
|
7 |
2.2361 |
|
8 |
2.2361 |
|
9 |
2.2361 |
|
10 |
2.2361 |
Ejemplo
Calcular los ceros de la función x-cos(x) utilizando el algoritmo de regula falsi en el intervalo [0,1].
|
k |
pk |
|
0 |
0.0000 |
|
1 |
1.0000 |
|
2 |
0.7504 |
|
3 |
0.7391 |
|
4 |
0.7391 |
|
5 |
0.7391 |
|
6 |
0.7391 |
|
7 |
0.7391 |
Método de Newton Raphson para sistemas no lineales
Consideremos el sistema
![]()
Utilizando la serie de Taylor podemos hacer una aproximación lineal
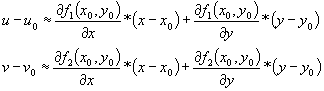
Si escribimos el sistema original como una función vectorial V=F(X), entonces la matriz jacobiana J(x,y) es el análogo bidimensional de la derivada. La aproximación lineal queda como:
![]()
donde
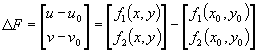
Entonces nuestra formulación bidimensional queda como:
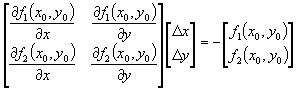
y la actualización de la variable la hacemos:
![]()
Ejemplo.
Resolver el siguiente sistema de ecuaciones dado por
f1(x,y)
= x2 – 2x – y +0.5
f2(x,y)
= x2 + 4y2 – 4
El jacobiano es
![]()
Considerando como valores iniciales [0, 1] tenemos:
Primer iteración
![]()
cuya solución es Dx=
0.25 y Dy =0
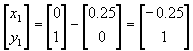
Segunda iteración
![]()
cuya solución es Dx=
-0.0274 y Dy =0.0061
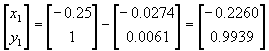
Las demás iteraciones la resumimos es:
|
k |
x |
y |
|
0 |
0.0000 |
1.0000 |
|
1 |
-0.2500 |
1.0000 |
|
2 |
-0.2260 |
0.9939 |
|
3 |
-0.2222 |
0.9938 |
|
4 |
-0.2222 |
0.9938 |
|
5 |
-0.2222 |
0.9938 |
|
6 |
-0.2222 |
0.9938 |
|
7 |
-0.2222 |
0.9938 |
La implementación en
Java de este método es:
double
{
int i;
double m, b, x;
x = 0;
while(Math.abs(f(x)) >
0.0001)
{
m = df(x);
b = - m*x + f(x);
pausa(300);
x = x - f(x)/m;
}
return x;
}
double f(double x)
{
return (x-Math.cos(x));
}
double df(double x)
{
return(1+Math.sin(x));
}
Desventajas del Método de Newton.
Aunque el método de Newton-Raphson en general es muy eficiente, hay situaciones en que se comporta en forma deficiente. Un caso especial, raíces múltiples.
Ejemplo.
Determinar la raíz de la función f(x)
= x10 –1.
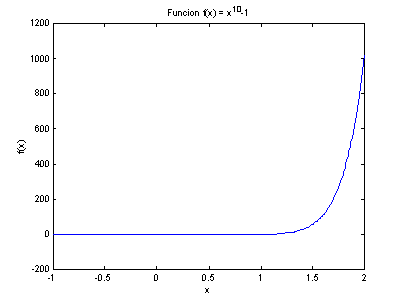
La solución utilizando el método de Newton queda:
![]()
Y la solución numérica es:
|
x |
f(x) |
df(x) |
|
0.5000 |
-0.9990 |
0.0195 |
|
51.6500 |
135114904483914000.0000 |
26159710451871000.0000 |
|
46.4850 |
47111654129711500.0000 |
10134807815362300.0000 |
|
41.8365 |
16426818072478500.0000 |
3926432199748670.0000 |
|
37.6529 |
5727677301318310.0000 |
1521180282851980.0000 |
|
33.8876 |
1997117586819850.0000 |
589336409039672.0000 |
|
30.4988 |
696351844868619.0000 |
228320999775654.0000 |
|
27.4489 |
242802875029547.0000 |
88456233382052.8000 |
|
24.7040 |
84660127717097.5000 |
34269757191973.2000 |
|
22.2336 |
29519161271064.1000 |
13276806089225.7000 |
|
20.0103 |
10292695105054.7000 |
5143706707446.1600 |
|
18.0092 |
3588840873655.1100 |
1992777367871.5700 |
|
16.2083 |
1251351437592.9200 |
772042782329.1500 |
|
14.5875 |
436319267276.5290 |
299105192259.1190 |
|
13.1287 |
152135121499.2910 |
115879479847.7330 |
|
11.8159 |
53046236848.5329 |
44894084747.9692 |
|
10.6343 |
18496079117.2577 |
17392888266.5936 |
|
9.5708 |
6449184014.3077 |
6738361277.7304 |
|
8.6138 |
2248691421.7628 |
2610579221.6818 |
|
7.7524 |
784070216.9426 |
1011391879.0870 |
Su ejecución puede verse [aquí].