Método de Newton
El objetivo de este método es calcular el máximo o mínimo de una función, haciendo uso de una aproximación cuadrática dada por la serie de Taylor. Dicha aproximación cuadrática es:
![]()
![]()
El máximo o mínimo de la función q(x) lo calculamos haciendo q’(x) = 0. Haciendo esto obtenemos
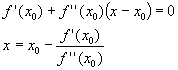
Note que la ecuación resultante es muy similar
a la utilizada en el método de Newton Raphson si la función f(x) es sustituida por f’(x).
Algoritmo
1.- Dado un valor inicial x0 y una función cuyas primera y segunda derivada
existan
2.- Calculamos la i-ésima aproximación
utilizando la formula
![]()
3.- Repetimos el paso dos hasta convergencia.
Ejemplo
Use el método de Newton para encontrar el
máximo de la función f(x) = 2seno(x) – x2/10 con
el valor inicial x0 =2.5.
|
i |
x0 |
x1 |
|
1 |
2.5000 |
0.9951 |
|
2 |
0.9951 |
1.4690 |
|
3 |
1.4690 |
1.4276 |
|
4 |
1.4276 |
1.4276 |
Implementación en Java
void Newton()
{
double x0 = 2.5, x;
int i;
System.out.println("i" +
"\t" + "x0" + "\t" + "x1");
for(i=1; i<1000; i++)
{
x = x0 - Df(x0)/DDf(x0);
System.out.println(i + "\t" +
x0 + "\t" + x);
if(Math.abs(x-x0) <= 0.0001) break;
else x0 = x;
}
}
double Df(double x)
{
return 2.0*Math.cos(x) - 2.0*x/10.0;
}
double DDf(double x)
{
return -2.0*Math.sin(x) - 2.0/10.0;
}