Regresión Lineal

El ejemplo más simple de una aproximación por mínimos cuadrados es mediante el ajuste de un conjunto de pares de observaciones: (x₁, y₁), (x₂, y₂), (x₃, y₃),..., (x_n, y_n ) a una línea recta. La expresión matemática de la línea recta es:

y = a₀ + a₁x + e

donde a₀ y a₁, son los coeficientes que representan el cruce con el eje y y la pendiente de la línea y e representa el error de nuestra aproximación.

Una estrategia, para ajustar a la mejor línea, es minimizar la suma al cuadrado de los errores para todos los datos disponibles

Esta misma ecuación la podemos escribir en forma matricial como

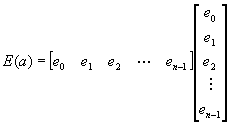
El vector de error en forma matricial queda como

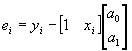
y en general

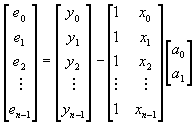
En forma compacta tenemos que e = y – Ma, donde M es la matriz de coordenadas en x y a el vector de parámetros.

Ajuste por mínimos cuadrados

Si queremos encontrar el vector de parámetros a que minimiza nuestra suma de cuadrados, tenemos que calcular la derivada de la función de error respecto al vector de parámetros e igualar a cero.

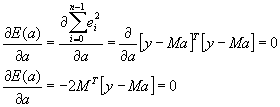
El valor del vector de parámetros a los calculamos resolviendo el siguiente sistema de ecuaciones

[M^TM]a = M^Ty

Es común encontrar la solución de este sistema como:

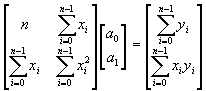
Ejemplo

Hacer el ajuste a una línea recta de los siguientes valores

x	y
1.00	0.50
2.00	2.50
3.00	2.00
4.00	4.00
5.00	3.50
6.00	6.00
7.00	5.50

Aplicando las formulas anteriores, tenemos que el sistema de ecuaciones a resolver es

7	28.00	a0	24.00
28	784.00	a1	119.50

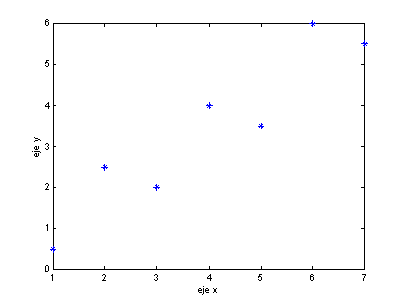
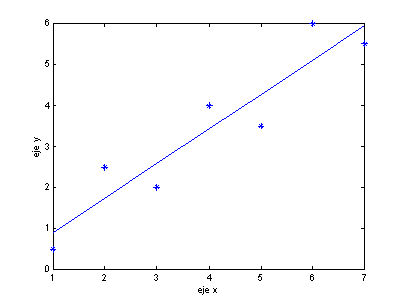
La solución es a = [0.07142, 0.8392] y en la siguiente figura se muestra el ajuste encontrado

Regresión polinomial

Podemos generalizar el caso de la regresión lineal y extenderla a cualquier polinomio de orden m.

[M^TM]a = M^Ty

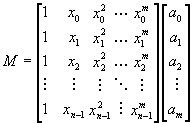
Así por ejemplo la solución para un polinomio de orden 3 es:

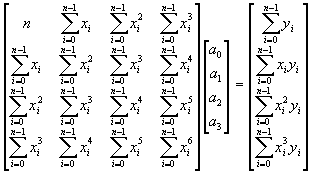
Note que cada uno de los elementos de la matriz M^TM son una sumatoria de todos los valores de x elevado a un exponente que resulta ser la suma del renglón y la columna donde se localiza. Adicionalmente la matriz es simétrica.

El vector de términos independientes es

Ejemplo

Ajustar a un polinomio de segundo orden los datos en la siguiente tabla.

x	y
0.00	2.10
1.00	7.70
2.00	13.60
3.00	27.20
4.00	40.90
5.00	61.10

El sistema de ecuaciones que debemos resolver es:

6.00	15.00	55.00	a[0]		152.60
15.00	55.00	225.00	a[1]	=	585.60
55.00	225.00	979.00	a[2]		2488.80

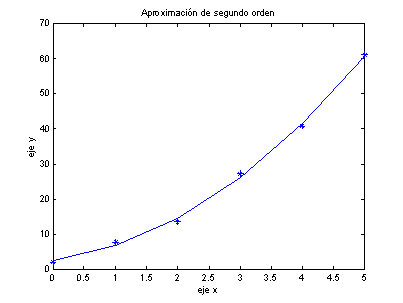
El ajuste da como resultado el polinomio p(x) = 2.4785 + 2.3592x + 1.8607x². En la siguiente figura se muestra la aproximación a un polinomio de segundo orden.

Implementación en Java

public class ej034 {

public static void main(String[] args) {

double x[] = {0, 1, 2, 3, 4, 5};

double y[] = {2.1, 7.7, 13.6, 27.2, 40.9, 61.1};

double a[] = Regresion(x, y, 2);

for(int i=0; i<a.length; i++)

System.out.println("a["+i+"] = "+ a[i]);

grafica(x, y, a);

}

public static double [] Regresion(double x[], double y[], int orden)

{

int i, j, n = orden +1;

double a[] = new double[n];

double MM[][] = new double [n][n];

double My[] = new double[n];

for(i=0; i<n; i++)

{

for (j = 0; j <= i; j++) {

MM[i][j] = sumas(x, i + j);

MM[j][i] = MM[i][j];

}

My[i] = sumas(x, y, i);

}

imprime(MM, My);

slineal.Solucion(MM, a, My);

return a;

}

static public void grafica(double x[], double y[], double a[])

{

int i, j, n = x.length, m = a.length;

double yc[] = new double[n];

for(i=0; i<n; i++)

{

yc[i] =0;

for(j=0; j<m; j++)

yc[i] += a[j] * eleva(x[i], j);

}

grafica g = new grafica("salida");

g.Datos(x, y);

g.Datos(x, yc);

g.show();

}

static public void imprime(double A[][], double b[])

{

int n = b.length;

int i, j;

for(i=0; i<n; i++)

{

for (j = 0; j < n; j++)

System.out.print(A[i][j] + "\t");

System.out.println("\t" + "a["+i+"] \t" + b[i]);

}

}

public static double sumas(double x[], int exp)

{

double suma = 0;

int n = x.length;

for(int k=0; k<n; k++)

suma += eleva(x[k], exp);

return suma;

}

public static double sumas(double x[], double y[], int exp)

{

double suma = 0;

int n = x.length;

for(int k=0; k<n; k++)

suma += eleva(x[k], exp)*y[k];

return suma;

}

public static double eleva(double x, int exp)

{

double resul = 1;

for(int i=1; i<=exp; i++)

resul *= x;

return resul;

}

}

Regresar.