Método de Régula Falsi.

Una de las razones de la introducción de este método es que la velocidad de convergencia del método de bisecciones es bastante baja. En el método de bisección se usa el punto medo del intervalo [a,b] para llevar a cabo el siguiente paso. Suele conseguirse una mejor aproximación usando el punto (c,0) en el que la recta secante L, que pasa por los puntos [a, f(a)] y [b, f(b)].

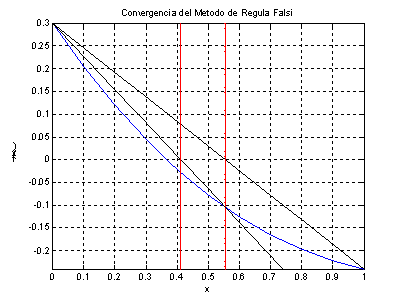
En la figura se puede ver como funciona el método. En esta figura en azul esta la función de la cual queremos calcular el cruce por cero y en negro dos líneas rectas que aproximan la solución.

Para calcula la ecuación de la línea secante hacemos

p₁ = [a, f(a)]

p₂ = [b,f(b)]

y sustituimos en la ecuación de la línea recta.

y – f(a) = (f(b)– f(a))*(x – a)/(b – a)

El cruce por cero de esta ecuación esta en

c = a – f(a)*(b-a)/(f(b) – f(a))

Entonces el método de bisecciones puede ser modificado, en lugar de calcular c = (a+b)/2 hacemos c = a – f(a)*(b-a)/(f(b) – f(a)) y aplicamos las mismas tres reglas de la bisección.

Ejemplo

Calcular los ceros de la función x-cos(x) utilizando el algoritmo de regula falsi en el intervalo [0,1].

iter.	a	c	b	f(a)	f(c )	f(b)
0	0.0000	0.6851	1.0000	-1.0000	-0.0893	-1.0000
1	0.6851	0.7363	1.0000	-0.0893	-0.0047	-0.0893
2	0.7363	0.7389	1.0000	-0.0047	-0.0002	-0.0047
3	0.7389	0.7391	1.0000	-0.0002	0.0000	-0.0002
4	0.7391	0.7391	1.0000	0.0000	0.0000	0.0000
5	0.7391	0.7391	1.0000	0.0000	0.0000	0.0000
6	0.7391	0.7391	1.0000	0.0000	0.0000	0.0000

Ver ejemplo de convergencia.

Regresar.