Búsqueda de la sección dorada
Al resolver para la raíz de sólo una ecuación no lineal, la meta fue la de encontrar la variable x que diera cero en la función f(x). La optimización de una sola variable tiene como meta encontrar el valor de x que generará un extremo, ya sea un máximo o un mínimo de f(x).
La búsqueda de la sección dorada es una técnica simple de búsqueda de una sola variable de propósito general. Es similar en esencia al enfoque de la bisección para localizar raíces
La clave para hacer eficiente este procedimiento es la mejor elección de los puntos intermedios. Esta meta se puede alcanzar al especificar que las siguientes dos condiciones se cumplan.
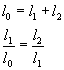
Sustituyendo
la primer ecuación en la segunda tenemos:
![]()
Si tomamos el reciproco y R = l2/l1, se llega a
1 + R = 1/R
R2 + R -
1=0
la cual se puede resolver para la raíz positiva
![]()
Algoritmo
1.- Dados dos puntos iniciales xl y xu, tales que xu > xl y exista un máximo.
2.- Se escogen dos puntos interiores x1 y x2 de acuerdo con la razón dorada,
d = R(xu – xl)
x1 = xl
+ d
x2 = xu
- d
3.- La función se evalúa en los puntos
interiores es decir x1, x2,
xu, y xl
-
Si f(x1) es mayor que f(x2) entonces hacemos xl = x2;
-
Si no xu = x1;
4.- Repetir los pasos 2 y 3 hasta convergencia.
Ejemplo
Use la búsqueda de la sección dorada para
encontrar el máximo de la función f(x) = 2seno(x) – x2/10 en el
intervalo [0,4].
|
i |
xL |
fL |
x2 |
f2 |
x1 |
f1 |
xU |
fU |
d |
|
0 |
0.0000 |
0.0000 |
1.5279 |
1.7647 |
2.4721 |
0.6300 |
4.0000 |
-3.1136 |
2.4721 |
|
1 |
0.0000 |
0.0000 |
0.9443 |
1.5310 |
1.5279 |
1.7647 |
2.4721 |
0.6300 |
1.5279 |
|
2 |
0.9443 |
1.5310 |
1.5279 |
1.7647 |
1.8885 |
1.5432 |
2.4721 |
0.6300 |
0.9443 |
|
3 |
0.9443 |
1.5310 |
1.3050 |
1.7595 |
1.5279 |
1.7647 |
1.8885 |
1.5432 |
0.5836 |
|
4 |
1.3050 |
1.7595 |
1.5279 |
1.7647 |
1.6656 |
1.7136 |
1.8885 |
1.5432 |
0.3607 |
|
5 |
1.3050 |
1.7595 |
1.4427 |
1.7755 |
1.5279 |
1.7647 |
1.6656 |
1.7136 |
0.2229 |
|
6 |
1.3050 |
1.7595 |
1.3901 |
1.7742 |
1.4427 |
1.7755 |
1.5279 |
1.7647 |
0.1378 |
|
7 |
1.3901 |
1.7742 |
1.4427 |
1.7755 |
1.4752 |
1.7732 |
1.5279 |
1.7647 |
0.0851 |
|
8 |
1.3901 |
1.7742 |
1.4226 |
1.7757 |
1.4427 |
1.7755 |
1.4752 |
1.7732 |
0.0526 |
|
9 |
1.3901 |
1.7742 |
1.4102 |
1.7754 |
1.4226 |
1.7757 |
1.4427 |
1.7755 |
0.0325 |
|
10 |
1.4102 |
1.7754 |
1.4226 |
1.7757 |
1.4303 |
1.7757 |
1.4427 |
1.7755 |
0.0201 |
|
11 |
1.4226 |
1.7757 |
1.4303 |
1.7757 |
1.4350 |
1.7757 |
1.4427 |
1.7755 |
0.0124 |
|
12 |
1.4226 |
1.7757 |
1.4274 |
1.7757 |
1.4303 |
1.7757 |
1.4350 |
1.7757 |
0.0077 |
|
13 |
1.4226 |
1.7757 |
1.4256 |
1.7757 |
1.4274 |
1.7757 |
1.4303 |
1.7757 |
0.0047 |
|
14 |
1.4256 |
1.7757 |
1.4274 |
1.7757 |
1.4285 |
1.7757 |
1.4303 |
1.7757 |
0.0029 |
|
15 |
1.4256 |
1.7757 |
1.4267 |
1.7757 |
1.4274 |
1.7757 |
1.4285 |
1.7757 |
0.0018 |
|
16 |
1.4267 |
1.7757 |
1.4274 |
1.7757 |
1.4278 |
1.7757 |
1.4285 |
1.7757 |
0.0011 |
|
17 |
1.4267 |
1.7757 |
1.4271 |
1.7757 |
1.4274 |
1.7757 |
1.4278 |
1.7757 |
0.0007 |
La implementación en Java es:
void Seccion_Dorada()
{
double xL, xU, x1, x2, fL, fU, f1, f2;
double d, R = (Math.sqrt(5)-1.0)/2.0;
int i = 0;
xL = 0;
xU = 4.0;
System.out.println("i" +
"\t" + "xL" + "\t" + "fL" +
"\t" + "x2" + "\t" + "f2" +
"\t" +
"x1" + "\t" + "f1" + "\t" +
"xU" + "\t" + "fU" +
"\t" +
"d");
do
{
d
= R*(xU - xL);
x1 = xL + d;
x2 =
xU - d;
fU = funcion(xU);
fL = funcion(xL);
f1 = funcion(x1);
f2 = funcion(x2);
System.out.println(i++ + "\t"
+ xL + "\t" + fL + "\t" + x2 + "\t" + f2 +
"\t"
+ x1 + "\t" + f1 + "\t" + xU + "\t" + fU +
"\t" + d);
if(f1 > f2) xL = x2;
else xU = x1;
}while(d > 0.001);
}