Factorización triangular.
Supongamos
que la matriz de coeficientes A de un
sistema lineal Ax=b admite una
factorización triangular como la siguiente.
|
a00 |
a01 |
a02 |
|
1 |
0 |
0 |
|
u00 |
u01 |
u02 |
|
a10 |
a11 |
a12 |
= |
l10 |
1 |
0 |
* |
0 |
u11 |
u12 |
|
a20 |
a21 |
a22 |
|
l20 |
l21 |
1 |
|
0 |
0 |
u22 |
Entonces la solución la podemos plantear como
[LU]x = b
El cual se puede solucionar resolviendo primero
Ly=b y luego el sistema Ux=y. Estos sistemas pueden resolverse
utilizando sustitución hacia atrás y sustitución hacia delante.
Sustitución hacia delante.
La
formula para calcular la sustitución hacia delante es:
![]()
La implementación en Java es:
void
sustitucion_hacia_delante(double A[][], double y[], double b[]) {
int k, i, j, n;
double suma;
n = A.length;
for (k = 0; k < n; k++) {
suma = 0;
for (j = 0; j < k; j++) {
suma += A[k][j] * y[j];
}
y[k] =
b[k] - suma;
}
}
Sustitución
hacia atrás.
La
formula para calcular la sustitución hacia atrás es:
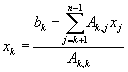
La implementación en Java es:
static
public void sustitucion_hacia_atras(double a[][], double x[], double b[])
{
double suma;
int k, j;
int n = x.length;
for (k = n - 1; k >= 0; k--) {
suma = 0;
for (j = k + 1; j < n; j++)
suma += a[k][j] * x[j];
x[k] =
(b[k] - suma) / a[k][k];
}
}
Ejemplo.
Resolver el sistema de ecuaciones
x0 + 2x1 + 4x2
+ x3 = 21
2x0 + 8x1 + 6x2 + 4x3 = 52
3x0 + 10x1
+ 8x2 + 8x3 = 79
4x0 + 12x1
+ 10x2 + 6x3 = 82
| 1 2 4 1 |
| 1 0 0 0 | | 1
2 4 1 |
A = | 2 8 6 4
| =
| 2 1 0 0 | * | 0 4 –2
2 |
| 3 10 8 8
| | 3 1 1 0 |
| 0 0 –2 3 |
| 4 12 10 6 |
| 4 1 2 1 | | 0
0 0 –6 |
Primero resolvemos el sistema de ecuaciones
y0 = 21
2y0 + y1 = 52
3y0 + y1
+ y2 + = 79
4y0 + y1 + 2y2 + y3
= 82
El cual corresponde a un sistema triangular
inferior
y0 = 21
y1 = 10
y2 = 6
y3 = -24
En general
xk = (bk
– Sj=1,k-1 akj xj)/akk
y posteriormente solucionamos
x0 + 2x1 + 4x2 + x3 = 21
4x1 - 2x2 + 2x3 = 10
- 2x2 + 3x3 = 6
- 6x3 =-24
Utilizando sustitución hacia atrás tenemos
X = [1,2,3,4]T
Implementación utilizando eliminación Gaussiana..
Como vimos una matriz factorizada, fácilmente
puede ser resuelta utilizando los métodos de sustitución hacia adelante y
sustitución hacia atrás. ¿Pero como hacemos la factorización? Comenzaremos por
escribir el sistema
|
a00 |
a01 |
a02 |
|
1 |
0 |
0 |
|
u00 |
u01 |
u02 |
|
a10 |
a11 |
a12 |
= |
l10 |
1 |
0 |
* |
0 |
u11 |
u12 |
|
a20 |
a21 |
a22 |
|
l20 |
l21 |
1 |
|
0 |
0 |
u22 |
A = LU
Si multiplicamos el
primer renglón de L por la primera columna de U tenemos
u00 = a00
u01 = a01
u02 = a02
Ahora hacemos lo
mismo para el segundo renglón de L
|
l10 u00
= a10 |
l10 = a10/u00 |
|
l10 u01
+ u11 = a11 |
u11 = a11
– l10 u01 |
|
l10 u02
+ u12 = a12 |
u12 = a12
– l10 u02 |
Multiplicando el
tercer renglón de L
|
l20 u00
= a20 |
l20 = a20/u00 |
|
l20 u01
+ l21 u11 = a21 |
l21 = (a21
– l20 u01)/a11 |
|
l20 u02
+ l21 u12 + u22 = a22 |
u22 = a22
– l20 u02 – l21 u12 |
Podemos notar lo siguiente, en este caso la triangulación la podemos
hacer en dos pasos.
Paso I. Dado la matriz A hacemos
|
a00 |
a01 |
a02 |
|
a10/a00 |
a11 – a10 a10/a00 |
a12 – a10 a02/a00 |
|
a20/a00 |
a21 – a20 a01/a00 |
a22 – a20 a02/a00 |
|
a00 |
a01 |
a02 |
|
a’10 |
a’11 |
a’12 |
|
a’20 |
a’21 |
a’22 |
Paso II. Dado A
modificada
|
a00 |
a01 |
a02 |
|
a’10 |
a’11 |
a’12 |
|
a’20 |
a’21/ a’11 |
a’22 – a’21a’12/a’11
|
|
a00 |
a01 |
a02 |
|
a’10 |
a’11 |
a’12 |
|
a’20 |
a’’21 |
a’’22 |
Note que para calcular la matriz triangular
superior se podría aplicar, el método de eliminación Gaussiana y la matriz
diagonal inferior es simplemente los cocientes
ajk = ajk/akk
La
implementación en Java es:
static public void LU_EG(double a[][])
{
int n =
a.length;
double
factor;
for (int
k = 0; k <= n - 2; k++) {
for
(int i = k+1; i < n; i++) {
factor = a[i][k]/a[k][k];
a[i][k] = factor;
for
(int j = k+1; j < n; j++)
a[i][j]
-= factor * a[k][j];
}
}
}
Factorización de Crout.
Consideremos un sistema más grande, por ejemplo de 4
ecuaciones con cuatro incógnitas.
|
a00 |
a01 |
a02 |
a03 |
|
1 |
0 |
0 |
0 |
|
u00 |
u01 |
u02 |
u03 |
|
a10 |
a11 |
a12 |
a13 |
= |
l10 |
1 |
0 |
0 |
* |
0 |
u11 |
u12 |
u13 |
|
a20 |
a21 |
a22 |
a23 |
|
l20 |
l21 |
1 |
1 |
|
0 |
0 |
u22 |
u23 |
|
a30 |
a31 |
a32 |
a33 |
|
l30 |
l31 |
l32 |
1 |
|
0 |
0 |
0 |
u33 |
Si hacemos las
multiplicaciones indicadas y dejamos los valores en la misma matriz tenemos:
Para el primer
renglón de la matriz (i=0)
|
|
arriba de la diagonal |
|
j=0 |
a(0,0)
= a(0,0) |
|
j=1 |
a(0,1)
= a(0,1) |
|
j=2 |
a(0,2)
= a(0,2) |
|
j=3 |
a(0,3)
= a(0,3) |
Para el segundo renglón (i=1)
|
|
bajo la diagonal |
|
j=0 |
a(1,0)
= a(1,0) / a(0,0) |
|
|
arriba de la diagonal |
|
j=1 |
a(1,1)
= a(1,1) - a(1,0)a(0,1) |
|
j=2 |
a(1,2)
= a(1,2) - a(1,0)a(0,2)
|
|
j=3 |
a(1,3)
= a(1,3) - a(1,0)a(0,3) |
Tercer renglón (i=2)
|
|
bajo la diagonal |
|
j=0 |
a(2,0)
= a(2,0) /a(0,0) |
|
j=1 |
a(2,1)
= (a(2,1) - a(2,0)a(0,1) )/a(1,1) |
|
|
arriba de la diagonal |
|
j=2 |
a(2,2)
= a(2,2) – a(2,0)
a(0,2) - a(2,1)a(1,2) |
|
j=3 |
a(2,3)=
a(2,3) - a(2,0)a(0,3) - a(2,1)a(1,3) |
Y finalmente para el cuarto renglón (i=3)
|
|
bajo la diagonal |
|
j=0 |
a(3,0)
= a(3,0) / a(0,0) |
|
j=1 |
a(3,1)
= ( a(3,1) - a(3,0) a(0,1) )/a(1,1) |
|
j=2 |
a(3,2)
= (a(3,2)-a(3,0) a(0,2)-a(3,1)
a(1,2) ) / a(2,2) |
|
|
arriba de la diagonal |
|
j=3 |
a(3,3)
= a(3,3) - a(3,0)
a(0,3) - a(3,1) a(1,3) - a(3,2)a(2,3) |
Podemos
ver, que cualquier elemento bajo la diagonal se calcula como:
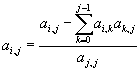
para todo i=0,...,n-1
y j = 0,...,i-1.
![]()
para todo i=0,...,n-1 y j = i,...,n-1.
La implementación en Java es:
static
public void LU(double a[][])
{
int n = a.length;
int i, j, k;
double suma;
for (i = 0; i<n; i++) {
for (j = 0; j <= i-1; j++) {
suma = 0;
for (k = 0; k <= j-1; k++)
suma += a[i][k] * a[k][j];
a[i][j] = (a[i][j] - suma)/ a[j][j];
}
for (j = i; j < n; j++) {
suma = 0;
for (k = 0; k <= i-1; k++)
suma += a[i][k] * a[k][j];
a[i][j] = a[i][j] - suma;
}
}
}
Ejemplo:
Hacer la factorización
LU de la siguiente matriz, utilizando eliminación Gaussiana. Corroborar
utilizando Factorización de Crout.
|
1 |
2 |
4 |
1 |
|
2 |
8 |
6 |
4 |
|
3 |
10 |
8 |
8 |
|
4 |
12 |
10 |
6 |
Paso 1.
|
1 |
2 |
4 |
1 |
|
2 |
4 |
-2 |
2 |
|
3 |
4 |
-4 |
5 |
|
4 |
4 |
-6 |
2 |
Paso 2.
|
1 |
2 |
4 |
1 |
|
2 |
4 |
-2 |
2 |
|
3 |
1 |
-2 |
3 |
|
4 |
1 |
-4 |
0 |
Paso 3.
|
1 |
2 |
4 |
1 |
|
2 |
4 |
-2 |
2 |
|
3 |
1 |
-2 |
3 |
|
4 |
1 |
-2 |
6 |