| Capítulo 2. Codificación de la información | ||
|---|---|---|
 |

|
|
Tabla de contenidos
En este capítulo se estudian las técnicas de codificación de la información utilizadas por un procesador para poder manipular elementos tales como números naturales, enteros, reales, instrucciones, operandos, etc. Todo circuito digital trabaja con lógica binaria, mediante la combinación de múltiples instancias de estos valores se puede construir un esquema de codificación que permite manipular los datos básicos para realizar cálculos.
Los circuitos electrónicos digitales se caracterizan por manipular todas sus señales en dos estados posibles: cero y uno. La información que procesan estos circuitos, por tanto, debe ser representada por tantas unidades de información como sean necesarias, pero siempre y cuando tengan uno de los dos estados posibles. Estas unidades binarias de información se llaman “bits”. Los circuitos digitales, por tanto, están diseñados para operar internamente con bits. Un procesador es un circuito digital capaz de ejecutar un conjunto previamente definido de instrucciones sencillas que se denomina su “lenguaje máquina”.
Pero para la ejecución de este lenguaje máquina es preciso codificar todos los elementos utilizados (números, símbolos, operandos, etc) mediante lógica binaria. Esta codificación es la base para entender cómo un ordenador en cuyo interior sólo existen circuitos capaces de procesar bits puede realizar tareas mucho más sofisticadas.
Un esquema de codificación con bits se define mediante una relación entre los elementos a codificar y un conjunto de cadenas de bits. Cada elemento debe tener al menos una representación en binario, y cada posible cadena de bits, debe corresponder a un elemento. Esta correspondencia debe cumplir una serie de propiedades mínimas para que sea utilizable por los circuitos digitales. Lo más importante es saber de antemano el número de elementos a codificar. Los circuitos digitales sólo pueden manipular códigos binarios de una cierta longitud máxima, y por tanto se debe fijar de antemano. Por ejemplo, si el circuito debe manipular números naturales, se debe escoger de antemano qué subconjunto de estos números se van a utilizar, y de ahí se deduce el número de bits necesarios para su codificación.
Si se utiliza un único bit, se pueden representar únicamente dos elementos, uno con cada uno de los valores posibles, 0 y 1. Si se utilizan cadenas de dos bits, el número de combinaciones posibles aumenta a cuatro: 00, 01, 10, 11. Si el número de bits se incrementa en una unidad, se puede comprobar que el número de combinaciones se duplica pues se pueden obtener dos grupos de combinaciones, uno de ellos con el bit adicional a uno y el otro a cero.
Si con un solo bit se pueden codificar dos elementos, y por cada bit que se añade se duplica el número de combinaciones posible, se deduce por tanto que con n bits se pueden codificar un máximo de 2n elementos.
La fórmula anterior calcula el número de combinaciones posibles al utilizar n bits, pero si se dispone de un conjunto de N elementos, ¿cuántos bits se necesitan para poder codificarlos en binario? Por ejemplo, se dispone de cinco elementos, ¿es posible codificarlos en binario con dos bits? ¿y con tres? ¿y con cuatro? Se precisa un número de bits tal que el número de combinaciones posibles sea mayor al número de elementos. En otras palabras, se precisan n bits siempre y cuando n satisfaga la ecuación 2.1.
Dado un conjunto de N elementos, el número mínimo de bits se obtiene mediante la ecuación 2.2.
donde los símbolos ⌈⌉ representan el entero mayor que el logaritmo obtenido. Por ejemplo, para codificar un conjunto con cinco elementos se debe cumplir n ≥ log25, y por tanto n ≥ 2.3219281, es decir, n ≥ 3.
Esta desigualdad establece un mínimo en el número de bits, pero no un máximo. Efectivamente, si en el ejemplo anterior en lugar de utilizar 3 bits se utilizan más, la codificación es igualmente posible. Para codificar los elementos hay que tener un mínimo de combinaciones binarias, pero se pueden tener combinaciones extras.
Las dos ecuaciones anteriores se pueden transformar en las dos reglas a tener en cuenta en la codificación binaria de elementos:
Con n bits se pueden codificar hasta un máximo de 2n elementos diferentes.
Para codificar N elementos se precisan como mínimo ⌈log2N⌉ bits.
Antes de estudiar cómo se codifican los diferentes elementos con los que trabaja un procesador en binario es útil estudiar la representación de números naturales en diferentes bases. Los números naturales se escriben comúnmente utilizando 10 dígitos, o lo que es lo mismo, en base 10. Dado un número el dígito de menos peso es aquel que corresponde a las unidades, o en general, el que se escribe más a la derecha. Análogamente, el dígito de más peso es el que se escribe más a la izquierda. Un número representado en base b cumple las siguientes condiciones:
Se utilizan b dígitos para representar el número, desde el 0 hasta el b-1.
Al número representado por (b - 1) le sigue el número 10.
Análogamente, al número máximo posible representado por n dígitos le sigue uno con n + 1 dígitos en el que el de más peso es el 1 y el resto son todo ceros.
Las condiciones anteriores se cumplen para los números representados en base 10 donde los dígitos utilizados son del 0 al 9. Al número representado por el dígito de más valor (el 9) le sigue un número de dos dígitos con el segundo dígito de más valor seguido del cero (el 10), y al número máximo posible representado por cuatro dígitos (el 9999) le sigue uno con cinco dígitos que comienza por 1 seguido de cuatro ceros (el 10000).
El valor de un número se obtiene sumando cada uno de los dígitos multiplicado por un factor que representa su peso. Así, de derecha a izquierda, el primer dígito se llama unidades, el segundo decenas, el tercero centenas, y así sucesivamente. En base 10, el valor del número se obtiene multiplicando el dígito de las unidades por uno, el de las decenas por 10, el de las centenas por 100, y así sucesivamente. Tal y como muestra el ejemplo 2.1 para el número 3214.
Los factores por los que se multiplican cada uno de los dígitos son las sucesivas potencias de la base utilizada, en este caso 10. El mismo número se puede reescribir de la siguiente forma:
3214 = 3 * 103 + 2 * 102 + 1 * 101 + 4 * 100.
Es decir, el número se obtiene multiplicando cada dígito por la base elevada a un exponente igual a la posición que ocupa comenzando por el de menos peso cuya posición es cero. La fórmula para obtener el valor del número 3214 se puede reescribir en general como:
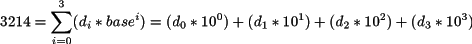
donde di representa el dígito que ocupa la posición i en el número. La fórmula es generalizable para cualquier base. El valor en base 10 de un número de n dígitos escrito en base b se obtiene mediante la ecuación 2.3.
Por ejemplo, el equivalente en base 10 del número 6342 escrito en base 7 se puede obtener mediante la ecuación 2.3:
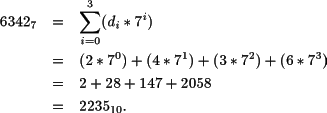
Por tanto, el número 6342 en base 7, corresponde con el número 2235 representado en base 10. El número en base 7 no posee ningún dígito mayor que 6, pues dicha base utiliza sólo los dígitos del 0 al 6.
Al escribir números en diferentes bases aparece un problema de ambigüedad. El número 2235 del ejemplo anterior es el equivalente en base 10 del número 6342 escrito en base 7. Pero a su vez, 2235 es un número válido en base 7 (que es un número válido en base 7 pues sus dígitos son todos menores que 7), aunque tiene otro valor equivalente en base 10. Para evitar la confusión, tal y como muestra la ecuación anterior, cuando se manipulan números en diferentes bases se incluye la base en la que está escrito a la derecha y como un subíndice.
La ecuación 2.3 permite obtener la representación en base 10 de un número en cualquier base. El proceso inverso, es decir, de un número en base 10 obtener su equivalente en una base diferente, es preciso realizar una serie de divisiones sucesivas para obtener los nuevos dígitos comenzando por el de menos peso. El proceso se ilustra con un ejemplo.
Supongamos que se quiere calcular el equivalente en base 7 del número 867510. El dígito de menos peso de la nueva representación se obtiene manipulando la ecuación 2.3:
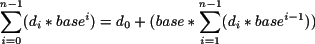
Si se divide la expresión anterior por la base se obtiene como resto el dígito de menos peso d0. El cociente contiene el resto de dígitos y al aplicar sucesivas divisiones se obtiene como resto los dígitos del número en orden creciente de significación.
Por ejemplo, considérese el número 867510. Para obtener su representación en base 7 se realiza la primera división cuyo resto es 2, y por tanto su dígito de menos peso. El cociente resultante es 1239 que se vuelve a dividir por 7 y se obtiene un resto de 0 y un nuevo cociente de 177. Si se repite esta operación sucesivamente, el cociente obtenido será eventualmente 0, y los sucesivos restos corresponden con la representación del número en base 7 tal y como muestra la ecuación 2.4
La aplicación sucesiva de divisiones por la base garantiza que el cociente alcanza siempre un valor menor al de la base. En cuanto se da este caso no es preciso realizar ninguna división más. Se han obtenido los dígitos en base 7 pero la representación sigue siendo consistente con la ecuación 2.3 si se reorganizan los términos tal y como se muestra en la ecuación 2.4:
que corresponde con la codificación en base 7 del número 8675, es decir, 867510=342027.
Como resumen, dado un número en base 10, su representación en base b se obtiene dígito a dígito comenzando por el de menos peso como resto de sucesivas divisiones por la base. El proceso se detiene cuando el cociente final es menor que la base.
Se han descrito los dos procedimientos para traducir un número representado en cualquier base a base 10, y viceversa. Combinando ambos procedimientos se pueden traducir números representados en cualquier base.
El conjunto de datos más simple de codificar en binario para que lo manipule un procesador es el de los números naturales. La representación corresponde con los números en base 2. Los dos únicos dígitos de esta base coinciden con los dos valores que pueden manipular los circuitos digitales.
Dado un número binario con n dígitos, su equivalente en decimal se obtiene aplicando la ecuación 2.3:
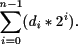
Pero como los dígitos que pueden aparecer en un número binario son 0 o 1, la fórmula anterior se puede interpretar de una forma simplificada. Dado un número representado en base 2, su equivalente en decimal se obtiene sumando aquellas potencias de 2 cuyo exponente corresponde al lugar en el que se encuentra el dígito 1.
Considérese el número en binario 1101011. Su equivalente en decimal se obtiene mediante la siguiente suma:
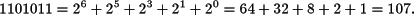
Por tanto, para manipular números codificados en base 2 y saber su equivalente en decimal es importante familiarizarse con los valores de las potencias de 2 que se muestran el la tabla 2.1
Tabla 2.1. Potencias de 2
| Bit | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Peso | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 210 | 211 | 212 | 213 | 214 | 215 |
| Decimal | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 | 32768 |
La tabla 2.2 muestra ejemplos de cómo obtener la representación en decimal de números en binario de ocho bits.
Tabla 2.2. Conversión de binario a decimal
| Peso | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | Total |
|---|---|---|---|---|---|---|---|---|---|
| Binario | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | |
| Decimal | 32 | 4 | 2 | 1 | 39 | ||||
| Binario | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | |
| Decimal | 128 | 32 | 16 | 2 | 178 | ||||
| Binario | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | |
| Decimal | 128 | 64 | 16 | 8 | 1 | 217 | |||
La conversión de un número en base 10 a binario se realiza siguiendo el procedimiento descrito en sección 2.2.1. En este caso, el divisor es 2 y el resto sólo puede ser 0 o 1 produciendo los dígitos de la representación en base 2. Por ejemplo, la representación binaria de 217 se obtiene tal y como muestra la ecuación 2.5
Los dígitos del número en base 2 se obtienen de menor a mayor peso, por tanto el resultado es 11011001 que corresponde con el contenido de la tabla 2.2.
La representación en base 2 tiene ciertas propiedades muy útiles para operar con estos números. Para saber si un número es par o impar basta con mirar el bit de menos peso. Si dicho bit es uno, el número es impar, si es cero, el número es par. La demostración de esta propiedad es trivial. El equivalente en decimal de un número en binario se obtiene sumando potencias de 2. Todas estas potencias, a excepción de la primera (20) son pares. Por tanto, un número impar debe tener un uno en su bit de menos peso. De igual forma, todo número par debe tener un cero en su bit de menos peso, pues sólo puede constar de potencias de 2 pares.
La segunda propiedad no sólo aplica a la base 2, sino a cualquier base. Las operaciones de multiplicación y división entera por la base se realizan añadiendo un cero como dígito de menos peso o quitando el dígito de menos peso respectivamente.
Para los números en base 10, la operación de multiplicación por 10 se realiza añadiendo un cero como dígito de menos peso al número dado. Por ejemplo: 1345 * 10 = 12450. De igual forma, si un número decimal lo dividimos por cero, el cociente se obtiene ignorando el dígito de menos peso, que a su vez corresponde con el resto de la división. Siguiendo con el mismo ejemplo, 1345 dividido entre 10 produce un cociente de 134 y un resto de 5.
Volviendo a la representación binaria, en este caso, la multiplicación y división entera por 2 corresponden de forma análoga con las operaciones de añadir un cero como dígito de menos peso o quitar el dígito de más peso. Por ejemplo, el número binario 100111 que en decimal representa el 39, si se multiplica por 2 se obtiene 1001110 que se puede comprobar que representa el 78 en decimal. Análogamente, si el mismo número se divide entre 2, su cociente es 10011 que representa el número 19, y el resto es 1 (39 = 19 * 2 + 1).
La codificación en base 8 (también denominada codificación octal) a pesar de que aparentemente no es útil en el contexto de la lógica digital, cumple una propiedad especial que la hace importante. Aplicando los conceptos presentados en la sección 2.2 los números codificados en esta base constan de dígitos entre el 0 y el 7. Consecuentemente, tras el 7, el siguiente número es el 10, y tras el 77 el siguiente número es el 100.
Para traducir un número dado en base 10 a base 8 se procede mediante sucesivas operaciones de división entre 8 de las que se obtienen los dígitos correspondientes. En principio es posible realizar una traducción de un número en binario a un número en base 8. Al menos se puede obtener la representación en base 10 del número binario, y luego efectuar su traducción a base 8. Pero, ¿se puede realizar esta traducción directamente?
Analizando las operaciones necesarias para la traducción se descubre esta se puede hacer de forma inmediata. La división entre 8 en números binarios corresponde a una división entre una potencia de la base, más concretamente 23. Tal y como se ha descrito en la sección 2.3, esta operación es equivalente a tres divisiones entre 2, o lo que es lo mismo, a eliminar los tres bits de menos peso del número que a su vez representan el resto de la división. Estos dos resultados son precisamente los que se necesitan para efectuar la traducción.
Por tanto, para traducir un número directamente de binario a base 8 no hay más que agrupar los bits de tres en tres comenzando por los de menor peso, y traducir cada grupo de 3 bits a un dígito entre 0 y 7. Con 3 dígitos binarios se pueden representar exactamente los números del 0 al 7 tal y como muestra la tabla 2.3.
Tabla 2.3. Correspondencia entre grupos de 3 bits y dígitos en octal
| Dígito octal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Binario | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
En el caso de que el último grupo no tenga 3 bits, los bits que faltan se consideran con valor cero (pues los ceros a la izquierda no alteran el valor de un número). La tabla 2.4 muestra un ejemplo de cómo se realiza esta traducción.
Tabla 2.4. Traducción de binario a octal
| Número en Binario | Grupos de 3 bits | Número en Octal | ||
|---|---|---|---|---|
| 001001112 | 000 = 0 | 100 = 4 | 111 = 7 | 478 |
| 101100102 | 010 = 2 | 110 = 6 | 010 = 2 | 2628 |
| 110110012 | 011 = 3 | 011 = 3 | 001 = 1 | 3318 |
Dado lo fácil que es traducir un número de binario a octal y viceversa, esta última base se utiliza como una representación más compacta de los números binarios. En lugar de escribir un conjunto de unos y ceros, se escribe su equivalente en octal. Tan común es esta representación que para denotar que un número está escrito en base 8, en lugar de añadir el subíndice tras el dígito de menos peso, se añade un cero a la izquierda. Por tanto, los números 478 y 047 representan ambos el número 47 en octal.
Este proceso de traducción tan inmediato se deriva de la propiedad de que la base 8 es una potencia de la base 2. Gracias a esta propiedad, las divisiones sucesivas y obtención del resto no es más que agrupar los bits comenzando por el de menos peso.
La base 8 no es la única que tiene esta propiedad. La siguiente base en orden creciente que es también potencia de dos es la base 16. ¿Es posible escribir números en esta base? Siguiendo los conceptos presentados en la sección 2.2 se necesitan tantos dígitos como indica la base comenzando desde el cero. Además de utilizar los diez dígitos del 0 al 9 todavía hacen falta seis dígitos más. La solución es utilizar las seis primeras letras del abecedario: A, B, C, D, E y F. Los 16 dígitos utilizados para representar números en base 16 son:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Aplicando las reglas descritas anteriormente, por ejemplo, al número F le sigue el 10, al 19 le sigue el 1A, al 1F le sigue el 20, al 99 le sigue el 9A, y al 100 le precede el FF.
A esta codificación se le conoce también con el nombre de codificación hexadecimal. ¿Es posible hacer una traducción directa de un número en binario a un número en hexadecimal? La operación necesaria para obtener los dígitos es la división entre 16. Pero, al ser una potencia de 2 (24) la operación consiste en descartar los cuatro bits de menos peso del número binario, que a su vez corresponden con el resto de la división. Por tanto, para obtener un número hexadecimal a partir de un número binario se han de agrupar los bits de cuatro en cuatro comenzando por los de menos peso. Cada uno de ellos se traduce en un dígito hexadecimal. Con 4 bits se codifican exactamente los 16 dígitos que utiliza la base 16 tal y como muestra la tabla 2.5.
Tabla 2.5. Correspondencia entre grupos de 4 bits y dígitos en hexadecimal
| Dígito Hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Binario | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| Dígito Hexadecimal | 8 | 9 | A | B | C | D | E | F |
| Binario | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Al igual que con la base 8, la base hexadecimal se utiliza como representación más compacta de los números en binario. Para evitar la ambigüedad en la representación, un número en hexadecimal se representa añadiendo el prefijo “0x” al comienzo del número. La tabla 2.6 muestra ejemplos de correspondencia entre la representación binaria y la hexadecimal.
Tabla 2.6. Traducción de binario a hexadecimal
| Número en Binario | Grupos de 4 bits | Número en Hexadecimal | |
|---|---|---|---|
| 001001112 | 0010 = 2 | 0111 = 7 | 0x27 |
| 101100102 | 1011 = 11 | 0010 = 2 | 0xB2 |
| 110110012 | 1101 = 13 | 1001 = 9 | 0xD9 |
La conversión de hexadecimal a base 10 se hace de forma idéntica al resto de las bases. Los dígitos de la A a la F tienen valor numérico del 10 al 15, y la base a utilizar es 16. Por ejemplo:
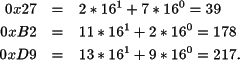
En las secciones anteriores se ha visto cómo codificar números naturales en binario. La representación de un número corresponde con un conjunto de bits. Pero ¿cuántos bits son necesarios para representar los números naturales? Dado que hay infinitos números, la respuesta es infinitos bits. Pero para que un circuito digital sea capaz de manipular este tipo de números, su representación debe tener un tamaño finito.
Esta limitación se traduce en que, además de definir un esquema por el que se codifican los elementos necesarios utilizando el código binario, también se debe fijar el tamaño de dicha codificación y lo que sucede cuando esta codificación no es suficiente. Por ejemplo, se decide representar los números naturales en binario con un tamaño de 10 bits. Sólo los números en el intervalo [0,210 - 1] pueden ser representados. El último número de dicho intervalo es el 1111111111 binario que corresponde con el número 1023 en decimal.
El problema aparece si el procesador manipula los números naturales con 10 dígitos y se debe ejecutar la operación 1023 + 1. El resultado es calculable, pero su representación con 10 bits no es posible. A esta situación, se obtiene un número cuya representación no es posible, se le denomina overflow o “desbordamiento”. Los procesadores detectan y notifican esta situación por tratarse de una anomalía en la codificación.
El número de bits utilizado para codificar los naturales es un parámetro que depende del procesador utilizado. Cuantos más dígitos se utilicen más números se pueden representar, pero a la vez más complicado es el diseño de la lógica interna encargada de realizar las operaciones. A lo largo de la historia, los procesadores han ido utilizando cada vez más bits para representar los números naturales, comenzando por 8 bits (que permiten codificar los números del 0 al 255) hasta los 128 bits de procesadores más avanzados.
El problema del tamaño de la codificación no es único para la representación de números naturales. Cualquier conjunto con un número infinito de elementos a representar en binario tiene el mismo problema. Dependiendo del tamaño de la codificación, tan sólo un subconjunto de sus elementos será representado y el procesador debe detectar y notificar cuando se requiere codificar un elemento cuya representación no es posible.
La codificación de números enteros en binario se puede realizar de diferentes formas. La más sencilla se conoce con el nombre de “signo y magnitud”. Esta codificación está basada en la observación de que todo número entero se puede considerar como un número natural, su valor absoluto, y un signo positivo o negativo. Por ejemplo, el número -345 se puede representar como el par (-, 345). El valor absoluto de un entero, por definición es un número natural, y por tanto se puede utilizar la codificación binaria descrita en la sección 2.3. Respecto al signo, dado que tiene dos posibles valores, su codificación en binario es trivial, con un único bit en el que el valor 0 representa el signo positivo y el valor 1 el signo negativo.
La traducción de un entero en base 10 a su representación en binario en signo y magnitud es directa: se codifica el valor absoluto como un número natural y el signo utilizando un bit adicional. El bit de signo se escribe como bit de más peso. La tabla 2.7 muestra ejemplos de la codificación en signo y magnitud.
Tabla 2.7. Ejemplo de codificación de enteros en signo y magnitud
| Número en decimal | Signo | Valor absoluto | Signo y magnitud |
|---|---|---|---|
| -342 | - = 1 | 342 = 101010110 | 1101010110 |
| 342 | + = 0 | 342 = 101010110 | 0101010110 |
| -23 | - = 1 | 23 = 10111 | 110111 |
Si se utiliza una codificación de números enteros mediante signo y magnitud de n bits, se representan los enteros en el intervalo [-2n-1-1,2n-1-1]. Esta expresión se deriva de que el mayor número posible es aquel que comienza por un cero seguido de unos y que corresponde precisamente con el valor 2n-1-1. Análogamente, el menor número representado es el que tiene todos los dígitos a 1 y corresponde con el anterior límite, pero negativo. La figura 2.1 ilustra este rango para una representación con 8 bits sobre la recta que de números enteros.
Pero esta técnica de codificación tiene una propiedad no deseada. Con n bits se pueden representar 2n símbolos, pero si se realizan las operaciones, con la codificación de signo y magnitud, se representan 2n - 1. El problema reside en la codificación del número cero, pues es un número que no tiene signo, y por tanto la representación formada por sólo ceros y la formada por ceros con un uno a la izquierda son equivalentes.
Esto quiere decir que un elemento se representa por dos combinaciones de bits, con lo que se está desperdiciando la codificación de un número adicional. Exista una codificación alternativa a signo y magnitud que no tiene esta anomalía y se denomina “complemento a dos”.
La codificación en complemento permite codificar 2n números enteros consecutivos utilizando n bits. Más concretamente, el rango de enteros representado por n bits es [-(2n-1), 2n-1 - 1]. La figura 2.2 muestra un ejemplo de codificación de enteros en complemento a 2 con 8 bits. El código con ocho unos representa el número -1.
Esta codificación tiene múltiples propiedades que la hacen muy eficiente. El problema de la doble codificación para el número cero presente en la codificación con signo y magnitud no está presente en complemento a dos. El cero tiene una única representación y corresponde con su valor en base 2. El bit de la izquierda o más significativo sigue representando el signo del número con idéntica codificación que en el caso de signo y magnitud, los números positivos tienen este bit a cero y los negativos a uno. Los números positivos se codifican de forma idéntica a los números naturales, es decir, con su codificación en base 2.
Pero la propiedad más interesante de esta codificación es que las operaciones de suma y resta de números en complemento a dos siguen exactamente las mismas reglas que los números codificados en binario. Esta propiedad tiene una importancia enorme en el contexto de los circuitos digitales puesto que si se implementa un circuito que calcula la suma y resta de números naturales, dicho circuito se puede utilizar sin modificación alguna para sumar y restar enteros representados en complemento a 2.
La traducción de un número entero en base 10 a su representación con n bits en complemento a 2 se realiza mediante las siguientes reglas:
Si el número mayor o igual que cero, su representación corresponde es directamente su traducción a base 2 con n bits.
Si el número es negativo, su representación se obtiene mediante tres operaciones:
Obtener la representación del valor absoluto del número.
Reemplazar cada cero por un uno y cada uno por un cero. A esta operación también se le conoce como “negar” el número.
Sumar el valor 1 al número obtenido.
Por ejemplo, para calcular la representación del número -115 en complemento a dos con 8 bits, primero se calcula la representación en base dos con ocho bits del su valor absoluto 115, que es 01110011 (o su equivalente en hexadecimal 0x73). A continuación se niega el número y se obtiene 10001100. Finalmente, se suma 1 al número y se obtiene 10001101.
La traducción de un número N en complemento a dos con n bits a su representación en base 10 se realiza mediante las siguientes reglas:
Si el número N es positivo, es decir, el bit de más peso es cero, el número en base 10 se obtiene igual que en el caso de los números naturales.
Si el número N es negativo, es decir, el bit de más peso es uno, el número en base 10 se obtiene mediante la fórmula
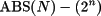
donde ABS(N) representa el número en base 10 que se obtiene al interpretar los bits en N como un número natural.
Por ejemplo, considérese el cálculo del valor en base 10 del número en complemento a dos de ocho bits 10110110. Como el bit de más peso es 1, el número es negativo. Su valor en base 10 es, por tanto
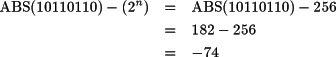
La tabla 2.8 muestra la equivalencia entre las representaciones en base dos y en decimal de los números naturales y los enteros en complemento a dos.
Tabla 2.8. Representación de números naturales y enteros en binario con n bits
| Números | Representación en base 10 |
|---|---|
|
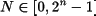
|
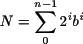
|
|
Enteros positivos.
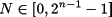
|
N empieza por cero
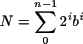
|
|
Enteros negativos.
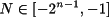
|
N empieza por uno.
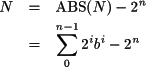
|
Si se precisa cambiar el número de bits con el que representar un número en complemento a dos, la operación no es idéntica al caso de los números naturales. Un número natural en binario no cambia si se le añaden ceros a la izquierda. Los enteros positivos representados en complemento a dos conservan esta regla. Sin embargo, la extensión de un número negativo representado en complemento requiere una operación diferente.
Los números negativos en complemento a 2 tiene su bit más significativo a uno, por tanto, para aumentar el número de bits no se pueden añadir ceros. En complemento a dos, todo número negativo mantiene su valor si se le añaden unos a la izquierda del bit de más peso. En otras palabras, para extender la representación de un número en complemento a dos basta con extender el valor que tenga como bit más significativo. A esta operación se le conoce con el nombre de “extensión de signo”.
La codificación de números reales utilizando lógica binaria es significativamente más compleja que el caso de los naturales o enteros. Parte de esta complejidad deriva del hecho de que si bien al utilizar un número finito de bits se representaba un intervalo concreto de números enteros o naturales, en el caso de los números reales esta técnica no es posible.
Dado que entre dos números reales existe un número infinito de números, no es posible representar todos los números en un intervalo concreto sino que se representan únicamente un subconjunto de los números contenidos en dicho intervalo. Esta propiedad plantea un inconveniente que debe ser tenido en cuenta no sólo en el diseño de los circuitos digitales capaces de procesar números reales, sino incluso en los programas que utilizan este tipo de números.
Supóngase que se operan dos números reales representados de forma binaria y que el resultado no corresponde con uno de los números que pueden ser representados. Esta situación es perfectamente posible dado que entre dos números hay infinitos números reales. La única solución posible en lógica digital consiste en representar este resultado por el número real más próximo en la codificación. La consecuencia inmediata es que se ha introducido un error en la representación de este resultado. En general, cualquier número real fruto de una operación tiene potencialmente el mismo problema. En algunos casos este error no existe porque el número sí puede ser representado de forma digital, pero en general, la manipulación de números reales puede introducir un error.
Este posible error introducido por la representación adquiere especial relevancia en aquellos programas que realizan cálculos masivos con números reales. Existen técnicas de programación orientadas a minimizar el error producido cuando se manipulan números.
Los números reales se codifican en lógica binaria mediante la técnica conocida como “mantisa y exponente” que está basada en la siguiente observación: todo número real consta de una parte entera y una parte decimal. La parte entera es aquella a la izquierda de la coma, y la parte decimal a la derecha. A esta parte decimal se le denomina “mantisa”. En el contexto de los números reales, la multiplicación y división por potencias de la base es equivalente al desplazamiento de la coma a lo largo de los diferentes dígitos que conforman el número. Una multiplicación por una potencia positiva de la base implica un desplazamiento de la coma a la derecha, y de forma análoga, la multiplicación por una potencia negativa de la base es equivalente a un desplazamiento de la coma a la izquierda. El ejemplo 2.2 muestra esta equivalencia para los números reales en base 10.
Mediante operaciones de multiplicación y división por la base es posible representar todo número real por una mantisa en la que el primer dígito significativo está a la derecha de la coma multiplicado por una cierta potencia de la base. La ventaja de la representación en coma flotante respecto a la representación en coma fija es que permite representar números muy pequeños o muy grandes de forma muy compacta. El número 0.1*10-10 necesita 11 dígitos para representarse en punto fijo, sin embargo, en coma flotante utilizando base 10 tan sólo se precisa representar la mantisa 0.1 y el exponente -10.
La representación de los números reales positivos en base 2 sigue las mismas reglas que la representación de los naturales en lo que respecta al peso de cada uno de sus dígitos. El peso de los bits de la parte decimal se obtiene multiplicando por 2 elevado a su posición pero con exponente negativo. Por ejemplo:
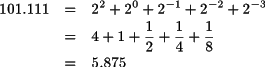
La notación de mantisa y exponente se puede aplicar de forma análoga a números codificados en base 2. En este caso las potencias utilizadas en la multiplicación son potencias de 2. El ejemplo 2.3 muestra esta equivalencia en la representación binaria.
Los números reales, por tanto, se representan tal que su primera cifra significativa en la mantisa sea aquella que está a la derecha de la coma y se multiplica por la potencia pertinente de la base. La codificación de los números reales en base 2 consta de tres partes: la mantisa, su signo y el exponente. La base sobre la que se aplica el exponente está implícita en la representación, y es la base 2.
El bit de signo hace referencia al signo de la mantisa y se mantiene la misma convención que en el caso de la codificación de enteros como signo y magnitud (ver sección 2.6), el signo positivo se representa como 0 y el negativo como 1.
La mantisa representa la parte decimal del número y tiene una influencia directa sobre su precisión. Cuantos más bits se incluyan en la mantisa, mayor precisión tendrá la codificación. Tiene sentido hablar de “precisión” de la representación porque se está considerando un subconjunto de todos los números reales posibles.
Para la mantisa se aplica una mejora que permite el incremento de la precisión. Como esta se obtiene desplazando el número hasta que el primer dígito significativo esté a la derecha de la coma, en base 2, esto quiere decir que dicho dígito siempre es un uno y por tanto no es preciso almacenarlo. Por tanto, si una representación de números reales utiliza 23 bits para la mantisa, en realidad está representando 24 bits, pues el primero es siempre 1. A esta técnica se le conoce con el nombre de “bit escondido”.
El exponente es un número entero y por tanto se puede utilizar cualquiera de las técnicas de codificación presentadas anteriormente. La más común es complemento a 2. La figura 2.3 muestra la estructura de la representación binaria de un número real en coma flotante.
En este tipo de codificación no basta con saber el tamaño en bits de su representación, sino que es preciso especificar además, cuántos bits se utilizan para codificar la mantisa y el exponente (el signo siempre se codifica con un bit).
Al igual que en el caso de los números naturales y enteros, cuando un número está fuera del rango de representación, se produce un de desbordamiento, pero en el caso de los números reales, esta situación es más compleja. Aparte del problema de representación de números mayores al rango posible, también aparece un problema cuando el valor absoluto de un número es demasiado pequeño.
Por ejemplo, supóngase que el valor más pequeño diferente de cero que se puede representar mediante coma flotante es n. Al dividir dicho número por 3, la representación debe escoger el número real más próximo que pueda ser representado, que en este caso es el cero.
Pero que un número diferente de cero se represente como cero tiene efectos muy significativos en los cálculos. Por ejemplo, si el número que ha producido el resultado cero se multiplica por cualquier otro factor, el resultado es cero, y por tanto incorrecto. En realidad, la propiedad que hace esta situación tan delicada es que, en adelante, no hay forma de acotar el error producido por la representación en coma flotante. A esta situación se le conoce con el nombre de “desbordamiento por abajo” o underflow.
Las situaciones de desbordamiento al operar números en coma flotante suelen producir excepciones en la ejecución de un programa que pueden ser procesadas por los propios programas para recuperarse, o bien producen la terminación abrupta de su ejecución.
La representación de números reales en coma flotante puede seguir diferentes estrategias dependiendo del número de bits para codificar mantisa y exponente, tipo de codificación del exponente, cómo se tratan condiciones especiales como desbordamiento, etc.
El Instituto de Ingeniería Eléctrica y Electrónica (en adelante IEEE) ha propuesto dos estándares para la representación de números reales, el IEEE 754 y el IEEE 854, de los cuales, el más utilizado es el IEEE 754. Esta representación tiene cuatro posibles precisiones: precisión simple, simple extendida, precisión doble, y doble extendida. La tabla 2.9 muestra las características de cada una de ellas. Nótese que en algunos de los parámetros, el estándar tan sólo especifica una cota, y no un valor fijo.
Tabla 2.9. Parámetros del formato IEEE 754
| Parámetro | Simple | Simple Extendida | Doble | Doble Extendida |
|---|---|---|---|---|
| bits de la mantisa | 24 | 32 | 53 | 64 |
| máximo exponente | 127 | 1023 | 1023 | ≥16383 |
| mínimo exponente | -126 | ≤-1022 | 1022 | ≤16382 |
| bits del exponente | 8 | ≤11 | 11 | 15 |
| tamaño total | 32 | 43 | 64 | 79 |
La mantisa se representa utilizando la codificación de signo y magnitud y aplicando la técnica de bit escondido. Por ejemplo, en la precisión simple se utiliza un bit para el signo y 24 para la magnitud. En el bit de signo el 0 representa el signo positivo y el 1 el negativo.
Los exponentes son números enteros su valor se representa utilizando un esquema de desplazamiento o suma de una constante que para la precisión simple es 127 y para la doble es 1023. El valor real del exponente se obtiene restando la constante pertinente de su interpretación en base 2.. Por ejemplo, en la precisión simple del formato, si el exponente contiene el número 23, corresponde con el exponente 23 - 127 = -104 y en precisión doble con 23 - 1023 = -1000. Los exponentes con valores todo ceros o todo unos están reservados para situaciones excepcionales.
Los rangos resultantes de estas representaciones difieren significativamente de los obtenidos en las representaciones de enteros y naturales. A igual número de bits, la representación en coma flotante cubre un rango más extenso de números pero a condición de representar sólo un subconjunto de ellos. La tabla 2.10 muestra los rangos de representación de las precisiones simple y doble.
Tabla 2.10. Rangos representados en los formatos simple y doble
| Precisión | Negativos | Positivos |
|---|---|---|
| Simple |
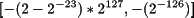
|
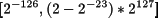
|
| Doble |
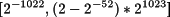
|
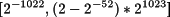
|
Para el caso concreto de la precisión simple, hay cinco rangos numéricos que son imposibles de representar.
Números negativos menores que -(2-2-23)*2127. Producen un desbordamiento negativo.
Números negativos mayores que -2-126. Producen un desbordamiento por abajo.
El número cero
Números positivos menores que 2-126. Producen un desbordamiento por abajo.
Números positivos mayores que (2-2-23)*2127. Producen un desbordamiento positivo.
El número cero no puede ser representado con este esquema debido a la utilización de la técnica del bit escondido. Para solventar este problema se le asigna un código especial en el que tanto la mantisa como el exponente tienen todos sus bits a cero y el bit de signo es indeterminado (con lo que el cero tiene dos posibles representaciones).
Otros dos valores a los que se les asigna un código especial son +∞ y -∞ que se codifican con el pertinente bit de signo, el exponente con todo unos y la mantisa con todo ceros.
Otro caso especial a considerar con esta codificación es cuando se produce un resultado que es imposible de representar. Para esta situación se utiliza la notación “NaN” (acrónimo de Not a Number). Estos valores a su vez se dividen en dos categorías dependiendo si el resultado es indeterminado o inválido y se denotan respectivamente por los símbolos “QNaN” y “SNaN”. En ambos casos el exponente tiene todos sus bits a uno y la mantisa es diferente de cero. El valor de la mantisa se utiliza para distinguir entre las dos posibles situaciones.
Aparte de manipular números, un procesador debe poder representar y manipular conjuntos arbitrarios de símbolos. Al igual que en el caso de los números, la lógica digital fuerza a que dichos símbolos se codifiquen con bits pero, a diferencia de los números, un conjunto de símbolos arbitrario no tiene un conjunto de operaciones específicas que se realizan sobre él.
La definición de una codificación de un conjunto de símbolos precisa tres datos:
el conjunto de símbolos,
el número de bits a utilizar en la codificación,
la correspondencia entre cada símbolo del conjunto y la secuencia de bits que lo representa.
El número de bits a utilizar tiene la restricción derivada de la ecuación 2.1. Con n bits se pueden codificar un máximo de 2n elementos, por tanto, si se denota por C la cardinalidad del conjunto de símbolos se debe cumplir la ecuación 2.6.
Por ejemplo, se dispone del conjunto de símbolos para codificar S = { Rojo, Verde, Azul }. Se decide utilizar el mínimo número de bits para su codificación, en este caso 2. La correspondencia entre los símbolos y su codificación se establece mediante la siguiente tabla
| Símbolo | Codificación |
|---|---|
| Rojo | 00 |
| Verde | 01 |
| Azul | 10 |
Como la cardinalidad del conjunto no es una potencia de dos, existen más combinaciones de bits que elementos lo que permite que existan múltiples posibles correspondencias.
Uno de los conjuntos de símbolos que más se utilizan en un procesador son aquellos que se introducen a través del teclado. Desde la aparición de los primeros procesadores ha existido la necesidad de tener una codificación para estos símbolos. Además, dado que los ordenadores intercambian entre sí infinidad de datos, esta codificación es deseable que sea idéntica para todos ellos.
Una de las codificaciones de letras que más trascendencia ha tenido en los últimos años es la codificación ASCII (American Standard Code for Information Interchange). En ella se incluyen so sólo letras y dígitos, sino también códigos especiales para la transmisión de mensajes a través de teletipos. El tamaño de la representación es de 8 bits y por tanto, el número máximo de símbolos que puede codificar es 256
El código contiene en sus primeras 32 combinaciones (de la 00000000 a
la 0100000) un conjunto de símbolos que no son imprimibles y que se
utilizaban para la transmisión de texto entre dispositivos. Los
símbolos con códigos del 33 al 127 son los que sí pueden
imprimirse. Por ejemplo, el espacio en blanco se codifica como
0x20. Las letras del la “a” a la
“z” ocupan los códigos del 0x61 al
0x7A (en este rango no está incluida la ñ). Sus
correspondientes símbolos en mayúsculas ocupan los códigos del
0x41 al 0x5A (la diferencia numérica entre
los códigos de mayúscula y minúscula es idéntica).
Pero el código ASCII no fue el único utilizado para representar letras, sino que ha convivido con otras alternativas similares tales como EBCDIC (Extended Binary Coded Decimal Interchange Code) que aun se utilizan en algunos de los ordenadores actuales.
Una de las carencias más importantes del código ASCII es la ausencia de codificación para los símbolos que no son parte del alfabeto anglosajón, como por ejemplo, todas las letras que incluyen tildes, diéresis, etc. Para dar cabida a estos símbolos se definió lo que se conoce como el código ASCII extendido que incluye en los valores del 128 al 255 estos símbolos así como un conjunto de símbolos gráficos y matemáticos.
Esta extensión, a pesar de dar cabida a algunos de los alfabetos utilizados en países de habla no inglesa, no fue suficiente para incorporar alfabetos tales como los asiáticos o los de oriente medio que constan de un número muy elevado de grafías.
La única solución posible ha sido proponer una nueva codificación con el tamaño suficiente para dar cabida a todos los alfabetos existentes. Con tal motivación se diseño la codificación “Unicode” cuyo objetivo es proveer una única representación numérica para cada símbolo independientemente de la plataforma, el programa o el lenguaje en el que se manipule.
La codificación Unicode se ha transformado en un estándar adoptado por las principales empresas de hardware y software. Su presencia no cubre la totalidad de aplicaciones, pero con el paso del tiempo será la única representación utilizada.
El estándar pretende ser lo más genérico posible, y por tanto, en lugar de fijar un único tamaño para la representación, su codificación la divide en tres posibles formas: 8 bits, 16 bits y 32 bits. Estas codificaciones son diferentes pero todas son parte del estándar y se conocen con los nombres de “UTF-8”, “UTF-16” y “UTF-32” respectivamente. La correspondencia entre la representación numérica y los símbolos está perfectamente definida y tabulada en cada una de los tres formatos. La tabla 2.11 muestra un ejemplo de tres símbolos y su codificación en Unicode.
Tabla 2.11. Ejemplo de símbolos codificados con Unicode
| Imagen | Símbolo | Código |
|---|---|---|
| z | z minúscula | 0x007A |
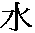
|
agua en chino | 0x6C34 |
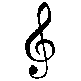
|
clave de sol |
0xD834 0xDD1E
|
Una vez definida la codificación de todas las letras y símbolos adicionales, las cadenas de estos símbolos se representan mediante una secuencia de estos códigos en los que cada número corresponde con una letra. Esta codificación es la utilizada por los editores de texto plano para la representación interna del texto. Algunos de ellos incluso permiten cambiar la codificación utilizada entre ASCII y alguno de los formatos Unicode. La tabla 2.12 muestra el texto de un programa en lenguaje ensamblador y su representación equivalente utilizando el código ASCII (los valores numéricos están en hexadecimal).
Tabla 2.12. Texto de un programa y su codificación en ASCII
| Texto |
.data
msg: .asciz "Hello world\n"
.text
.globl start
main: push $msg
call printf
add 4, %esp
ret
|
| Codificación ASCII |
20 20 20 20 20 20 2E 64 61 74 61 0A 6D 73 67 3A 20 20 2E 61 73 63 69 7A 20 22 48 65 6C 6C... 20 20 20 20 20 20 2E 74 65 78 74 0A 20 20 20 20 20 20 2E 67 6C 6F 62 6C 20 73 74 61 72 74... 6D 61 69 6E 3A 20 70 75 73 68 20 24 6D 73 67 0A 20 20 20 20 20 20 63 61 6C 6C 20 70 72 69 6E 74 66 0A 20 20 20 20 20 20 61 64 64 20 24 34 2C 20 25 65 73 70.... 20 20 20 20 20 20 72 65 74 0A |
Una de las codificaciones más importante que necesita un procesador es el de su propio conjunto de instrucciones. En él, cada posible instrucción con sus operandos se considera un elemento. Para su codificación es preciso escoger tanto el número de bits como la correspondencia entre instrucciones y su codificación binaria.
Para ilustrar este tipo de codificación se utilizará un conjunto inicial de instrucciones sencillas a modo de ejemplo en el que se irán incorporando de forma gradual más elementos para ver cómo la codificación puede ser adaptada. El conjunto inicial de instrucciones se denota por el nombre “ual-1”.
En lugar de definir el conjunto de instrucciones mediante una simple
enumeración de todos sus elementos, se divide la instrucción en partes
y se proponen codificaciones separadas para los valores de cada una de
las partes. Las instrucciones del conjunto ual-1 constan de tres
partes: una operación y dos operandos que son dos números reales en el
rango 0 a 255. El código de operación puede tener uno de los siguientes
cuatro valores: add, sub, mul y
div. La figura 2.4 muestra la
estructura de las instrucciones que conforman este conjunto de
símbolos así como varias instrucciones de ejemplo.
El primer paso para diseñar una codificación es calcular el número de elementos que contiene ual-1. La primera parte tiene 22 posibles valores, la segunda 28 y la tercera igualmente 28 posibles valores. Todas las combinaciones son posibles, por tanto el número de elementos se obtiene multiplicando estos factores:
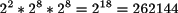
El número de bits y la cardinalidad deben satisfacer la ecuación 2.6 y por tanto se precisan al menos 18 bits. En lugar de utilizar el número mínimo de bits, se decide utilizar el menor múltiplo de 8 bits, es decir, 24 bits (3 bytes).
La correspondencia entre los símbolos y su representación en binario se establece igualmente de forma implícita para evitar la enumeración de todos los elementos. Las reglas de esta codificación son:
El código de operación se codifica con dos bits y la siguiente correspondencia:
| Símbolo | Codificación |
|---|---|
add |
00 |
sub |
01 |
mul |
10 |
div |
11 |
El segundo y tercer operandos se codifican con su representación en base 2.
Toda codificación se escribe de izquierda a derecha, y se completa con 6 dígitos consecutivos con valor 0 para obtener un total de 24 bits.
La figura 2.5 ilustra el formato de la codificación binaria de los elementos de ual-1.
Siguiendo esta codificación, la instrucción que representa la suma de
los números 0x27 y 0xB2, representada por
ADD 0x27 0xB2, se codifica en binario tal y como se
ilustra en la figura 2.6. La secuencia
de 24 bits resultante se codifica en base hexadecimal para reducir su
tamaño y facilitar su manipulación.
La propiedad más importante de esta codificación es que la traducción de cualquier instrucción a su representación en binario y viceversa es un proceso sistemático.. La tabla 2.13 muestra la codificación de otros símbolos del conjunto ual-1.
Tabla 2.13. Representación en hexadecimal de símbolos de ual-1
| Símbolo | Codificación |
|---|---|
| ADD 0x27 0xB2 | 0x09EC80 |
| SUB 0x11 0x2F | 0x444BC0 |
| MUL 0xFA 0x2B | 0xBE8AC0 |
| DIV 0x10 0x02 | 0xC40080 |
En general, el número hexadecimal resultante no contiene los mismos dígitos que en el símbolo del que procede. Esto sucede porque los bits son reorganizados e interpretados de forma diferente, pero la información sigue estando contenida en el resultado.
A continuación se define un nuevo conjunto de símbolos derivado de
ual-1 pero con una estructura más compleja. Se añade a cada símbolo un
cuarto elemento que define el lugar donde almacenar el resultado de la
operación y que puede tener los valores LugarA o
LugarB. Este nuevo conjunto se denotará por
ual-2. La estructura de los símbolos de ual-2 así como
ejemplos de algunos de sus símbolos se muestra en la figura 2.7.
Tras definir el nuevo conjunto, se obtiene el número de elementos de
los que consta. De cada elemento del conjunto ual-1 se obtienen dos
elementos del nuevo conjunto ual-2: uno con el sufijo
LugarA y otro con el sufijo LugarB. Por
tanto, el número de elementos de ual-2 es
219 y se requieren al menos 19 bits para su
codificación. Al igual que en el caso de ual-1, la representación se
realiza en múltiplos de bytes, y por tanto se utilizarán 24 bits.
La correspondencia entre los elementos de ual-2 y su representación binaria sigue las mismas reglas que para el caso de ual-1 con la modificación de que el operando añadido se codifica con un único bit y según la codificación que se muestra en la tabla 2.14.
La nueva codificación utiliza 19 bits en lugar de los 18 anteriores y con la estructura que se ilustra en la figura 2.8.
El proceso de traducción de símbolo a su representación con seis dígitos hexadecimales y viceversa se puede hacer igualmente de forma sistemática. La tabla 2.15 muestra varios ejemplos de representación de símbolos de ual-2 en binario y hexadecimal.
Tabla 2.15. Representación en binario y hexadecimal de símbolos de ual-2
| Símbolo | Binario | Hexadecimal |
|---|---|---|
div 0x10 0x02 LugarA |
11 0001 0000 0000 0010 0 00000 |
0xC40080 |
add 0x10 0x02 LugarB |
00 0001 0000 0000 0010 1 00000 |
0x0400A0 |
mul 0x10 0x02 LugarA |
10 0001 0000 0000 0010 0 00000 |
0x840080 |
Al proceso de traducción de un símbolo del conjunto ual-2 a su equivalente en binario (o hexadecimal) se denominará “codificación”, y al proceso inverso por el que se obtiene un símbolo a partir de su codificación en binario se denominará “decodificación”. Dadas la reglas de traducción, estos dos procesos se pueden realizar de forma automática.
La decodificación de instrucciones es precisamente lo que realiza un procesador cuando recibe una instrucción a ejecutar. Al igual que el resto de datos que manipula, las instrucciones están codificadas como secuencias binarias. Una vez recibida se decodifica para saber qué cálculo se debe realizar.
Los dos esquemas de codificación de los conjuntos ual-1 y ual-2 tienen múltiples decisiones arbitraras: la correspondencia de las operaciones con sus códigos de dos bits, el orden en el que se concatenan los códigos binarios, el número total de bits a utilizar en la representación (mientras se respete el mínimo), la colocación de los bits de relleno, etc. Estas decisiones pueden ser modificadas dando lugar a codificaciones diferentes pero igualmente válidas. La propiedad que se debe mantener es la posibilidad de codificar y decodificar los símbolos de forma inequívoca.
Los bits de relleno añadidos a la derecha para alcanzar el tamaño de 24 bits ofrecen cierto grado de ambigüedad. Dados dos números binarios de 24 dígitos, si la única diferencia entre ellos radica en los bits de rellenos, al interpretarse como símbolos de ual-1 o ual-2, ambos corresponden con el mismo símbolo. Esta propiedad no cambia en nada el proceso de codificación y decodificación, tan sólo pone de relieve el hecho de que el número de bits utilizado permite más combinaciones que número de elementos hay en el conjunto.
A continuación se define un nuevo conjunto, que se denotará por
“ual-3” y en el que en los dos primeros operandos que
hasta ahora sólo podía haber un número de ocho bits, ahora se permite o
un número de ocho bits, o un lugar con valores LugarA o
LugarB. Este nuevo conjunto extiende al conjunto ual-2 con
aquellos símbolos en los que la segunda o tercera parte representa un
lugar. Se puede comprobar que ual-2 es un subconjunto de ual-3.
Este nuevo conjunto representa aquellas instrucciones cuyos operandos
no sólo son valores numéricos sino que pueden contener uno de los dos
posibles lugares LugarA o LugarB no sólo para
almacenar el resultado (como indica el último campo de la instrucción)
sino como lugar de donde obtener un operando. Por ejemplo, el símbolo
ADD LugarA 0x10 LugarB forma parte del nuevo conjunto
ual-3 y podría representar la orden por la cual se obtiene el contenido
de LugarA, se suma 0x10 y el resultado se
almacena en LugarB.
La cardinalidad de este nuevo conjunto se calcula multiplicando el número de combinaciones posibles que tiene cada una de las partes de la instrucción. El código de operación sigue teniendo cuatro posibles valores, pero ahora cada uno de los operandos tiene los 256 posibles valores del número natural más dos posibles valores que representan un lugar. Por tanto el número de elementos de ual-3 es:
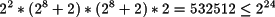
Siguiendo la política utilizada hasta ahora, el tamaño de la codificación se realiza en múltiplos de bytes, y por tanto, ocupa 24 bits que siguen siendo suficientes. La correspondencia entre símbolos y su codificación binaria necesita ser revisada, pues ahora los valores posibles de los operandos superan los 256 que se codificaban con ocho bits. Se precisa un esquema que permita codificar los 258 posibles valores de cada uno de los operandos y para ellos se precisan al menos 9 bits, puesto que 258 > 28.
La codificación con 9 bits ofrece 512 combinaciones, mientras que tan
sólo existen 258 posibles valores a codificar. Una posible solución
consiste en dividir los 9 bits en dos grupos de 1 y 8 bits. Si el
primer bit es cero indica que en los siguientes 8 se codifica un número
natural entre 0 y 255. Si es uno indica que se codifica uno de los dos
valores LugarA o LugarB. En el primer caso se
utilizan todos los bits, mientras que en el segundo, el lugar se
codifica en el último de los ocho bits ignorando el valor de los 7 bits
restantes. La figura 2.9 ilustra este
esquema de codificación.
Al haber menos elementos (258) que codificaciones posibles con 9 bits (512), aparecen numerosas combinaciones que codifican el mismo operando. Concretamente, cuando se codifica un lugar, aquellas combinaciones con un uno en el primer bit, un determinado valor en el último y cualquier combinación en los siete bits restantes representan el mismo operando. La tabla 2.16 muestra ejemplos de la codificación de operandos en ual-3.
Tabla 2.16. Ejemplos de codificación de operandos en ual-3
| Codificación binaria | Operando |
000010010 |
0x12 |
100010011 |
LugarB |
001111010 |
0x7A |
100010010 |
LugarA |
1XXXXXXX0 |
LugarA |
Tal y como se muestra en la última fila de la tabla 2.16, cuando el valor de un bit en una secuencia no es relevante, se suele representar por el valor “X”.
Al aplicar la nueva correspondencia, el código binario resultante consta de siete partes: la operación, el bit que indica el tipo de primer operando, el primer operando, el bit de tipo del segundo operando, el segundo operando, el tercer operando y los bits de relleno. La figura 2.10 muestra esta estructura.
La tabla 2.17 muestra ejemplos de codificación de instrucciones del conjunto ual-3.
Tabla 2.17. Codificación de instrucciones de ual-3
| Instrucción | Binario |
add 0x01 0x00 LugarA |
0x002000 |
add 0x02 0x00 LugarB |
0x004008 |
mul LugarB 0x03 LugarA |
0xA02030 |
mul LugarB 0x04 LugarA |
0xA02040 |
Los esquemas de codificación como el mostrado hasta ahora son una simplificación de los utilizados para que un procesador sepa qué instrucción debe ejecutar. Desde que el procesador recibe el voltaje necesario para funcionar, hasta que dicho voltaje desaparece, la única tarea que se realiza es la obtención de un conjunto de bits, su interpretación, la ejecución de la instrucción pertinente y la obtención del siguiente conjunto de bits.
La codificación de una secuencia de instrucciones se transforma en una secuencia de códigos binarios, cada uno de los cuales codifica una instrucción y que el procesador carga una tras otra y las ejecuta. El lugar donde deben están almacenados estos valores es la memoria RAM que se comparte con el almacenamiento de los datos.
El número de bits utilizado para codificar un conjunto de símbolos influye directamente en la cantidad de memoria necesaria para almacenar una secuencia de instrucciones. Cuanto más compacta sea la representación menor cantidad de memoria se utiliza y más cantidad de información se puede almacenar, por lo que este es un criterio que se tiene en cuenta a la hora de diseñar la codificación del lenguaje de un procesador.
A la vista del esquema de codificación utilizado para ual-3 cabe preguntarse: ¿es posible codificar las instrucciones utilizando un número menor de bits para utilizar menos cantidad de memoria? En un primer análisis se puede comprobar que si la instrucción tiene como sus dos primeros operandos dos números de 8 bits, la codificación no puede ser reducida, pues cada uno de los bits tiene un cometido.
Sin embargo, en el caso de que alguno de los dos primeros operandos contenga un lugar, parte de los bits no se utilizan, por lo que se puede considerar un esquema de representación más compacto. Se propone un nuevo esquema en el que la codificación del primer y segundo operando se modifica de la siguiente forma:
Si el operando es un número de ocho bits se mantiene la codificación anterior con un bit de prefijo con valor 0.
Si el operando es un lugar, se codifica con dos bits, el primero tiene valor 1 y el segundo codifica el lugar.
Con este nuevo esquema de codificación, el símbolo add LugarB
0x10 LugarB se codifica con la secuencia de 14 bits 00 11 0 0001
0000 1. Si se asume que la representación se debe hacer en múltiplos de
bytes, se añaden dos bits de relleno al final para un total de 16 bits
o dos bytes: 0x3084.
La pregunta que cabe hacerse ahora es ¿mantiene esta representación la propiedad de ser una codificación sistemática? La respuesta es que sí pero con una modificación sustancial. El proceso de codificación queda perfectamente definido por las reglas anteriormente enunciadas. El proceso de decodificación sí requiere una estrategia diferente a las anteriores puesto que como el tamaño de la codificación es variable, su interpretación se debe realizar de forma incremental.
Los pasos a seguir consisten en obtener un primer byte y analizar los
bits en orden para ver qué codifican. Dependiendo de los valores
presentes se obtienen más o menos bits para decodificar los valores de
los operandos. Así, por ejemplo, con la representación
0x3084 se observa que los dos primeros bits son cero,
representando la operación add y que el siguiente bit es
un uno, por lo que en lugar de obtener los ocho siguientes tan sólo se
obtiene el siguiente que ahora sí se sabe que codifica uno de los dos
lugares. A continuación se procesan los bits restantes. El siguiente es
un cero, con lo que es preciso procesar los ocho bits siguientes, y
acceder al siguiente byte. Una vez obtenidos los campos se concluye que
no se necesitan más bytes y se obtiene el símbolo pertinente.
Este esquema de codificación mantiene tanto la propiedad de ser sistemático y como la premisa de representar las instrucciones con tamaños que sean múltiplos de bytes. A cambio resultan instrucciones de uno, dos y tres bytes dependiendo de los operandos que contengan.
Este último ejemplo ilustra las dos categorías en las que se dividen los lenguajes máquina de los procesadores comerciales ateniéndose a la longitud de su codificación: formato fijo y formato variable.
Formato fijo: todas las instrucciones del lenguaje máquina tienen la misma longitud. Generalmente se dividen en porciones y cada porción codifica un elemento de la instrucción. Como principal ventaja ofrecen una decodificación muy rápida, pues las reglas son muy simples. Como principal desventaja se desperdicia memoria al almacenarlas, pues algunos de los campos en algunas instrucciones no son necesarios.
Formato variable: las instrucciones tienen tamaño diferente dependiendo de la información que contienen. Como principal ventaja ofrece una representación muy compacta del código y por necesita menos memoria para ser almacenada. Como inconveniente, el proceso de decodificación de una instrucción requiere múltiples pasos así como un acceso gradual a la secuencia de bits.
La complejidad del proceso de decodificación de una instrucción por el procesador tiene un impacto significativo en su velocidad de proceso. Esta fase es común a todas las instrucciones, y por tanto, si el proceso es demasiado lento, acaba afectando a la velocidad global de ejecución. En la actualidad, estas dos categorías están presentes en el panorama de procesadores.
La codificación de un lenguaje máquina implica un proceso de decodificación que se realiza en el procesador, y que por tanto debe ser implementado como un circuito digital. Pero para poder escribir programas en ese lenguaje máquina se precisa una descripción detallada de cada una de las instrucciones así como las reglas que permiten su codificación en binario.
Toda descripción de un lenguaje máquina suele ir precedida por una descripción de la arquitectura del procesador que lo ejecuta. Esto es así porque en dicho lenguaje se permite la referencia a los elementos del procesador que se ofrecen para su programación. Tras la descripción de la arquitectura, la forma de describir el lenguaje máquina es agrupando sus operaciones. En lugar de describir todas las instrucciones posibles con todas las posibles combinaciones de operandos, se suelen describir juntas todas aquellas que tienen una funcionalidad similar. El apéndice A contiene la descripción del subconjunto de instrucciones máquina del Intel Pentium que serán consideradas a lo largo de este documento.
Todo procesador incluye, como parte de su definición, un conjunto de documentos con una descripción detallada de su arquitectura, del entorno de programación, de todas y cada una de sus instrucciones, así como de los mecanismos auxiliares que se ofrecen para facilitar la ejecución de programas de usuario y del sistema operativo.
¿Cuántos bits se precisan para codificar 34 elementos? ¿y 32? ¿Se pueden codificar en binario 34 elementos con 8 bits?
¿A partir de qué número de elementos se tienen que utilizar al menos 8 bits para su codificación binaria?
Escribir sin utilizar la calculadora las potencias de 2 hasta 216. ¿Qué representa cada uno de esos números?
Utilizando únicamente los datos que aparecen en esta tabla y sin realizar operación aritmética alguna, ¿se pueden codificar 5642 elementos con 13 bits?
De los siguientes números, dos de ellos están escritos incorrectamente, ¿cuáles son? ¿por qué?
100110
10032
5007
5034
5556
Calcular el equivalente en base 10 de los siguientes números:
437
11002
5346
7778
1009
Rellenar la siguiente tabla con la representación equivalente en las diferentes bases de los números en base 10 dados.
| Base 10 | Base 2 | Base 5 | Base 8 |
|---|---|---|---|
| 2910 | |||
| 43210 | |||
| 945310 |
Rellenar la siguiente tabla con la representación equivalente en base 10 o binario de los números dados.
| Binario | Decimal |
|---|---|
| 1345 | |
| 110111 | |
| 255 | |
| 101010 | |
| 4097 | |
| 100000 |
Rellenar la siguiente tabla con la representación equivalente en octal, hexadecimal o binario de los números dados.
| Binario | Octal | Hexadecimal |
|---|---|---|
| 01345 | ||
| 110111 | ||
| 0xF231 | ||
| 101010 | ||
| 04077 | ||
| 0xBACA |
La representación de un número de 12 bits en octal es 7??3. Donde “?” representa un dígito desconocido. ¿Cuáles de las siguientes representaciones de ese mismo número en hexadecimal son posibles?
0xE?3
0xE?C
0xF?3
0xF?C
¿Qué intervalo de enteros permite representar la codificación en complemento a dos con 11 bits?
Realizar las operaciones 100011-101100 y 100011 + 101100 donde los operandos son números enteros representados en complemento a 2 con 6 bits. Comprobar que los resultados obtenidos son consistentes con la representaicón en base 10 de los operandos.
Rellenar la siguiente tabla con la representación equivalente en complemento a dos con 10 bits o decimal de los siguientes números.
| Complemento a 2 | Decimal |
|---|---|
| -445 | |
| 1000110111 | |
| -511 | |
| 0111010110 | |
| -1012 | |
| 1000000000 |