| Capítulo 3. Almacenamiento de datos en memoria | ||
|---|---|---|
 |

|
|
Tabla de contenidos
En este capitulo se estudia el funcionamiento de la memoria RAM que utiliza el procesador para almacenar todos aquellos datos y código que precisa para la ejecución de un programa. También se estudia la técnica de la indirección por la que se manipulan direcciones de memoria que apuntan a datos en lugar de los propios datos.
Los circuitos digitales únicamente pueden procesar datos representados con ceros y unos, pero para ello deben estar almacenados en otro circuito que permita a su vez su modificación. En el contexto de un ordenador este dispositivo suele ser la memoria RAM (random access memory), un circuito que contiene en su interior una tabla que almacena información en cada uno de sus compartimentos.
Como toda tabla, es preciso saber dos de sus dimensiones: el tamaño de cada uno de sus elementos, y el número de elementos de los que dispone. Actualmente, las memorias convencionales almacenan la información en elementos de tamaño 1 byte. Por lo tanto una memoria se puede ver como una tabla que contiene un determinado número de bytes. Los elementos de esta tabla están numerados con números naturales comenzando por el cero. El número correspondiente a cada una de los elementos se denomina “dirección de memoria” y se suele representar de forma abreviada por el símbolo “@”. Al conjunto de números que representan las direcciones de una memoria se le denomina su “espacio de direcciones”. La figura 3.1 ilustra la estructura, contenido y direcciones de una memoria RAM.
El acceso a los datos internos de la memoria viene determinado por el tamaño de sus celdas o elementos. Tal y como está estructurada, la memoria no ofrece acceso directo a cualquiera de sus bits, sino que es preciso primero obtener un byte y posteriormente acceder al bit pertinente. Los procesadores incluyen en su lenguaje máquina las instrucciones necesarias para poder manipular los bits de un byte. Si se quiere, por tanto cambiar un bit de un byte de memoria se debe leer el byte entero, utilizar instrucciones para cambiar su valor, y escribirlo de nuevo en memoria.
Internamente la memoria está implementada por un conjunto de transistores diseñados de tal forma que pueden almacenar la información dada. La unidad responsable de almacenar un bit de información se denomina “celda”. Un chip de memoria no es más que un circuito que contiene un determinado número de celdas en cuyo interior se almacena un bit. Existen dos técnicas para el diseño de memoria: estática y dinámica.
La memoria RAM estática o SRAM es un circuito que una vez que se escribe un dato en una de sus celdas lo mantiene intacto mientras el circuito reciba voltaje. En cuanto el voltaje desaparece, también lo hace la información. La celda de dicha memoria está compuesta por alrededor de seis transistores conectados de forma similar a un registro. El tiempo de lectura de una posición de memoria compuesta por ocho celdas suele ser del orden de decenas de nanosegundos (1 nanosegundo son 10-9 segundos).
La memoria RAM dinámica o DRAM es similar a la anterior pues también almacena información, pero su estructura interna es radicalmente diferente. La celda de memoria dinámica consta únicamente de un transistor y un condensador. Este último es el que almacena una carga, mientras que el transistor se utilizar para su carga y descarga. La celda de memoria dinámica almacena el valor 1 cuando el condensador está cargado, y cero cuando está descargado. El problema que presenta esta celda es que, a pesar de estar conectada continuamente a su alimentación, si el condensador almacena el valor 1 y no se realiza ninguna operación, su carga se degrada hasta alcanzar el valor 0. Es decir, la celda de esta memoria no es capaz de mantener el valor uno durante un tiempo arbitrario, sino que acaba perdiéndose. Pero, tal y como está diseñada la lógica de lectura, al leer una celda se refresca totalmente su valor, y por tanto se recupera la pérdida de carga que pudiera haberse producido. El tiempo que tarda una celda en perder su información es del orden de milisegundos (1 milisegundo son 10-3 segundos).
Este comportamiento de las celdas puede parecer inútil para almacenar información, pero si el contenido se lee de forma periódica, la memoria dinámica se comporta de forma idéntica a la estática. Los circuitos de memoria dinámica incluyen la lógica necesaria para que sus celdas sean continuamente leídas independientemente de las operaciones de lectura y escritura realizadas por el procesador, de esta forma se garantiza que su contenido no se pierde. A esta operación se le conoce con el nombre de “refresco”.
La mayoría de ordenadores utilizan memoria dinámica en su memoria principal y las principales razones para ello son el coste y el espacio. La celda de memoria dinámica con un único transistor y un condensador es aproximadamente la cuarta parte del tamaño de la celda de SRAM que consta de alrededor de seis transistores. Pero, además de ser más pequeña, el proceso de diseño de una celda DRAM tiene un coste mucho menor por lo que los chips de memoria de gran capacidad de almacenamiento se diseñan con memoria dinámica.
La memoria estática tiene una clara ventaja frente a la dinámica y es que su tiempo de acceso es menor. En la realidad, en un ordenador se utilizan ambos tipos de memoria. Para aquellos componente en los que se necesite mayor capacidad de almacenamiento la memoria dinámica es la idónea. En aquellos en los que se quiera un tiempo de acceso más reducido se utiliza la memoria estática.
El diseño de un circuito de memoria es significativamente más simple que el de un procesador. La mayor parte del circuito son réplicas de la celda que almacena un bit. Además de estas celdas, las memorias incluyen la lógica necesaria para el refresco (si son DRAM) y para realizar las operaciones de lectura y escritura.
Las dos operaciones que permite una memoria son lectura y escritura. En la operación de lectura, la memoria recibe una dirección y devuelve el byte contenido en el elemento con dicho número. En la operación de escritura la memoria recibe una dirección y un byte y sin devolver resultado alguno sobreescribe el byte en el elemento correspondiente. Otra forma posible de especificar estas operaciones es mediante la notación típica de un lenguaje de programación.
byte Lectura(dirección d): Dada una dirección de memoria
devuelve el byte almacenado en dicho elemento.
void Escritura(dirección d, byte b): Almacena el byte
b en el elemento de dirección d.
El contenido de los datos almacenados inicialmente en la memoria es indefinido. Si al encender el ordenador, la primera operación que se realiza es de lectura sobre memoria RAM, el resultado es indefinido. De esta propiedad se deduce que toda operación de lectura se debe ejecutar sobre una posición de memoria que haya sido previamente escrita. La figura 3.2 muestra el efecto de un conjunto de operaciones sobre memoria.
Al ser la memoria un circuito digital, todos sus datos deben ser codificados igualmente con ceros y unos y esto incluye a los parámetros que reciben las operaciones de lectura y escritura. El dato a leer o escribir es un byte y por tanto ya está codificado en binario. Las direcciones también deben estar codificadas en binario, y como son números naturales (son positivos y comienzan por cero) la codificación utilizada es base dos.
La lectura de un dato consiste en enviar a la memoria los bits que codifican una dirección, y la memoria devuelve ocho bits. La operación de escritura consisten en enviar a la memoria los bits que codifican una dirección y ocho bits de datos, y éstos últimos se almacenan en la posición especificada.
La codificación de las direcciones tiene una relación directa con el tamaño de la memoria. Todo byte en memoria tiene una dirección, y el número de bytes corresponde con el número máximo de dirección que se puede codificar. Al utilizar la codificación en base 2 se deduce que una memoria cuyas direcciones se codifican con n bits puede tener como máximo un tamaño de 2n bytes con direcciones desde 0 hasta 2n-1. En consecuencia, el tamaño T de memoria y el número n de bits que se utilizan para codificar las direcciones están relacionadas por la ecuación
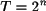
Debido a esta relación entre los bits que codifican una dirección y el número de elementos, las memorias suelen tener un tamaño potencia de 2. El coste de incluir un número determinado de bits hace que se aprovechen todas sus combinaciones.
El tamaño de la memoria se mide en múltiplos que no siguen las reglas convencionales de multiplicación por potencias de 10 sino por potencias de 2. Así, un kilobyte son 210 bytes o 1024 bytes. Las unidades de medida del tamaño de memoria así como sus exponentes y los prefijos de su nomenclatura se muestran en la tabla 3.1.
La conexión entre la memoria y el procesador debe permitir que se realicen las operaciones de lectura y escritura de la forma descrita en la sección 3.2. Para ello son necesarios dos buses. El primero para que la memoria reciba la dirección del procesador, y el segundo para que el procesador envíe a la memoria el dato a escribir o que la memoria envíe al procesador el dato a leer. Además de estos dos buses el procesador debe notificar a la memoria el tipo de operación. La figura 3.3 muestra de forma esquemática cómo están conectadas estas señales.
Dado el número de bits del bus de direcciones se puede deducir el tamaño de la memoria. ¿Se puede cambiar el tamaño de la memoria de un ordenador? A la vista de las conexiones que se muestran en la figura 3.3 esto no es factible. El bus de direcciones es un conjunto de señales fijo y por tanto cambiar el tamaño de memoria significaría cambiar este número. Si un ordenador duplica su memoria RAM necesita un bit adicional en su bus de direcciones.
Los buses se implementan como pistas de metal en un circuito impreso y sus extremos se conectan a los puertos de entrada del procesador y la memoria, por lo que añadir un bit más al bus es una operación extremadamente compleja. Sin embargo, en los equipos actuales sí se ofrece la posibilidad de aumentar la memoria disponible mediante la inserción de circuitos adicionales. Esto es posible porque el bus de direcciones tiene más bits de los que son necesarios y además, el procesador comprueba que las direcciones de memoria utilizadas están dentro del rango correcto.
En general, en un procesador, el número de bits de los que consta el bus de direcciones es un parámetro fundamental de su arquitectura y no puede ser modificado. Por ejemplo, en el procesador Intel Pentium, el bus de direcciones es de 32 bits, con lo que se pueden direccionar hasta un máximo de 4 gigabytes de memoria. En realidad, el procesador puede trabajar con un subconjunto de las direcciones posibles, es lo que se denomina “memoria real” del ordenador frente a la “memoria posible” que representa la memoria máxima que permite direccionar la anchura del bus de direcciones. La figura 3.4 ilustra esta situación para el caso en el que un procesador de tipo Intel Pentium dispone de una memoria real de 256 megabytes.
El procesador incluye un mecanismo por el que el límite de la memoria real es un dato conocido. Antes de realizar cualquier operación sobre memoria se comprueba que la dirección está contenida entre ciertos límites. En caso de que así sea, la operación se realiza, y en caso contrario el procesador detiene el acceso y se produce una excepción en la ejecución.
En el caso concreto del procesador Intel Pentium, el bus de direcciones de 32 bits limita la memoria máxima que puede direccionar a 4 gigabytes. Dada la progresión que ha tenido el precio de la memoria, ordenadores personales que tengan memoria mayor de 4 gigabytes serán pronto una realidad. Un cambio en el bus de direcciones quiere decir una reorganización de la arquitectura entera del procesador, y este ha sido el caso del Intel Pentium. La siguiente generación de procesadores ofrece un bus de direcciones y de datos de 64 bits, por tanto con capacidad para direccionar un máximo de 16 exabytes (264 bytes).
La única estructura que ofrece la memoria es la organización de sus elementos en bytes. Por tanto, para almacenar los datos que manipula un procesador es imprescindible saber de antemano su tamaño. El tamaño de algunos datos básicos viene definido por la arquitectura del propio procesador. Por ejemplo, el lenguaje máquina del Intel Pentium contiene instrucciones máquina para operar enteros de 32 bits. Esto no quiere decir que el procesador no pueda manejar enteros de otros tamaños, sino que el procesador manipula estos de forma mucho más rápida y eficiente. Números de otros tamaños pueden ser manipulados igualmente pero con un coste mayor en tiempo de ejecución.
Los lenguajes de programación de alto nivel como Java definen un conjunto de datos denominados “básicos” y un conjunto de mecanismos para definir datos complejos en base a ellos. Como los programas escritos en estos lenguajes deben ejecutar en diferentes equipos con diferentes procesadores, es difícil definir el tamaño de los datos tal que se ajuste a todos ellos. El compilador se encarga de transformar las operaciones escritas en lenguaje de alto nivel en las instrucciones más adecuadas para manipular los datos en el procesador pertinente. La tabla 3.2 muestra los tipos de datos básicos definidos en Java así como su tamaño.
Tabla 3.2. Tipos de datos básicos en el lenguaje Java
| Tipo | Contiene | Tamaño | Rango |
|---|---|---|---|
| boolean | true, false | 1 bit | |
| byte | Entero | 8 bits | [-128, 127] |
| char | Caracter Unicode | 16 bits | [0, 65535] |
| short | Entero | 16 bits | [-32768, 32767] |
| int | Entero | 32 bits | [-2147483648, 2147483647] |
| long | Entero | 64 bits | [-9223372036854775808, |
| 9223372036854775807] | |||
| float | IEEE-754 Coma Flotante | 32 bits | [±1.4012985E-45, ±3.4028235E+38] |
| double | IEEE-754 Coma Flotante | 64 bits | [±4.94065645841246544E-324, |
| ±1.7976931348623157E+308] |
La regla para almacenar datos en memoria es utilizar tantos bytes como sean necesarios a partir de una dirección de memoria. En adelante, la posición de memoria a partir de la cual está almacenado un dato se denominará su dirección de memoria. De forma análoga, cuando se dice que un dato está en una posición de memoria lo que significa es que está almacenado en esa posición y las siguientes que se precisen.
Los valores booleanos, a pesar de ser los más sencillos, no son los más fáciles de almacenar. La memoria permite el acceso a grupos de 8 bits (1 byte) por lo que almacenar un único bit significa utilizar una parte que no es directamente accesible sino que requiere procesado adicional. Por este motivo se intenta almacenar varios booleanos juntos y de esta forma maximizar la información contenida en un byte. Esta estrategia se utiliza cuando es fácil saber la posición de un booleano dentro del byte. En el caso de que esto no sea posible, se utiliza un byte para almacenar un único bit, con lo que los 7 bits restantes se desperdician. La figura 3.5 muestra estas dos posibles situaciones.
Si un conjunto de 8 booleanos se agrupan para ocupar un byte por
entero, para acceder a un valor concreto se precisan instrucciones
especiales contenidas en prácticamente todos los lenguajes máquina de
los procesadores y suelen estar basadas en instrucciones lógicas tales
como la conjunción o la disyunción. En el caso del Intel Pentium,
mediante operaciones como and u or, la
utilización de máscaras y la consulta de los bits de estado se pueden
manipular los booleanos en un byte.
Tal y como se ha visto en el capítulo 2, la codificación ASCII utiliza 8 bits para representar caracteres. La forma de almacenar estos datos en memoria es simplemente utilizando un elemento o byte para cada letra. La figura 3.6 muestra cómo se almacenan en memoria un conjunto de letras representadas por su valor en ASCII.
Todo símbolo tiene su correspondiente código, incluido el espacio en
blanco (0x20). Si la codificación utilizada fuese Unicode
UTF-16, cada símbolo ocupa dos posiciones consecutivas de memoria en
lugar de una.
Para almacenar un número entero o natural en memoria es imprescindible saber su tamaño en bytes. Las representaciones más utilizadas incluyen tamaños de 2, 4, 8 o hasta 16 bytes. Siguiendo la regla genérica de almacenamiento, se utilizan tantos bytes consecutivos a partir de una posición dada como sean precisos. El tamaño de esta representación no sólo influye en el lugar que ocupan en memoria sino también en el diseño de las partes del procesador que realizan las operaciones. Por ejemplo, si los enteros se representan con 32 bits, el procesador suele incluir una unidad aritmético lógica con operandos de 32 bits.
Pero en esta representación es esencial saber en qué orden se almacenan
estos bytes. Dado un entero que ocupa n bytes a partir de la posición p
de memoria, se pueden almacenar estos bytes comenzando por el byte
menos significativo del número o por el más significativo. Estas dos
posibilidades son igualmente factibles. Considérese el ejemplo de un
procesador que manipula números enteros de 32 bits. La representación
del entero 70960543 en complemento a 2 es 0x043AC59F y se
almacena a partir de la posición de memoria 0x00001000. La
figura 3.7 muestra las dos posibles formas de
almacenamiento dependiendo de si se seleccionan los bytes de menor a
mayor significación o al contrario.
A estas dos formas de almacenar números enteros o naturales de más de un byte en tamaño se les conoce con el nombre de “little endian” y “big endian”. El primero almacena los bytes de menor a mayor significación, mientras el segundo almacena primero el byte de mayor significación.
Cada procesador utiliza un único método de almacenamiento para todos sus enteros o naturales, y en la actualidad coexisten procesadores que utilizan little endian con otros que utilizan big endian.
El problema de la existencia de ambas políticas de almacenamiento surge cuando dos procesadores intercambian números. Como una secuencia de bytes es interpretada de forma diferente por los dos procesadores, se debe realizar un proceso de traducción por el que se garantiza que ambos manipulan los mismos datos. La figura 3.8 muestra cómo la interpretación de un número de 4 bytes con ambas formas ofrece resultados diferentes.
Existen numerosos argumentos a favor y en contra de ambas notaciones pero ninguno de ellos es concluyente. Quizás el más intuitivo a favor de la notación little endian es que si un número se almacena siguiendo este esquema y su representación se extiende en tamaño, únicamente es necesario utilizar más posiciones de memoria sin reorganizar los bytes. En cambio, en el caso de big endian, la misma operación requiere almacenar los bytes en diferentes posiciones de memoria.
El almacenamiento de instrucciones consiste simplemente en utilizar posiciones consecutivas de memoria para almacenar los bytes de la codificación de cada una de ellas. Una secuencia de instrucciones, por tanto, requiere tantas posiciones de memoria como la suma de los tamaños de cada una de las codificaciones.
Tal y como se ha descrito en la sección 2.8.2, existen dos tipos de lenguajes máquina. Los procesadores con formato fijo de instrucción almacenan las instrucciones en memoria en porciones idénticas. En este caso, dada una porción de memoria que contiene una secuencia de instrucciones es muy fácil acceder a una de ellas de forma arbitraria, pues todas ocupan lo mismo. El caso de instrucciones de formato variable es ligeramente más complejo. Dada una porción de memoria, para saber qué posiciones ocupa cada instrucción es preciso interpretar la información que éstas codifican. Esto es precisamente lo que hace el procesador al comienzo de la ejecución de cada instrucción, solicita de memoria tantos bytes como sean necesarios para obtener toda la información referente a la instrucción. Una vez concluida esta fase, la siguiente instrucción comienza en la posición contigua de memoria. La figura 3.9 muestra un ejemplo de cómo se almacenan los dos posibles formatos de instrucción.
En el almacenamiento de instrucciones no es preciso distinguir entre los estilos big endian o little endian pues en la codificación no existen bytes más significativos que otros. El convenio que se utiliza es que se escriben los bytes de la instrucción en el mismo orden en el que están almacenados en memoria.
La memoria almacena un byte en cada una de sus posiciones que a su vez tiene una dirección única. El funcionamiento de la memoria está totalmente definido mediante esta estructura. Sin embargo, cuando la memoria forma parte del conjunto de un ordenador, el tiempo que tarda en realizar una operación es mucho mayor comparado con el que tarda el procesador en ejecutar una instrucción. En otras palabras, los accesos a memoria requieren tanto tiempo que retrasan la ejecución de las instrucciones del procesador.
Existen múltiples decisiones de diseño en la arquitectura de un procesador que se utilizan para paliar este retraso. De entre ellas, una de las más efectivas es realizar las operaciones en memoria en paquetes de información mayores de un byte. Es decir, cuando el procesador lee y escribe en memoria, en lugar de trabajar con un único byte, los datos están compuestos por más de un byte en posiciones consecutivas. Esta técnica tiene la ventaja de que un único acceso a memoria para, por ejemplo, lectura, proporciona más de un byte en posiciones consecutivas. El inconveniente es que es posible que en ciertas ocasiones, se obtenga de memoria más información de la estrictamente necesaria.
Generalmente, todo procesador ofrece la posibilidad de escribir un cierto tamaño de datos en bytes (mayor que uno) en una única operación de memoria. La forma en que se implementa este mecanismo es utilizando múltiples módulos de memoria. Por ejemplo, supóngase que se quiere manipular la memoria tal que las operaciones se hagan en grupos de cuatro bytes simultáneamente. El ejemplo que se describe a continuación se puede realizar con cualquier agrupamiento de información que sea potencia de dos.
La primera decisión es almacenar los datos en cuatro módulos o circuitos independientes de memoria de tal forma que la posición 0 de memoria se almacena en el primer módulo, la posición 1 en el segundo, y así sucesivamente. La quinta posición de memoria se almacena de nuevo en el primer módulo.
Con este esquema, el módulo en el que está almacenado el dato de la posición p se obtiene mediante la expresión p % 4. La consecuencia de este patrón de almacenamiento es que se puede acceder a cuatro bytes de memoria en el tiempo en el que se lee un byte. Dada una dirección de memoria, cada módulo devuelve un byte y se obtienen los cuatro en el tiempo de retardo de un único módulo pues todos trabajan en paralelo. Por tanto, dada una dirección de memoria d, con esta técnica, la memoria es capaz de devolver los datos desde la posición d / 4 (donde esta división es división entera) a la posición d / 4 + 3 en el tiempo de retardo de un único módulo.
Otra interpretación de esta organización es que la memoria contiene grupos de 4 bytes y cada uno de ellos está almacenado en la posición d / 4. Pero, dada la dirección d, ¿como se obtiene el número d / 4?. La dirección de memoria está codificada en base 2, y como esta operación es una división por una potencia de la base, equivale a tomar la dirección ignorando los dos bits de menos peso, pues 4 = 22. En realidad, dada la dirección d el cociente de la división entera entre cuatro es el número de grupo mientras que el resto de esta división representa el byte del grupo de 4 al que se refiere d. La figura 3.10 muestra cómo implementar este esquema de acceso en una memoria con direcciones de 32 bits.
Cada módulo de memoria recibe 30 de los 32 bits de la dirección. Esto es así porque la memoria consta de exactamente 230 grupos de cuatro bytes y cada módulo de memoria provee un byte de cada grupo. Con esta configuración se obtienen cuatro bytes en el tiempo en el que un módulo lee uno de sus bytes, pues los cuatro acceden a su dato respectivo de forma paralela. Además de los componentes que se muestran en la figura 3.10, la nueva memoria contiene la lógica necesaria para igualmente permitir la lectura y escritura de un único byte en lugar de cuatro.
Los accesos a esta memoria a direcciones que son múltiplos de 4 se denominan accesos alineados. Pero, ¿qué sucede si el procesador quiere acceder a 4 bytes consecutivos de esta memoria pero que no comienzan en una posición múltiplo de 4? El paralelismo se obtiene porque si cada módulo lee la misma dirección de memoria y ofrece su correspondiente byte, pero si el procesador requiere cuatro bytes que no están en el mismo grupo, este esquema no funciona puesto que no todos los módulos deben leer de la misma dirección. A este tipo de accesos se le denominan accesos no alineados. En tal caso, la memoria se ocupa internamente de realizar cuantos accesos sean necesarios para devolver los cuatro bytes que requiere el procesador. No se precisan más de dos accesos a memoria para servir cualquier petición de cuatro bytes consecutivos del procesador. Por ejemplo, si el procesador requiere los datos en las posiciones 4 * d + 3 a 4 * d + 6, el procesador selecciona el último byte del grupo con dirección 4 * d y los tres primeros del grupo con dirección 4 * (d + 1). La figura 3.11 muestra los dos accesos a memoria para obtener los datos requeridos.
En el caso concreto del procesador Intel Pentium, su arquitectura define su su bus de direcciones y su bus de datos ambos de tamaño 32 bits. El procesador puede leer o escribir 4 bytes de datos en memoria de forma simultánea.
En la sección 3.4 se ha visto cómo los tipos de
datos básicos se almacenan en memoria, pero los programas manipulan
estructuras de datos más complejas compuestas a su vez por datos
básicos. Un ejemplo de estas estructuras son las tablas o
arrays. Una tabla es un conjunto de datos
agrupados de forma que cada uno de ellos puede ser accedido a través de
un índice que se corresponde con un número natural. El primer elemento
está en la posición con índice cero y el último en la posición con índice
igual al número de elementos de la tabla menos uno. En los lenguajes de
programación tales como C o Java, si una tabla de elementos se denomina
tabla, el elemento en la posición i se accede
mediante la expresión tabla[i]. ¿Cómo se almacenan estos
datos en memoria de forma que puedan ser accedidos por el procesador?
Al igual que en el caso de los datos básicos, la estrategia consiste en utilizar posiciones consecutivas de memoria para almacenar los elementos. Si una tabla contiene n elementos y cada uno de ellos se codifica con m bytes, el espacio total ocupado por la tabla es de n * m bytes. Dada la dirección de memoria d a partir de la cual se almacena la tabla y el tamaño m en bytes de cada elemento la dirección donde está almacenado el elemento en la posición p se obtiene sumando a d los bytes que ocupan los elementos anteriores, o lo que es lo mismo d + (p * m). La figura 3.12 ilustra cómo se realiza este cálculo.
Considérese, por ejemplo, una tabla de 4 enteros almacenada en la memoria
del procesador Intel Pentium a partir de la posición 0x100 y
con los números 0x34AF89C4, 0x583B7AF1,
0x97FA7C7E, 0x14C8B9A0 almacenados en ese mismo
orden. La figura 3.13 muestra su disposición en memoria.
Pero para manipular tablas de datos no sólo basta con almacenar los elementos en posiciones consecutivas. Considérese el siguiente ejemplo. Se dispone de una tabla de enteros y se debe calcular la suma total de sus elementos. Para ello se comienza sumando el primer elemento, a él se le suma el segundo, a este resultado el tercero, y así sucesivamente. Pero ¿cómo se sabe que se ha llegado al último elemento? Para cualquier tabla, además de la dirección de comienzo y el tamaño de sus elementos, es preciso saber el número de elementos que contiene.
Existen dos mecanismos para saber cuántos elementos contiene una tabla. El primero de ellos consiste en depositar como último elemento, un valor que denote el final. Por ejemplo, considérese una tabla de letras que almacena una frase. Cada letra se almacena con su codificación en ASCII (ver sección 2.8.1), por lo que cada letra ocupa un byte. Al final de la tabla se incluye un byte con valor 0 que está reservado específicamente en ASCII para codificar el final de una secuencia de letras. Para recorrer todos los elementos de esta tabla basta con escribir un bucle que se detenga cuando encuentre el valor cero.
Pero la técnica de depositar un valor concreto como último elemento no funciona para todos los tipos de datos. ¿Qué sucede en el caso de una tabla de números enteros? Cada elemento se codifica con su representación en complemento a 2 que utiliza la totalidad de posibles combinaciones de bits. Por tanto, no es posible utilizar un valor específico para denotar el final de la tabla pues se confundiría con la representación de su número entero correspondiente. Para saber el tamaño, simplemente hay que almacenar este valor en una posición adicional de memoria. De esta forma, si se desea acceder a todos los elementos de la tabla de forma secuencial basta con escribir un bucle que compare la posición del elemento con el tamaño. Tanto esta técnica como la anterior se utilizan de forma frecuente en los lenguajes de programación de alto nivel.
El lenguaje de programación Java garantiza que el acceso a los elementos de un array se realiza siempre con un índice correcto. Dado que toda tabla en Java tiene su primer elemento en la posición con índice cero, el índice i con el que se accede a una tabla de n elementos debe cumplir 0 ≤ i < n.
Pero esta comprobación sólo se puede realizar mientras un programa está
en ejecución. Supóngase que un programa Java contiene la expresión
tabla[expresión]. ¿Cómo se puede garantizar que el acceso
a la tabla es correcto? La solución consiste en que antes de que el
programa ejecute esta expresión se comprueba que su valor está en los
límites correctos, en cuyo caso el acceso se realiza sin problemas. Si
el índice no está entre los límites permitidos el programa produce una
excepción del tipo ArrayIndexOutOfBounds.
Para implementar este mecanismo no sólo toda tabla en Java debe tener almacenado su tamaño sino que cada acceso va precedido de la comprobación del valor del índice. Se necesita, por tanto, un mecanismo que almacene los datos de una tabla y su tamaño de forma compacta y que además permita una eficiente comprobación de los accesos a sus elementos.
La solución en Java consiste en almacenar el tamaño de una tabla junto
con sus elementos en posiciones consecutivas de memoria. De entre todas
las posibilidades de organizar estos datos, la más lógica es poner el
tamaño en las primeras posiciones de memoria seguido de los
elementos. La figura 3.14 muestra cómo se
almacena en memoria una tabla de seis enteros de 32 bits en formato
little endian a partir de la posición
0x100.
Antes de cada acceso al elemento i que ocupa t bytes de una tabla con s elementos almacenada a partir de la posición d, el programa escrito en Java realiza las siguientes operaciones:
Obtiene el entero s almacenado a partir de la posición d.
Comprueba que 0 ≤ i. En caso de que no sea así produce una excepción.
Comprueba que i < s. En caso de que no sea así produce una excepción.
Calcula la dirección donde está el elemento i como d + 4 + (t * i).
Supongamos que la memoria utilizada tiene un tamaño de 4 Gigabytes y por tanto sus direcciones se representan con 32 bits. Las direcciones de memoria son números naturales en el rango [0, 232 - 1]. Pero este número natural es susceptible de ser almacenado él mismo en memoria. Es decir, se puede almacenar la representación binaria de una dirección de memoria en la propia memoria. Al tener un tamaño de 32 bits o 4 bytes, se utilizan para ello cuatro posiciones de memoria consecutivas.
Una dirección de memoria, por tanto, se puede considerar de dos formas
posibles: o como una dirección de una celda de memoria, o como un número
natural susceptible de ser manipulado como tal. Supóngase que en la
posición de memoria 0x00000100 se encuentra almacenado el
número entero de 32 bits 0x0153F2AB y que en la posición
0x00000200 se debe almacenar la dirección de dicho
número. Para ello se almacena, a partir de la posición
0x00000200 el número 0x00000100 utilizando los
cuatro bytes a partir de esa posición y se hace en orden creciente de
significación al utilizar el esquema little
endian. El resultado se ilustra en la figura 3.15.
Tras almacenar la dirección de memoria de un dato en la posición
0x00000200, ¿es posible obtener de nuevo el número
0x0153F2AB? La respuesta es afirmativa, pero no de forma
inmediata, se debe obtener de memoria primero los cuatro bytes
almacenados en la posición 0x00000200 y utilizarlos como una
dirección de memoria de donde obtener los cuatro bytes contenidos en la
posición 0x00000100. El acceso a este último dato se ha
realizado de forma indirecta, es decir, mediante un acceso previo a
memoria para obtener la dirección del dato final. Utilizando la notación
funcional de operaciones sobre memoria, el acceso al dato se logra
ejecutando Lectura(Lectura(0x00000200)).
A este mecanismo de acceso a un dato en memoria a través de su dirección
a su vez almacenada en otra posición se le conoce con el nombre de
“indirección”. En el ejemplo anterior se dice que el
dato almacenado en la posición 0x00000200 apunta al dato
0x0153F2AB. La figura 3.16 ilustra
esta situación.
El mecanismo de indirección se puede encadenar de manera arbitrariamente
larga. La dirección que contiene la dirección de un dato, a su vez se
puede almacenar de nuevo en memoria. En tal caso, para acceder al dato
final se requieren dos accesos a memoria en lugar de uno. Por tanto, es
posible almacenar las direcciones tal que haya que seguir una cadena de
indirecciones para en última instancia acceder al dato. La figura 3.17 muestra una distribución de datos
tal que la posición 0x00000100 contiene “la dirección
de memoria de la dirección de memoria de la dirección de memoria del
dato”.
De la técnica de indirección se deriva que en memoria no sólo se almacenan datos (naturales, enteros, coma flotante, letras, etc.) sino también direcciones de memoria. Todos estos datos, a efectos de almacenamiento y su manipulación por el procesador, no son más que una secuencia de bytes en diferentes celdas. El que una secuencia de bits determinada se interprete como un número o como una dirección queda totalmente bajo el control del programador. En los programas escritos en ensamblador es preciso saber qué dato está almacenado en qué posición de memoria pero el propio lenguaje no aporta mecanismo alguno que compruebe que se el acceso se hace de forma correcta. Si por error en un programa se obtiene un dato de 32 bits de memoria y se interpreta como una dirección cuando en realidad es un dato numérico o viceversa, lo más probable es que el programa termine de forma brusca o con resultados incorrectos.
El almacenar una dirección en memoria no parece a primera vista un mecanismo útil, pues esta cumple un único papel que es el de apuntar al dato en cuestión. Sin embargo, esta técnica se utiliza con frecuencia en la ejecución de programas.
Ejemplo 3.1. Almacenamiento de una tabla de strings
Supóngase que se dispone de un conjunto de n strings almacenados en otras tantas posiciones de memoria. Aunque las letras de cada string están almacenadas en posiciones consecutivas, los strings no están uno a continuación de otro sino en zonas de memoria dispersas. Se quiere imprimir estos strings en orden alfabético. El primer paso es ordenar los strings para a continuación imprimir cada uno de ellos por orden.
Para ordenar los strings hay dos opciones, o se manipulan todos los caracteres de cada uno de ellos, o se manipulan sus direcciones de comienzo. Es decir, en lugar de tener los strings ordenados alfabéticamente y almacenados en posiciones consecutivas de memoria, se almacenan por orden las direcciones de memoria de comienzo de cada string y se ordenan en base a las letras que contienen. Esta estructura se ilustra en la figura 3.18.
La ordenación los strings se puede realizar sin mover ninguna de las letras en memoria. La tabla resultante contiene en cada uno de sus elementos una indirección a un string, es decir, la dirección en la que se encuentra el string pertinente. Para imprimir los strings en orden alfabético se itera sobre los elementos de la tabla y mediante doble indirección se accede a las letras de cada string.
Ejemplo 3.2. Referencias en el lenguaje Java
El lenguaje de programación Java utiliza el mecanismo de indirección
para acceder a los datos almacenados en un objeto. Supóngase que se
ha definido una clase con nombre Dato que a su vez
contiene un campo de acceso público, entero y con nombre
valor. Se ejecuta la siguiente porción de código.
| Línea | Código |
|---|---|
1 2 3 4 5 6 |
Dato obj1, obj2;
obj1 = new Dato();
obj1.valor = 3;
obj2 = obj1;
obj2.valor = 4;
System.out.println(obj1.valor)
|
¿Qué valor imprime por pantalla la última línea? El código asigna al
campo valor de obj1 el valor 3, a
continuación se produce la asignación obj2 = obj1, luego
se asigna el valor 4 al campo valor de obj2
y se imprime el mismo campo pero de obj1. Al ejecutar
este fragmento de código se imprime el valor 4 por pantalla. La línea
que explica este comportamiento es la asignación obj2 =
obj1. En Java, todo objeto se manipula a través de una
“referencia”. Las variables obj1 y
obj2 son referencias y la asignación obj1 =
obj2 no transfiere el contenido entero de un objeto a otro,
sino que se transfiere el valor de la referencia. Por tanto, al
ejecutar esta asignación, obj2 se refiere al mismo
objeto que obj1 y por eso la última línea imprime el
valor 4.
El mecanismo interno que se utiliza a nivel de lenguaje máquina para
representar las referencias está basado en el concepto de
indirección. Cuando se crea un objeto se almacenan sus datos en
memoria. Cuando un objeto se asigna a una referencia esta pasa a
contener la dirección de memoria a partir de la cual está
almacenado. La asignación obj2 = obj1 transfiere la
dirección de memoria contenida en obj1 al contenido de
obj2. Cualquier modificación que se haga a través de la
referencia obj1 afecta por tanto al objeto al que apunta
obj2 pues ambas referencias apuntan al mismo objeto. La
figura 3.19 ilustra cómo se asignan los valores en memoria
para este ejemplo.
El objeto está ubicado en una posición arbitraria de memoria (en la
figura 3.19 es la posición
0x00000100). En dos posiciones de memoria adicionales se
almacenan las referencias obj1 y obj2. La
primera de ellas recibe su valor al ejecutarse el constructor de la
clase. La segunda recibe el mismo valor cuando se ejecuta la
asignación. A partir de este momento, cualquier modificación
realizada en el objeto a través de obj1 será visible si
se consulta a través de obj2.
Ejemplo 3.3. Doble indirección con referencias en el lenguaje Java
Las referencias en Java se utilizan, por tanto, como indirecciones a
memoria. Pero las clases definidas en Java pueden contener en su
interior campos que sean referencias a otros objetos. Por ejemplo, si
se define una segunda clase Dato2 en cuyo interior
existe un campo con nombre c1 de la clase
Dato, este campo es una referencia a un
objeto. Supóngase que se ejecuta la siguiente porción de código.
En este caso la referencia obj2 apunta a un objeto de la
clase Dato2 que a su vez contiene en su interior una
referencia a un objeto de la clase Dato. Para ejecutar
la última línea en la que se asigna el valor 4 al campo
valor es preciso realizar una doble indirección. La
referencia obj2 contiene la dirección del objeto de la
clase Dato2, y este a su vez contiene en su interior una
referencia que contiene la dirección del objeto de la clase
Dato. Tras esta doble indirección se asigna el valor 4 a
dicho dato. La figura 3.20 muestra
el acceso a este dato a través de la doble indirección.
Diseñar una memoria tal que ofrezca al procesador la capacidad de acceder a ocho bytes consecutivos de memoria en el tiempo en el que se lee un único byte. El diseño debe incluir el tamaño de los buses así como su estructura interna.
La memoria de un procesador ofrece acceso a cuatro bytes consecutivos de memoria mediante un único acceso siempre y cuando estén almacenados a partir de una posición que es múltiplo de cuatro. En este procesador se ejecutan dos programas con idénticas instrucciones que acceden a un array de un millón de enteros de tamaño 32 bits. El primer programa realiza un total de un millón de accesos a la zona de memoria en la que está almacenado el array. El segundo programa realiza exactamente el doble de accesos a memoria a la misma zona, ¿cómo es esto posible?
Supongamos un procesador que permite operaciones en memoria en bloques de 32 bits (4 bytes). Se ejecutan las siguientes instrucciones:
Write(0x100, 0x01234567)
Write(0x101, 0x89ABCDEF)
Write(0x102, 0xFFFFFFFF)
Read(0x100)
¿Cuál es el resultado de la última operación?
Una tabla en Java almacena referencias a objetos. Estas referencias
ocupan 32 bits cada una. La tabla contiene 23 elementos y está
almacenada a partir de la posición 300 de memoria. ¿En qué dirección
está almacenada la referencia del elemento en tabla[21]?
¿Y la referencia del elemento tabla[23]?
¿Cuántas posiciones de memoria reserva la ejecución de la expresión
Java int[] tabla = new int[49]?
Supongase un ordenador con memoria principal de 16 Kilobytes (1 Kilobyte = 1024 bytes). Explicar cuantos bits de datos y dirección se precisan y por qué en los siguientes supuestos:
La memoria lee y escribe la información en grupos de 8 bits:
La memoria lee y escribe la información en grupos de 32 bits: